2. Система случайных величин. Функция и плотность распределения вероятностей для системы случайных величин.
Функция распределения системы двух случайных величин:
Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х<х и У<у: F(x,y)=P((X<x)(Y<y)).
Функцией распределения системы n случайных величин (X1,Х2, ..., Хn) называется вероятность совместного выполнения n неравенств вида Xi < xi:
F(x1,x2,…,xn)=P((X1<x1) (X2<x2)… (Xn<xn))
Свойства функции распределения системы случайных величин:
Функция распределения F(x, у) есть неубывающая функция обоих своих аргументов, т.е. при и
Повсюду на -∞ функция распределения равна нулю: F(-∞,y)=F(x,-∞)=0.
При одном из аргументов, равном +∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
F(x,+∞)=F1(x) , F(+∞, y)=F2(y), где F1(x), F2(y) — соответственно функции распределения случайных величин X и Y.
Если оба аргумента равны +∞, функция распределения системы равна единице: F(+∞,+∞)=1.
Плотностью распределения системы n непрерывных случайных величин называется n-я смешанная частная производная функции F(x1,x2,…,xn), взятая один раз по каждому аргументу:
Свойства плотности распределения системы случайных величин:
Плотность распределения системы есть функция неотрицательная:
>=0.интеграл в бесконечных пределах от плотности распределения системы равен единице:
Задача 11.10
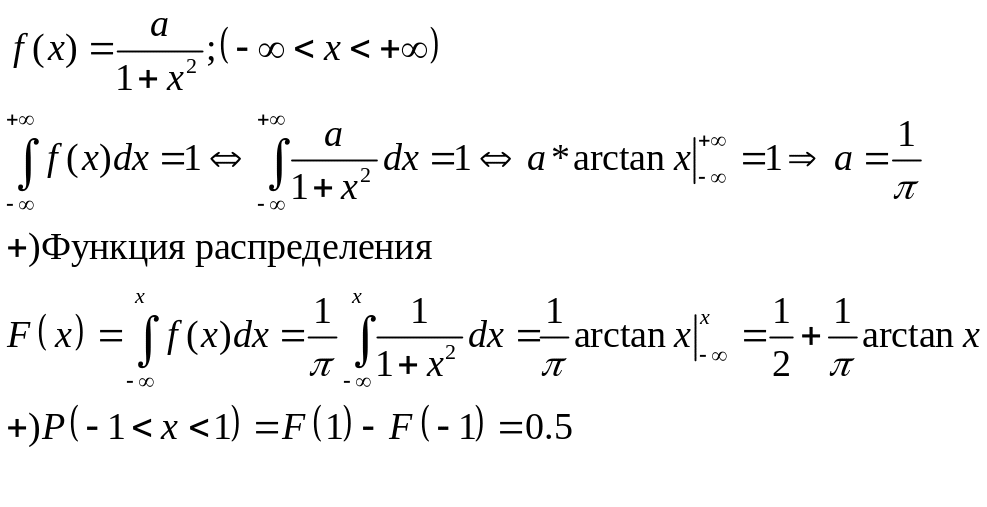
Экзаменационный Билет №32
1. Случайная величина. Функция и плотность распределения вероятностей для случайных величин.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.
Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.
Сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятность каким-то образом распределена между отдельными значениями.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
Такую таблицу мы будем называть рядом распределения случайной величины X.
Многоугольник распределения
Функция распределения — самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных.
Эта функция обозначается F(x): F(x)=P(X<x).
Некоторые общие свойства функции распределения.
Функция распределения F(x) есть неубывающая функция своего аргумента, т. е. при.
На минус бесконечности функция распределения равна нулю: F (-∞) = 0.
На плюс бесконечности функция распределения равна единице: F (∞) = 0.
График функции распределения F (х) в общем случае представляет собой график неубывающей функции (рис. 5.2.2), значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрывы).
Действительно
Плотность распределения:
Пусть имеется непрерывная случайная величина X с функцией распределения F(x), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от х до х+Δх:
Р (х < X < х + Δx) = F (х + Δх) — F (х).
Рассмотрим среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать Δx к нулю. В пределе получим производную от функции распределения:
Функция f(х)=F’(x) - производная функции распределения - называется плотностью распределения непрерывной случайной величины X. Она существует только для непрерывных случайных величин.
Иногда функцию f(x) называют также «дифференциальной функцией распределения» или «дифференциальным законом распределения» величины X.
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.
Выразим вероятность попадания величины X на отрезок от α до β через плотность распределения:
О сновные свойства плотности распределения.
Плотность распределения есть неотрицательная функция:
Интеграл в бесконечных пределах от плотности распределения равен единице:
2. Поглощающие цепи Маркова.
Задача 29.10
Экзаменационный Билет №33
1. Регулярные цепи Маркова.
2. Система случайных величин. Функция и плотность распределения вероятностей для системы случайных величин.
Функция распределения системы двух случайных величин:
Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х<х и У<у: F(x,y)=P((X<x)(Y<y)).
Функцией распределения системы n случайных величин (X1,Х2, ..., Хn) называется вероятность совместного выполнения n неравенств вида Xi < xi:
F(x1,x2,…,xn)=P((X1<x1) (X2<x2)… (Xn<xn))
Свойства функции распределения системы случайных величин:
Функция распределения F(x, у) есть неубывающая функция обоих своих аргументов, т.е. при и
Повсюду на -∞ функция распределения равна нулю: F(-∞,y)=F(x,-∞)=0.
При одном из аргументов, равном +∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
F(x,+∞)=F1(x) , F(+∞, y)=F2(y), где F1(x), F2(y) — соответственно функции распределения случайных величин X и Y.
Если оба аргумента равны +∞, функция распределения системы равна единице: F(+∞,+∞)=1.
Плотностью распределения системы n непрерывных случайных величин называется n-я смешанная частная производная функции F(x1,x2,…,xn), взятая один раз по каждому аргументу:
Свойства плотности распределения системы случайных величин:
Плотность распределения системы есть функция неотрицательная: >=0.
интеграл в бесконечных пределах от плотности распределения системы равен единице:
Задача 30.7
Экзаменационный Билет №34
1. Группированный статистический ряд. Выравнивание опытных данных.
2. Система случайных величин. Функция и плотность распределения вероятностей для системы случайных величин.
Функция распределения системы двух случайных величин:
Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х<х и У<у: F(x,y)=P((X<x)(Y<y)).
Функцией распределения системы n случайных величин (X1,Х2, ..., Хn) называется вероятность совместного выполнения n неравенств вида Xi < xi:
F(x1,x2,…,xn)=P((X1<x1) (X2<x2)… (Xn<xn))
Свойства функции распределения системы случайных величин:
Функция распределения F(x, у) есть неубывающая функция обоих своих аргументов, т.е. при и
Повсюду на -∞ функция распределения равна нулю: F(-∞,y)=F(x,-∞)=0.
При одном из аргументов, равном +∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
F(x,+∞)=F1(x) , F(+∞, y)=F2(y), где F1(x), F2(y) — соответственно функции распределения случайных величин X и Y.
Если оба аргумента равны +∞, функция распределения системы равна единице: F(+∞,+∞)=1.
Плотностью распределения системы n непрерывных случайных величин называется n-я смешанная частная производная функции F(x1,x2,…,xn), взятая один раз по каждому аргументу:
Свойства плотности распределения системы случайных величин:
Плотность распределения системы есть функция неотрицательная: >=0.
интеграл в бесконечных пределах от плотности распределения системы равен единице:
Задача 30.1
Экзаменационный Билет №35
1. Критерий согласия Пирсона. Проверка правдоподобия гипотез.
2. Применение центральной предельной теоремы.
а) Пусть — независимые случайные величины с математическими ожиданиями и дисперсиями
Предположим, что условия центральной предельной теоремы выполнены и число слагаемых п достаточно для того, чтобы закон распределения величины можно было считать приближенно нормальным.
Тогда вероятность того, что случайная случайная величина У попадает в пределы участка , выражается фопмулой
Где математическое ожидание и среднее квадратическое отклонение величины V,
Ф* — нормальная функция распределения.
b) Частным случаем центральной предельной теоремы для дискретьых случайных величин является теорема Лапласа.
Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение
где Y — число появлений события А в n опытах, q = l — р.
Задача 18.16
Экзаменационный Билет №36
1. Оценка числовых характеристик по неполным данным.
2. Числовые характеристики системы 2-х случайных величин
Начальным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения Хk на Ys:
αk, s=M[XkYs]
Центральным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин:
µk, s=
где,
Для прерывных случайных величин:
,
где pij = P((X=xi)(Y=yj)) - вероятность того, что система (X, Y) примет значения (xi, yj), а суммирование распространяется по всем возможным значениям случайных величин X, Y.
Для непрерывных случайных величин:
Mатематические ожидания величин X и У, входящих в систему:
mx= α1,0 = M[X1Y0] = M[X]
mx= α0,1 = M[X0Y1] = M[Y]
Дисперсии величин X и У: Dx = µ2, 0= =
Dy = µ0, 2= =
Характеристика Кxy называется корреляционным моментом:
Для прерывных случайных величин:
Для непрерывных случайных величин:
Для независимых случайных величин корреляционный момент равен нулю.
Характеристика называется коэффициентом корреляции величин X и Y:
, где - средние квадратические отклонения величин X, Y.
Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать по линейному закону. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами.
Если случайные величины X а У связаны точной линейной функциональной зависимостью: Y=aX+b, то | | = 1.