3. Задача 31.10

Экзаменационный Билет №28

1.Числовые характеристики случайных функций.

Рассмотрим сечение случайной функции X (t) при фиксированном t.

Математическим ожиданием случайной функции X(t) называется неслучайная функция m_x(t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.

m_x(t) = M{X(t)}

Дисперсией случайной функции X (t) называется неслучайная функция D_x(t), значение которой для каждого t равно дисперсии соответствующего сечения случайной функции:

D_x(t) = D{X(t)}

Среднее квадратическое отклонение случайной функции:

σ_x(t) =

Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящимися к различным t.

Корреляционной функцией случайной функции X(t) называется неслучайная функция двух аргументов K_x(t, t’), которая при каждой паре значений t, t’ равна корреляционному моменту соответствующих сечений случайной функции:

K_y(t, t’) = M[ (t) (t’)]

Где, (t) = X(t) – m_x(t); (t’) = X(t’) – m_x(t’);

Пологая t = t’  K_y(t, t’) = M[( (t))²] = D_x(t)

K_y(t, t’) = K_y(t’, t)

Вместо корреляционной функции Kx(t, t') можно пользоваться нормированной корреляционной функцией:

При t'=t нормированная корреляционная функция равна единице:

Неслучайная функция p(t):

• Y(t) = X(t) + p(t)  m_y(t) = m_x(t) + p(t); K_y(t, t’) = K_x(t, t’)

• Y(t) = p(t)X(t)  m_y(t) =m_x(t)*p(t); K_y(t, t’) = p(t)p(t’)K_x(t, t’)

Нормированной называется случайная функция вида:

Корреляционная функция нормированной случайной функции X_N(t) равна

2.Линейные преобразования случайных функций.

Пусть на вход линейной системы с оператором L воздействует случайная функция X (t), причем известны ее характеристики: математическое ожидание m_x(t) и корреляционная функция K_x(t, t'). Реакция системы представляет собой случайную функцию Y(t) = L(X(t)).

Требуется найти характеристики случайной функции Y(t) на выходе системы: my(t) и Ky(t, t'). Короче: по характеристикам случайной функции на входе линейной системы найти характеристики случайной функции на выходе.

Покажем сначала, что можно ограничиться решением этой задачи только для однородного оператора L. Действительно, пусть оператор L неоднороден и выражается формулой:

L(X(t)) = L₀(X(t))+ρ(t).

где L₀—линейный однородный оператор, ρ(t)— определенная неслучайная функция. Тогда

m_y(t) = M[L₀{X(t)}] + ρ(t).

т. е. функция ρ(t) просто прибавляется к математическому ожиданию случайной функции на выходе линейной системы. Что же касается корреляционной функции, то, как известно, она не меняется от прибавления к случайной функции неслучайного слагаемого.

Поэтому в дальнейшем изложении под «линейными операторами» будем разуметь только линейные однородные операторы.

Решим задачу об определении характеристик на выходе линейной системы сначала для некоторых частных видов линейных операторов.

3. Задача 32.11

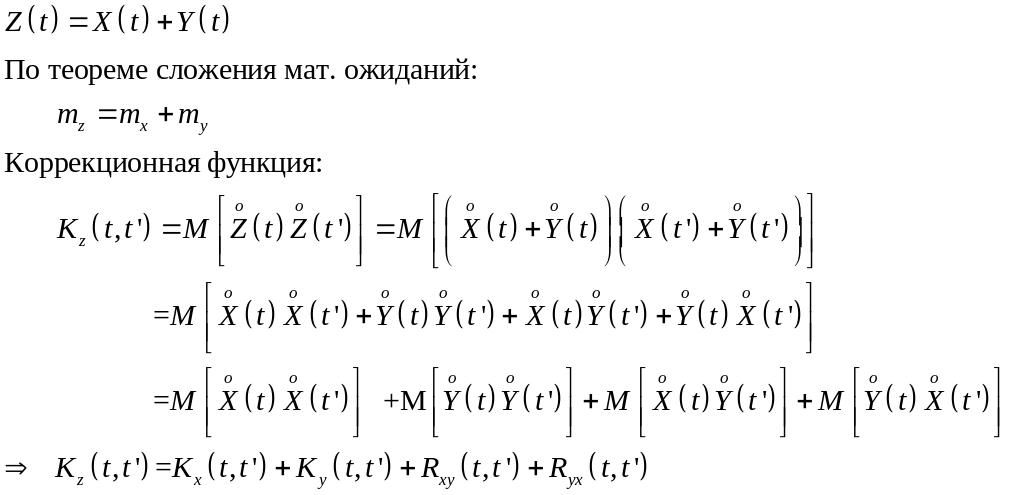
Экзаменационный Билет №29

1.Теорема умножения вероятностей.

Событие А называется зависимым(независимым) от события В, если вероятность события А (не) зависит от того, произошло событие В или нет.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А|В).

Условие независимости события А от события В можно записать в виде: Р(А|В) = Р(А), а условие зависимости в виде: Р(А|В) ≠ Р(А).

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

P(AB) = Р(А)*Р(В\А) = P(B)*P(A\B).