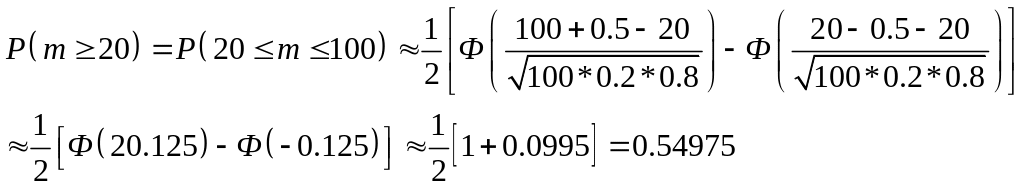Contents

Экзаменационный билет №1 5

1- Основные понятия теории вероятности. 5

2- Центральная предельная теорема. Различные формы центральной предельной теоремы 6

3- Задача 30.3 (а). 7

экзаменационный билет №2 7

1. Классическая, частотная, геометрическая схема вычисления вероятности. 7

2.Неравенство Чебышева. Две формы неравенства Чебышева. 7

3. Задача 30.3. (б) 8

Экзаменационный Билет №3 9

1.Теорема сложения вероятностей. 9

2.Полиномиальное распределение вероятностей (второе обобщение схемы независимых испытаний). 9

3. Задача 30.3 (в ) 10

Экзаменационный Билет №4 10

1.Теорема умножения вероятностей. 10

2.Два примера применения центральной предельной теоремы. 10

3. Задача 29.6 11

Экзаменационный Билет №5 11

1.Независимые и зависимые события. 11

2.Следствия закона больших чисел: теорема Бернулли и Пуассона. 12

3. Задача 29.9 (а). 12

Экзаменационный Билет №6 12

1.Формула полной вероятности 12

2.Понятие об усиленном законе больших чисел. 13

3. Задача 15.3. 13

Экзаменационный Билет №7 14

1.Формула Байеса. 14

2.Закон больших чисел для зависимых случайных величин. 14

3. Задача 15.4. 14

Экзаменационный Билет №8 15

1.Схема независимых испытаний. Биномиальное распределение. 15

2. Теорема Пуассона, как одна из форм закона больших чисел. 15

3.Задача 13.9. 15

Экзаменационный Билет №9 15

1.Обобщение схемы независимых испытаний. Локальная теорема Муавра – Лапласа. 15

2.Теорема Бернулли, как одна из форм закона больших чисел. 16

3. Задача 13.1 (а,б). 17

Экзаменационный Билет №10 17

1.Функции распределения случайных величин. 17

2.Закон больших чисел в форме теоремы Чебышева. 17

3. Задача 10.3. 18

Экзаменационный Билет №11 18

1. Плотность распределения случайных величин. 18

2. Неравенство Чебышева. 19

3.Задача 12.3. 20

Экзаменационный Билет №12 20

1.Числовые характеристики случайных величин. Характеристики положения. 20

2.Закон больших чисел. 21

3. Задача 12.10. 22

Экзаменационный Билет №13 22

1.Числовые характеристики случайных величин. Моменты. Характеристики рассеивания. 22

2.Понятие о стационарных случайных функциях в широком смысле. 23

3. Задача 10.5. 23

Экзаменационный Билет №14 23

1.Биномиальный ЗРВ случайных величин, его числовые характеристики. 23

2.Корреляционная функция случайных функций, ее свойства. Взаимная корреляционная функция. 24

3. Задача 8.4 25

Экзаменационный Билет №15 25

1.Распределение Пуассона, его числовые характеристики. 25

2. Характеристики случайных функций: 25

3.Задача 8.6. 26

Экзаменационный Билет №16 26

1.Равномерное распределение, его характеристики. 26

2.Понятие случайной функции. Закон распределения случайной функции, плотность распределения случайной функции. 26

3. Задача 8.9. 27

Экзаменационный Билет №17 27

1.Показательное ( экспоненциальное ) распределение, его числовые характеристики. 27

2. Теоремы о числовых характеристиках: , , , . 27

3.Задача 7.3. 29

Экзаменационный Билет №18 29

1. Нормальное распределение случайных величин, его характеристики. 29

2.Теоремы о числовых характеристиках: 29

Задача 7.8. 30

Экзаменационный Билет №19 30

1.Интеграл вероятности, его применение для вычисления вероятности попадания на заданный интервал. 30

2 Числовые характеристики функции случайных величин. 31

3. Задача 18.2. 32

Экзаменационный Билет №20 32

1.Правило 3-х сигм. 32

2. Числовые характеристики системы 2-х случайных величин. 32

3.Задача 6.7. 34

Экзаменационный Билет №21 34

1. Системы случайных величин. Закон распределения, функция распределения. 34

2 .Зависимые и независимые случайные величины . 34

Задача 5.10. 34

Экзаменационный Билет №22 35

1.Плотность распределения системы 2-х случайных величин, плотность распределения отдельных величин, входящих в систему. 35

2.Неравенство Чебышева. 35

3. Задача 21.3 37

Экзаменационный Билет №23 37

1. Условные законы распределения для системы случайных величин. 37

2. Центральная предельная теорема для суммы одинаково распределенных случайных величин. 38

3. Задача 29.7 38

Экзаменационный Билет №24 38

1.Линейные преобразования случайных функций. 38

2.Первое обобщение схемы независимых испытаний. 39

3. Задача 32.9 39

Экзаменационный Билет №25 39

1.О замечательных свойствах законов Пуассона, показательного и нормального з.р.в. 39

2.Первое и второе обобщение схемы независимых испытаний. 39

3. Задача 7.14 40

Экзаменационный Билет №26 40

1.Нормальная функция распределения вероятности. Интеграл вероятности. 40

2.Применение центральной предельной теоремы. 41

3. Задача 15.7 41

Экзаменационный Билет №27 41

1.Закон Пуассона. 41

2.О парной и групповой зависимости случайных событий. 42

3. задача 31.10 42

Экзаменационный Билет №28 42

1.Числовые характеристики случайных функций. 42

2.Линейные преобразования случайных функций. 43

3. Задача 32.11 44

Экзаменационный Билет №29 44

1.Теорема умножения вероятностей. 44

2.Интегральное преобразование случайных функций. 44

3. Задача 3.16 45

Экзаменационный Билет №30 45

1.Теорема сложения вероятностей. 45

2.Дифференциальное преобразование случайных функций. 45

3. Задача 4.16 46

47

Экзаменационный Билет №31 47

1. Случайная величина. Функция и плотность распределения вероятностей для случайных величин. 47

2. Система случайных величин. Функция и плотность распределения вероятностей для системы случайных величин. 48

Задача 11.10 49

Экзаменационный Билет №32 49

1. Случайная величина. Функция и плотность распределения вероятностей для случайных величин. 49

2. Поглощающие цепи Маркова. 50

Задача 29.10 50

Экзаменационный Билет №33 51

1. Регулярные цепи Маркова. 51

2. Система случайных величин. Функция и плотность распределения вероятностей для системы случайных величин. 51

Задача 30.7 51

Экзаменационный Билет №34 51

1. Группированный статистический ряд. Выравнивание опытных данных. 51

2. Система случайных величин. Функция и плотность распределения вероятностей для системы случайных величин. 51

Задача 30.1 52

Экзаменационный Билет №35 52

1. Критерий согласия Пирсона. Проверка правдоподобия гипотез. 52

2. Применение центральной предельной теоремы. 52

Задача 18.16 52

Экзаменационный Билет №36 53

1. Оценка числовых характеристик по неполным данным. 53

2. Числовые характеристики системы 2-х случайных величин 53

Задача 18.13 54

Экзаменационный билет №1

1- Основные понятия теории вероятности.

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Событием называется всякий факт, который в результате опыта может произойти или не произойти.

Вероятностью события называется численная мера степени объективной возможности этого события. Вероятность события А обозначается Р(А), Р или р.

Достоверным называется событие U, которое в результате опыта непременно должно произойти. P(U) = 1.

Невозможным называется событие V, которое в результате опыта не может произойти. P(V) = 0.

Вероятность любого события А заключена между нулем и единицей: 0 < Р(А) < 1.

Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них.

Несколько событий в данном опыте называются несовместными, если никакие два из них не могут появиться вместе.

Несколько событий в данном опыте называются равновозможными, если по условиям симметрии опыта нет оснований считать какое-либо из них более возможным, чем любое другое.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными.

Случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются дискретными

2- Центральная предельная теорема. Различные формы центральной предельной теоремы

Центральная предельная теорема для одинаково распределенных слагаемых

Если независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием и дисперсией , то при неограниченном увеличении n закон распределения суммы

неограниченно приближается к нормальному.

И тогда вероятность того, что случайная величина Y попадет в промежуток , выражается формулой

,

где - функция Лапласа;

; .

Следствие Пусть — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и равносильны утверждению ЦПТ.

Для любых вещественных x < y при имеет место сходимость

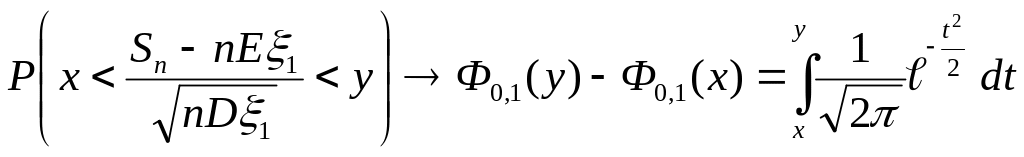
Для любых вещественных x < y при имеет место сходимость

Для любых вещественных x < y при имеет место сходимость

Если — произвольная с. в. со стандартным нормальным распределением, то

Замечание. Еще раз напомним, что функция распределения стандартного нормального закона ищется либо по соответствующей таблице в справочнике, либо с помощью какого-либо программного обеспечения, но никак не путем нахождения первообразной.

Более общей является следующая теорема Ляпунова.

Пусть - независимые случайные величины с математическими ожиданиями и дисперсиями , причем в сумме нет слагаемых, влияние которых на рассеивание суммы подавляюще велико по сравнению с влиянием всех остальных, а также нет большого числа слагаемых, влияние которых на рассеивание суммы исчезающе мало по сравнению с суммарным влиянием остальных, то при закон распределения случайной величины Y неограниченно приближается к нормальному.

3- Задача 30.3 (а).

_{Вероятность выхода из строя не менее 20 конденсаторов:}