5.3.8.4. Расчет по раскрытию трещин, нормальных к продольной оси

При , так как принимаем равным 0, предельная ширина раскры­тия трещин непродолжительная , табл.2 [1], продолжительная .

Изгибающие моменты от нормативных нагрузок, постоянной и длительной 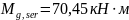, суммарной .

Приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок по формуле (147) [1]:

.

Здесь принимается - плечо внутренней пары сил; , так как усилие обжатия P приложено в центре тяжести площади нижней напрягаемой арматуры; - момент сопротивления сечения по растянутой арматуре.

Приращение напряжений в арматуре от действия полной нагрузки:

.

Ширина раскрытия трещин, нормальных к продольной оси элемента, определяется по формуле(144)[1]:

,

где - коэффициент, принимаемый равным 1 для изгибаемых элементов; φ1-коэффициент, учитывающий длительность действия нагрузки, при учете крат­ковременных нагрузок и непродолжительного действия постоянных и длитель­ных нагрузок ; - коэффициент, принимаемый равным 1,0 при стерж­невой арматуре периодического профиля; - диаметр продольной ар­матуры;

.

Ширина раскрытия трещин от непродолжительного действия всей нагрузки:

.

Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузки:

.

- ширина раскрытия трещин от постоянной и длительной нагрузки;

.

.

Ширина раскрытия трещин:

5.3.8.5. Расчет по деформациям

Прогиб определяем от нормативного значения постоянной и длительной нагрузки. Предельный прогиб .

Вычисляем параметры, необходимые для определения прогиба плиты с учетом трещин в растянутой зоне. Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузки ; суммарная продольная сила равна усилию предварительного обжатия с учетом всех потерь и при ; ; эксцентриситет:

.

Коэффициент при длительном действии нагрузки, определяется по табл.36 [1].

Коэффициент , определяется по формуле 168 [1]:

.

Коэффициент, характеризующий неравномерность деформаций растянутой арматуры на участке между трещинами, находим по формуле 167 [1].

Вычислим кривизну оси при изгибе:

Здесь п. 4.27 [1]; по табл.35 [1] при длительном действии нагрузки; при и допущенном .

Вычислим прогиб:

Условие выполняется.

6.Проектирование ригелей

Для уменьшения конструктивной высоты перекрытия и расхода материала, а также для повышения жесткости каркаса здания ригели рекомендуется проектировать неразрезными прямоугольного сечения или таврового полками вверху или внизу.

Чтобы сборные ригели были неразрезными , надо закладные и накладные детали сопрягаемых элементов сварить и затем омонолитить стыки. Для ригелей следует применять:

- бетон класса В15…В25 (в некоторых случаях В30…В40);

- сталь классов А- II, А- III для продольной рабочей арматуры;

- сталь классов А- I, А- II, А- III, Вр- 1, В- 1 для поперечной и монтажной арматуры.

6.1. Статический расчет

При расчете неразрезные сборные ригели рассматривают (с определенной степенью допущения) как многопролетные неразрезные балки с шарнирным опиранием на наружные стены.

Расчетный размер средних пролетов l_о ригелей принимают равным расстоянию между осями колонн l , а расчетный пролет l_о крайних ригелей – расстоянию от оси опоры его на стене до оси колонны по формуле

l_о = l -0,2+0,3/2, где l – расстояние между разбивочными осями ; 0,3м – величина заделки ригеля в стену; 0,2м – привязка внутренней грани наружной стены к разбивочной оси.

Статически неопределимые железобетонные балки с целью экономии арматурной стали рассматривают с учетом перераспределения усилий.

Ординаты эпюр изгибающих моментов и поперечных сил в неразрезных балках при упругой работе материала определяют по формулам:

- для равномерно распределенной нагрузки М=(α·q+β·v) ·l ² ,

Q=(g·q+d·v) ·l ;

- для сосредоточенных нагрузок М=(a·G+b·V) · l , Q =g·G+d·V,

где a,b,g,d-табличные коэффициенты, определяемые по [10] или [13].

Нагрузку на ригель от пустотных панелей следует принимать равномерно распределенной, а от ребристых сосредоточенной. В этом случае собственный вес ригеля приводиться также к сосредоточенным силам.

Если число сосредоточенных сил в пролете более четырех, то их можно приводить к эквивалентной равномерно распределенной нагрузке.

В промышленных зданиях на ригели таврового сечения с полками внизу укладываются ребристые панели с торцевыми ребрами высотой равной высоте продольного ребра. Поэтому нагрузка от плит принимается равномерно распределенной.

При четырех и более пролетах ригель рассматривают как трехпролетный (все средние пролеты , начиная со второго ,проектируются по среднему пролету трехпролетного ригеля).

Изгибающие моменты и поперечные силы в сечениях ригеля определяют отдельно от действия постоянной и различных комбинаций временной нагрузки. Вычисление ординат эпюр изгибающих моментов и поперечных сил производят в табличной форме (см.п.6.4.3).

По вычисленным ординатам в сечениях на опорах и в середине пролетов необходимо построить эпюры изгибающих моментов и поперечных сил для различных сочетаний постоянной и временной нагрузок (см.п.6.4.3).

Эпюры изгибающих моментов строят по пяти точкам (рис.4). М_о –максимальный изгибающий момент в пролете балки с шарнирным опиранием по концам.

В крайних пролетах максимальный изгибающий момент в пролете будет в сечении, расположенном на расстоянии а=0,425l от свободной опоры.

С учетом пластических деформаций необходимо произвести перераспределение изгибающих моментов ,полученных из расчета упругой схемы ,отдельно для каждого случая суммарного воздействия на балку расчетных временной и постоянной нагрузки. Для перераспределения изгибающих моментов прибавляют треугольные эпюры с произвольными по величине к знаку надопорными ординатами. Ординаты выровненной эпюры моментов в расчетных сечениях во избежание чрезмерного раскрытия трещин в первых пластических шарнирах не должны отличаться более чем на 30% по сравнению с расчетом на упругость.

0,25 l 0,25 l 0,25 l 0,25 l

Рис.4. Эпюра изгибающих моментов ригеля

Построенные для различных загружений участка эпюры моментов с наибольшими ординатами образуют огибающую эпюру моментов.

Принятые при компоновке перекрытия размеры поперечного сечения ригеля уточняют из условия: x= 0,35 (ограничивается армирование сечений ригеля, в которых намечено образование пластических шарниров) по формуле: h₀ = .

Изгибающий момент на грани колонн вычисляют по формуле:

М_гр =М-Q(h/2),

где h-высота сечения колонны в направлении пролета ригеля; Q - поперечная сила на опоре (слева или справа от нее), принимается большее ее значение.

Сечение продольной рабочей арматуры ригеля подбирают по изгибающим моментам в четырех нормальных сечениях: в первом и среднем пролетах, у первой промежуточной опоры и на средней опоре.

Рассчитывают поперечную арматуру в трех наклонных сечениях: у первой промежуточной опоры слева и справа и у крайней опоры.