В данном случае имеем:

Передаточное отношение в первых скобках отрицательно, т.к. колеса 1 и 2 имеют внешнее зацепление, а у колес 2^’ и 3 – зацепление внутреннее. Разделим числитель и знаменатель в формуле Виллиса на ω_H:

Так как ω₃=0 , то получим:

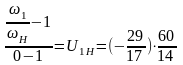
Отсюда окончательно найдем:

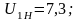
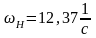
Передаточное отношение второго механизма:

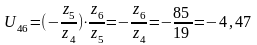
Это отношение отрицательно, так как 4 и 5 колеса имеют внешнее зацеп­ление. Находим передаточное отношение всего механизма:

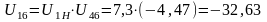
Отрицательная величина передаточного отношения говорит о том, что колеса 1 и 6 вращаются в разные стороны.

Графическое исследование механизма

На листе №4 курсового проекта изображаем схему механизма в масшта­бе. Для этого сначала находим диаметры зубчатых колес по формуле:

d=mz,

принимая условно модуль колес m = 2,5 мм, получим следующие значения диа­метров колес:

d₁=42,5 мм, d₂=72,5 мм,d_2’=35 мм,d₃ = 150мм, d₄ = 47,5 мм, d₅=82,5мм, d₆=212,5 мм.

Принимаем масштаб М 2,5:1, что соответствует масштабному коэффициенту m=2,5 мм, т.е. механизм изображается в увеличенном виде. Обозначаем оси: неподвижное колесоО₃, подвижные колеса: О_1, О₄, О₅, О₆, колесо вращающееся в пространстве (подвижная ось сателлита) О₂. Места зацепления зубчатых колес отмечаем буквами А, В, С,D( права от схемы механизма проводим вертикальную линию у, на которую сно­сим все точки неподвижных осей, обозначая их строчными буквами о₁ ,о₂ , о₃ , о₄,о₅, о₆ . На горизонтальной линии, проходящей через точку А, от вертикали у откладываем в ту или иную сторону произвольный отрезок fa, изображающий скорость точки А. Затем соединяем точки а и о₁ , получая линию распределения скоростей колеса I. Точка В неподвижна, и она также сносится на линию у и обозначается В. Соединяем точку В и А, получая отрезок распределения скорости вращения колес 2 и 2^’. На линии распределения скоростей колеса 2 отмечаем точку О₂. Соединяем точку О₂ и О₃. Продолжаем этот отрезок до пересечения с линией распределения зацепления колес 4 и 5 (точка С). Соединяем точку С с О₅ (линия распределения скоростей колеса 5). Продлеваем этот отрезок до линии зацепления колес 5 и 6 (точка D). Соединяем точку D с О₆ , получаю линию распределения скоростей колеса 6.

Изображаем произвольную горизонтальную прямую х. Ниже этой прямой также произвольно отмечаем точку о, из которой проводим одну вертикальную линию и два луча, параллельные прямым распределения скоростей колес 1 и 6. Получаем точки k, q,p. Замеряем расстояния qp и qk и находим их отношение:

Отрезки qp и qk располагаются от вертикали с разных сторон, значит передаточное отношение получается отрицательным.

Угловая скорость колеса 6:

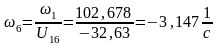
Сравнивая результаты, полученные аналитическим и графическим мето­дами, отмечаем высокую точность вычислений и построений.

Заключение

Ознакомились с основными методами кинематического и силового анализа рычажных механизмов, а также с элементами проектирования кинематических схем механизмов. Исследовали кулачковые и зубчатые механизмы графическим и аналитическим методами.

Научились самостоятельно применять теоретические положения ТММ при исследовании и проектировании конкретного механизма, что способствовало усвоению и закреплению теоретического материала, излагаемого на лекциях и в учебниках.

Кроме того, проведение курсового проектирования по ТММ привило некоторые навыки научно-исследовательской работы.