4 Синтез кулачкового механизма
Построение графика перемещений толкателя
Известны
следующие параметры: безмасштабный
график скорости толкателя, ход
(максимальное перемещение) толкателя
φ=60º – для кулачкового механизма с
качающимся толкателем, угловая скорость
кулачка
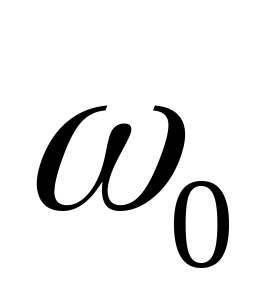=100
1/с.
Требуется построить график перемещений толкателя.
Изображаем график скорости толкателя таким образом, чтобы горизонтальная ось N (t) ,обозначающая номера положений механизма, имела длину L=240 мм (в нашем случае L=120 мм), а максимальные ординаты равны
h1=80 мм; h2=162 мм. Для правильного построения графика перемещений необходимо, чтобы суммарная площадь фигур, расположенных над осью N, была бы равна площади фигур, расположенных под осью N. В рассматриваемом случае площадь 1-ого треугольника равняется площади 2-ого. Находим площади этих фигур по известным формулам и приравниваем их:
Для графика перемещений выбираем максимальную ординату φ', например, φ'=100 мм. Масштабный коэффициент площади будет равен
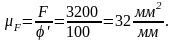
Разбиваем график скоростей на 12 интервалов и определяем площади фигур для каждого интервала, замеряя высоты и основания треугольников и трапеций.
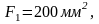
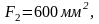
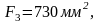
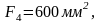
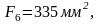
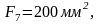
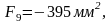
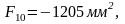
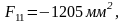
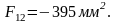
Площади под осью N отрицательны.
Находим ординаты на графике перемещений
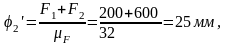
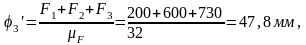
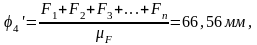
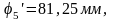
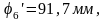
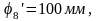
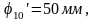
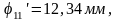
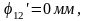
Полученные ординаты откладываем от оси N и через найденные точки проводим плавную кривую, являющуюся графиком перемещений толкателя
Определяем
масштабные коэффициенты
µS,
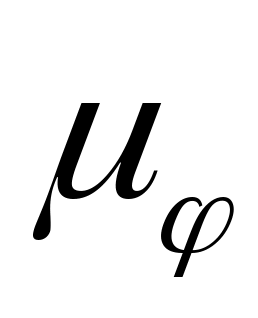
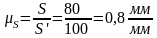
Для
нахождения коэффициента
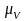воспользуемся формулой
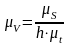
Здесь
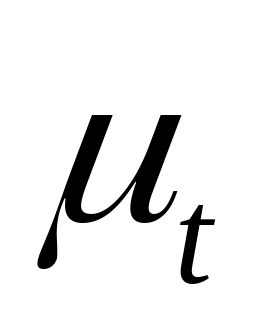– масштабный коэффициент времени,
который определяется из формулы:
.
Величина
находится следующим образом. На графике
перемещений в любой точке m
проводим касательную τ.
Точку m
сносим на ось φ,
получая точку, через которую проводим
луч, параллельный касательной. Луч
пересекает ось N
в точке p.
Расстояние от точки p
до начала координат и есть величина
h = 40 мм
Для нашего случая получаем
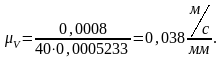
Изображаем график ускорения толкателя таким образом, чтобы горизонтальная ось N (или t), обозначающая номера положений механизма (или время), имела длину L=120. Для правильного построения графика необходимо проанализировать график изменения скорости толкателя. В рассматриваемом случае скорость на участке 0-2 растет, для получения ускорения воспользуемся формулой:
Где:
Так
как Т период разбили на 12 частей, то
а
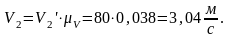
На участке от 2-8 скорость снижается:
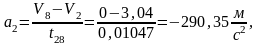
Где:
Так
как Т период разбили на 12 частей, то:
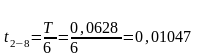
а V8=0;
На участке 8-10 скорость падает.
Где: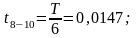
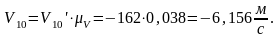
На участке 10-12 скорость возрастает.
Где:
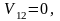
По оси ординат откладываем для a1’=20 мм, тогда масштабный коэффициент графика ускорений равен:
Тогда
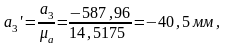
Синтез кулачкового механизма с качающимся толкателем
Известны
следующие параметры механизма: график
перемещений толкателя, минимальный
радиус кулачка
,
радиус ролика
ход толкателя
,
межосевое расстояние
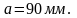скорость
кулачка
1/с, направление вращения кулачка – по
часовой стрелки.
Требуется построить профиль кулачка.
Выбираем масштабный коэффициент кулачкового механизма
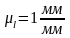
Находим
размеры на чертеже:
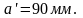
Из
произвольной точки О проводим окружность
радиуса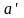
,
которую делим на 12 частей, получая точки
,
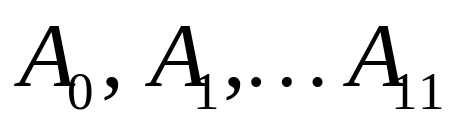причем нумерацию этих точек ведем в
направлении, обратном направлению
вращения кулачка. Все эти точки соединяем
с точкой O.
Вычисляем значения углов
по
формуле:
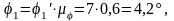
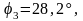
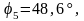
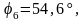
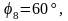
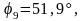
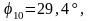
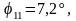
Из
точкиO
делаем засечку радиусом
,
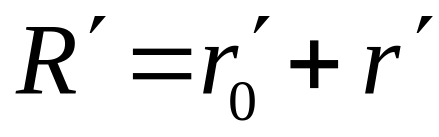а из точки
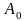- засечку радиусом
получая
.
Замеряем угол
.
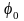Из точки
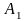проводим луч под углом
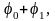на котором откладываем величину
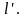Получаем точку
и т. д. Из точки
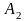проводим луч под углом
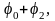на котором откладываем величину
Получаем точку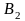
и т. д. Точки
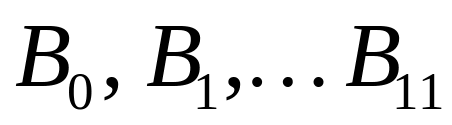соединяем плавной кривой, получая
центровой (теоретический) профиль
кулачка.
Для оценки точности построений найдем величину скорости толкателя в одном из положений, например, в третьем. Замеряем длину ординаты, которая в данном случае равна ω3 = h1 =80 мм . Следовательно:
ω3 = ω3’* µω = 80*0,038=3,04 1/c
Построим план скоростей механизма для того же положения, используя векторное уравнение:
VB3’=VB3+VB3’B3
где: VB3 - скорость точки В3, принадлежащей кулачку,
VB3’ - скорость точки, принадлежащей толкателю.
Скорость точки B3 определяем по формуле:
VB3 = ω0*ρ3;
где ρ3 - действительная величина радиуса центрового профиля кулачка.
Её можно найти через коэффициент, учитывая, что на чертеже ρ3= ОВ3. Следовательно ρ3= ρ3’*µl = 73*1,2=87,6 мм (0,0876м).
Тогда VB3 = 100*0,0876=8,76;
Выбираем масштабный коэффициент для плана скоростей, изображая вектор VB3 отрезком pb3= 60 мм.
Из полюса р проводим вектор перпендикулярно OB3, в сторону вращения кулачка. В точке B3 центрового профиля проводим касательную τ, которую переносим в точку b3 на плане скоростей.
Из полюса p проводим линию, перпендикулярную толкателю А3B3. Получим векторы VB3’ и VB3’B3 . Замеряем длину вектора и вычисляем его:
VB3’= pb3*µV = 18*0,146 = 2,628 м/с.
Определяем угловую скорость толкателя
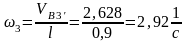
Таким образом, скорости толкателя, полученные двумя способами, отличаются друг от друга на 3,9 % , что свидетельствует о правильности построений.
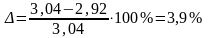
5 Кинематическое исследование зубчатого механизма с одинарным сателлитом
Аналитическое исследование механизма
Даны числа зубьев колес зубчатого механизма с одинарным сателлитом: z1 =17, z2 = 29, z3=60, z4=19, z5=33. Известночисло оборотов входного колеса n1 = 981. Требуется определить передаточное отношение U16 и угловую скорость ω6 .
Разбиваем механизм на две составляющие. Первый механизм, состоящий из колес 1,2,3 – планетарный, имеющий колеса 1,2,3 и водила h. У этого механизма ось колеса 2 движется в пространстве. Второй механизм, состоящий из колес 4,5,6, является простым механизмом с неподвижными осями.
Находим недостающие значения чисел зубьев колес 2’ и 6:
для колеса 2’: z1+z2 = z3-z2’;
z2’= z3-z1-z2 = 60-17-29 = 14;
для колеса 6: z6 = z4+2z5;
z6 = 19+2*33 = 85.
Угловая скорость колеса 1:
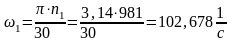
Находим передаточное отношение всего механизма:
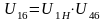
где
–
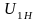передаточное отношение первого механизма;
–
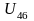передаточное отношение второго механизма.
Передаточное отношение UlH планетарного механизма определяем, используя формулу Виллиса:
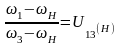
Здесь ω1 - угловая скорость входного центрального колеса 1,
ωH - угловая скорость водила h,
U13(H) - передаточное отношение от колеса 1 к водилу h при остановленном водиле h.