
- •Содержание
- •Введение
- •1 Кинематический анализ рычажного механизма (120º) кривошипно-кулисный механизм
- •2 Кинематический анализ рычажного механизма (300º) кривошипно-кулисный механизм
- •3 Силовой анализ рычажного механизма (120º) кривошипно-кулисный механизм
- •4 Синтез кулачкового механизма
- •В данном случае имеем:
- •Передаточное отношение второго механизма:
- •Заключение
- •Список использованных источников
3 Силовой анализ рычажного механизма (120º) кривошипно-кулисный механизм
Известны следующие параметры механизма:
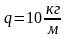 ,
,
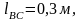
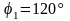 ,
,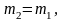
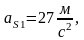
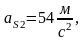
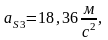
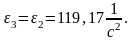
Требуется определить реакции в кинематических парах и уравновешивающую силу.
Изображаем
механизм в заданном положении с
обозначением масштабного коэффициента
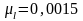 м/мм.
На механизм действуют следующие силы.
м/мм.
На механизм действуют следующие силы.
1.Сила
полезного сопротивления
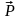 ,
указываемая в задании. Она приложена в
точке С кулисы 3 и направлена перпендикулярно
ей.
,
указываемая в задании. Она приложена в
точке С кулисы 3 и направлена перпендикулярно
ей.
2.Силы
тяжести
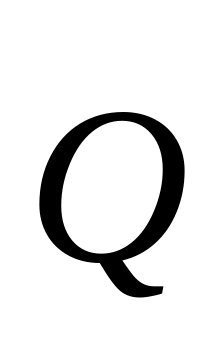 ,
определяемые через массы звеньев,
которые можно условно найти по формуле
,
определяемые через массы звеньев,
которые можно условно найти по формуле
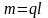 ,
где q–масса
единицы длины звена, l
–длина звена:
,
где q–масса
единицы длины звена, l
–длина звена:
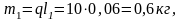
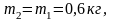
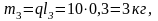
Следовательно,
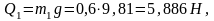
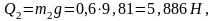
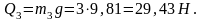
Силы тяжести прикладываются в центрах масс S1, S2, S3 и направлены вертикально вниз.
3.Силы
инерции звеньев
 ,
определяемые по формуле
,
определяемые по формуле
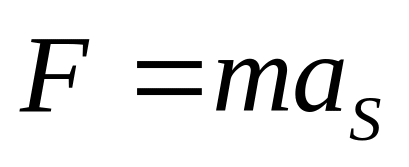
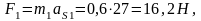
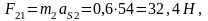

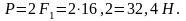
Эти
силы прикладываются в центрах масс и
направлены они в стороны, обратные
ускорениям
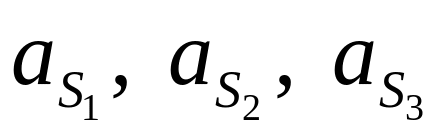 .
.
4.Момнеты
сил инерции М,
которые можно найти по формуле
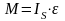 ,
где IS
–моменты инерции звеньев относительно
центральных осей:
,
где IS
–моменты инерции звеньев относительно
центральных осей:
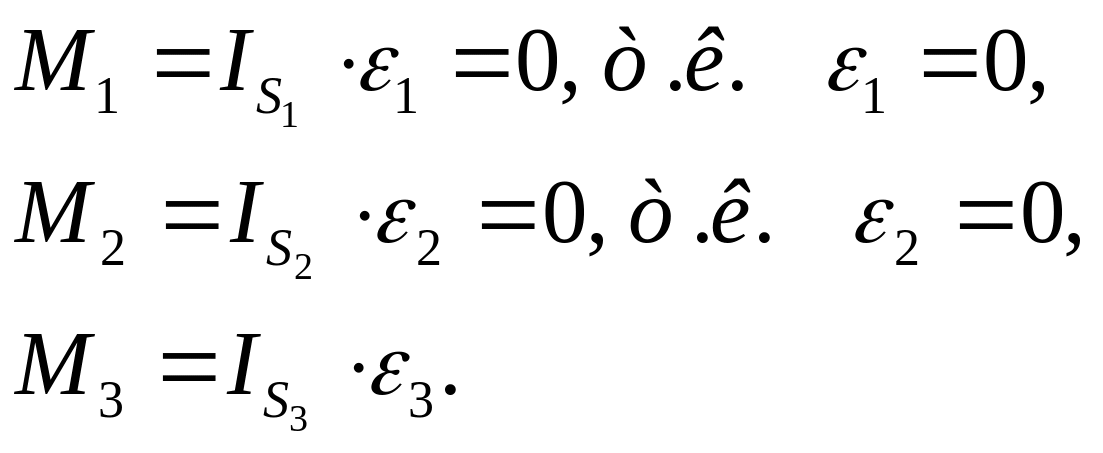
т.к. ε1 = 0; ε2 = 0
Моменты
инерции звеньев определяем по формуле
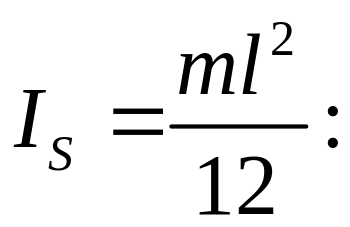
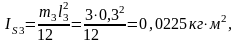
Следовательно,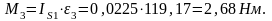
Моменты сил инерции М направлены в стороны, обратные угловым ускорениям.
5.Уравновешивающая
сила
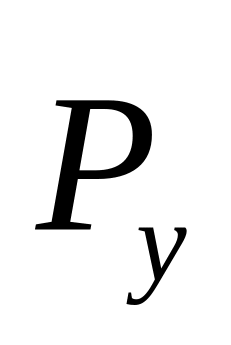 ,
прикладываемая в точке А кривошипа 1 и
направлена перпендикулярно ему.
,
прикладываемая в точке А кривошипа 1 и
направлена перпендикулярно ему.
Находим
длины плеч, замеряя их на чертеже и
умножая на
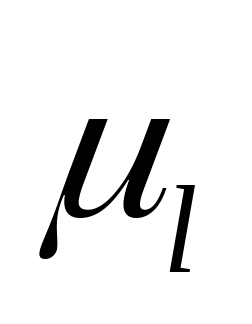 :
:



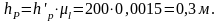
Записываем уравнение моментов относительно точки В:
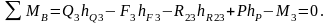
Отсюда


Так как эта реакция оказалась положительной, то её оставляем в таком же положении.
Для
нахождения реакции
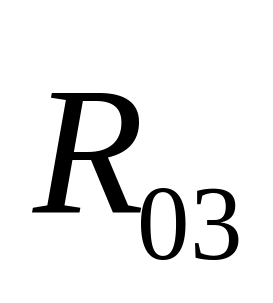 составляем силовой многоугольник в
масштабе
составляем силовой многоугольник в
масштабе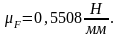 Вычисляем длины векторов сил:
Вычисляем длины векторов сил:
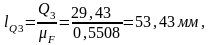
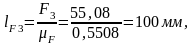
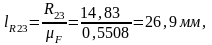

Векторы
в многоугольнике идут в любом порядке.
Например, начинаем с силы
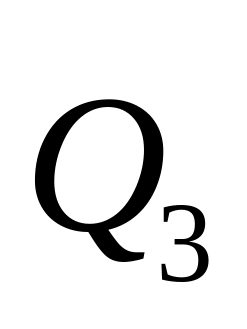 и заканчиваем вектором
и заканчиваем вектором
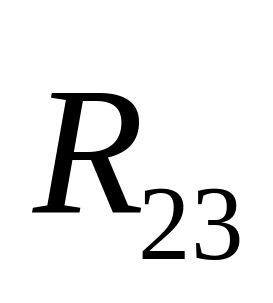 .
Замыкающий вектор
имеет направление
в исходную точку. Замеряем длину силы
и умножаем на масштабный коэффициент
.
Замыкающий вектор
имеет направление
в исходную точку. Замеряем длину силы
и умножаем на масштабный коэффициент
 :
:

Вектор в шарнире В перечеркиваем и направляем его так, как он идет в силовом многоугольнике.
Изображаем
отдельно камень 2, на который действует
сила
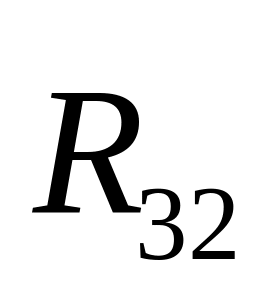 ,
равная силе
и противоположно направленна, т.е.
,
равная силе
и противоположно направленна, т.е.
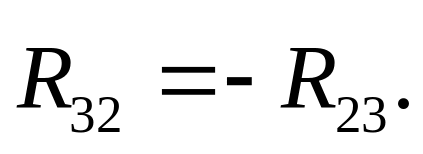 Выбираем
Выбираем
 и строим силовой многоугольник.
и строим силовой многоугольник.



Замыкающий
вектор в нем представляет реакцию
 ,
который направлен в начало первой силы
,
который направлен в начало первой силы Вычисляем его значение:
Вычисляем его значение:
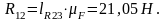
Вектор
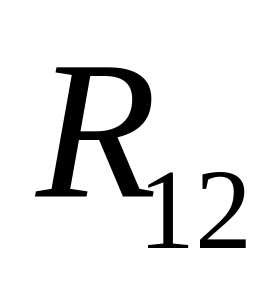 перечеркиваем и направляем так, как он
идет в силовом многоугольники.
перечеркиваем и направляем так, как он
идет в силовом многоугольники.
Изображаем
отдельно кривошип 1 со всеми силами,
причем реакцию
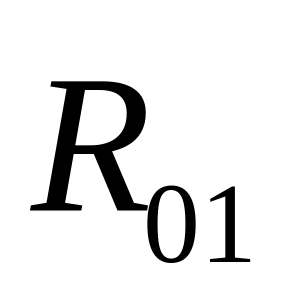 направляем пока произвольно, а сила
направляем пока произвольно, а сила
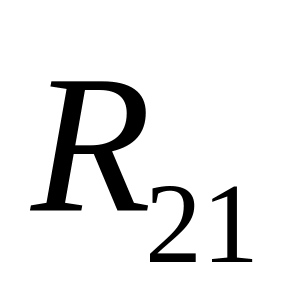 такая же как и
такая же как и
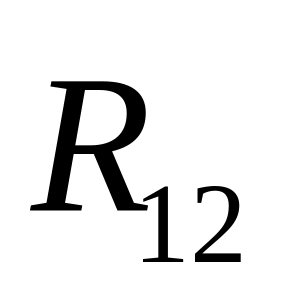 ,
но направлена в другую сторону, т.е.
,
но направлена в другую сторону, т.е.
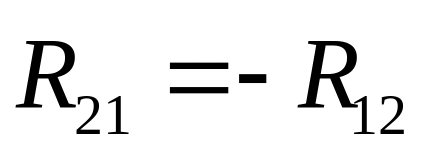 .
Из точки О к силам проводим перпендикуляры,
замеряем их и находим истинную длину:
.
Из точки О к силам проводим перпендикуляры,
замеряем их и находим истинную длину:
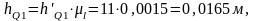
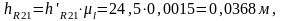
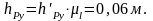
Из
уравнения моментов относительно точки
О находим
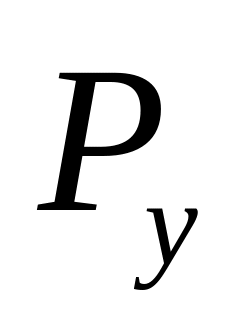 :
:

Отсюда
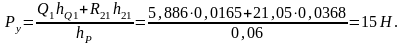

Так как эта реакция оказалась положительной, то её оставляем в этом же положении.
Строим
силовой многоугольник для кривошипа в
масштабе
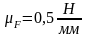 ,
из которого находим
,
из которого находим
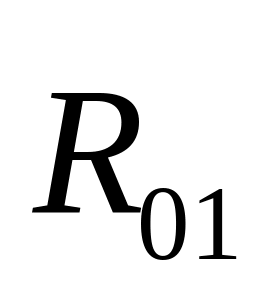 ,
идущий в начало силы
,
идущий в начало силы
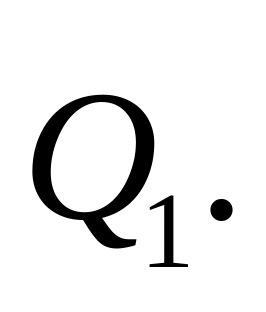
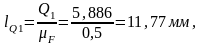


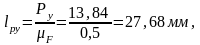
Замеряем длину вектора и находим реакцию в шарнире О:
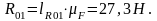
Вектор перечеркиваем и направляем так, как он идет в силовом многоугольнике.
Для
проверки точности расчетов и построений
найдем уравновешивающую силу по методу
Жуковского. Момент силы инерции
 звена 3 заменяем парой сил
звена 3 заменяем парой сил
 и
и
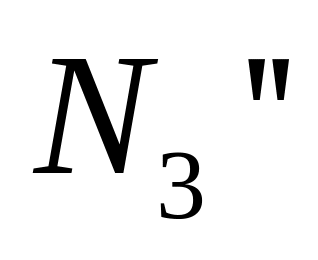 ,
действующих, например, в точках В и С и
направленных перпендикулярно кулисе.
При этом направление пары сил должно
совпадать с направлением момента
.
Найдем величины этих сил:
,
действующих, например, в точках В и С и
направленных перпендикулярно кулисе.
При этом направление пары сил должно
совпадать с направлением момента
.
Найдем величины этих сил:
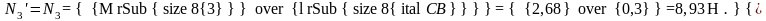
Переносим с первого листа курсовой работы план скоростей, на который помещаем все внешние силы повернув на 900 , приложив их в соответствующие точки. Из полюса скоростей р проводим к силам перпендикуляры, замеряем их длины
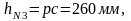
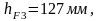

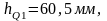
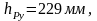

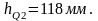
Далее записываем уравнение моментов:
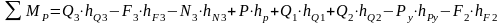
Отсюда находим:
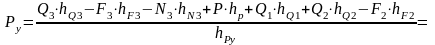
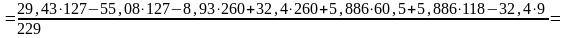
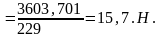
Сравнение результатов, полученных двумя способами, говорит о том, что погрешность вычислений и построений находится в пределах нормы.

