2 Кинематический анализ рычажного механизма (300º) кривошипно-кулисный механизм

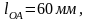
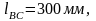
Известны следующие параметры механизма: 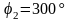, . Направление вращения кривошипа – по часовой стрелки.

Требуется определить линейные скорости и ускорения точек механизма, а также угловые скорости и ускорения звеньев.

Построение плана положений механизма

Выражаем все длины звеньев в метрах:

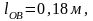
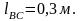
Определяем масштабный коэффициент длин, представляющий собой отношение действительной длины в метрах к длине отрезка на чертеже в миллиметрах. Изображаем длину кривошипа l_BC на чертеже отрезком l_BC^’, равным, например, 80 мм. Тогда масштабный коэффициент будет иметь величину

Остальные длины звеньев, изображенные на чертеже, будут иметь следующие значения:

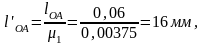
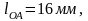Из произвольной точки O под углом откладываем отрезок получаем точку А, которую соединяем с точкой В, отстоящую от точки О на расстояние 48 мм. Через точки А и В проводим прямую на которой откладываем отрезок 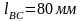тем самым получаем точку С. Прямоугольником изображаем камень.

Построение плана скоростей

Определяем скорость точки А, принадлежащей кривошипу 1 и камню 2:

Находим масштабный коэффициент скоростей, для чего полученную величину делим на длину вектора этой скорости, выбранную равной pa=40мм:

Из произвольной точки p (полюса скоростей) проводим вектор , который перпендикулярен кривошипу и направлен в сторону его вращения. Длина этого вектора равна 40 мм. Скорость точки A’, принадлежащей кулисе 3, находим графически, используя векторные уравнения

Так как скорость точек О и В равны нулю, то точки и помещаем в полюсе. Система уравнений решается следующим образом. Из точки проводим прямую, параллельную кулисе, а из полюса перпендикулярную к ней. На пересечении получаем точку a^’. Ставим две стрелки, получая скорости и Для нахождения точки на плане скоростей воспользуемся выражением

Замеряем на рисунке и , находим :

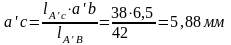
Точку c соединяем с полюсом, получая скорость . Численное значения полученных скоростей находим через коэффициент , замеряя длины векторов:

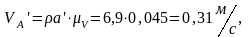
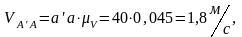
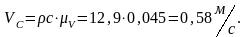
Вычисляем угловую скорость кулисы и камня:

_{Здесь величина} определяется умножением замеренной величины на масштабный коэффициент

.

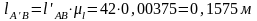Следовательно,

.

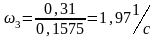Построение плана ускорений

Определяем ускорение точки А.

Так как , то

Тогда

.

_{Масштабный коэффициент можно найти путем деления ускорения точки А на длину вектора на чертеже, выбранную равной} πa = 75 мм:

.

Ускорение точки А направлено от точки А к центру О параллельно кривошипу.

Из произвольной точки - полюса ускорений проводим вектор длиной 75 мм. Ускорение точки кулисы находим графо-аналитически, решая систему векторных уравнений

Ускорения и , поэтому точки о и b помещаем в полюсе. Определяем по модулю ускорение и :

_,

.

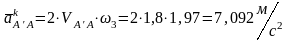_{Находим длины векторов этих ускорений:}

Для определения ускорения Кориолиса нужно вектор повернуть по направлению на . Следовательно, будет направлен вверх перпендикулярно кулисе. Из точки проводим ускорение , а из полюса – ускорение , которое идет параллельно кулисе BC от точки к точки В. Перпендикулярно к и проводим прямые, которые пересекаются в точки . Эту точку соединяем с полюсом, получая вектора , , .

Точку на плане ускорений определяем, решая равенство

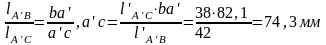
Обозначаем вектор стрелкой.

Точки и находятся в серединах отрезков и , а точка совпадает с точкой . Соединяя точки и с полюсом, получаем векторы и . Замеряем длины всех неизвестных векторов ускорений и через масштабный коэффициент определяем их модули:

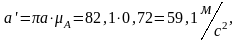
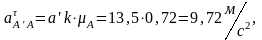
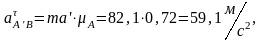
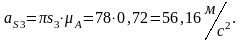
_{Вычисляем угловое ускорение кулисы, которое равно угловому ускорению камня:}

Перенося вектор в точку механизма, находим, что угловое ускорение направлено почасовой стрелки. Отмечаем его дуговой стрелкой.

В таблицу 1 сведены расхождения между аналитическими и графическими значениями.

Таблица 1 – Расхождения между аналитическими и графическими значениями

	Аналитическое значение	Графическое значение	Погрешность, %
	1,85	1,8	2,7
ω3	2,05	1,97	3,9
	9,89	9,72	1,72
ε3	379,82	375,24	1,2