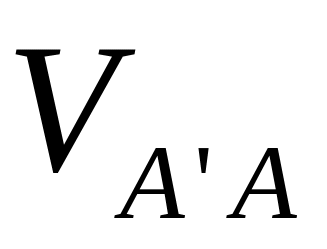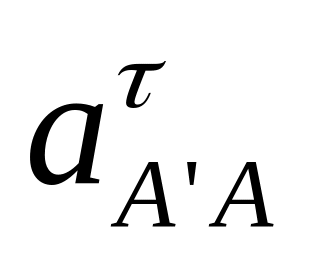МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра Механики
Расчетно-пояснительная записка к курсовому проекту по Теории машин и механизмов Тема: «Синтез и анализ рычажного, кулачкового, зубчатого механизмов»
Выполнил:	Степанов Юрий Сергеевич, студент МТФ гр. 3М-19
Проверил:	Краснер Станислав Юрьевич
Витебск 2012

Содержание

ВВЕДЕНИЕ 3

1 КИНЕМАТИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА (120º) КРИВОШИПНО-КУЛИСНЫЙ МЕХАНИЗМ 4

2 КИНЕМАТИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА (300º) КРИВОШИПНО-КУЛИСНЫЙ МЕХАНИЗМ 11

3 СИЛОВОЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА (120º) КРИВОШИПНО-КУЛИСНЫЙ МЕХАНИЗМ 18

4 СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА 25

5 Кинематическое исследование зубчатого механизма с одинарным сателлитом 32

Аналитическое исследование механизма 32

Даны числа зубьев колес зубчатого механизма с одинарным сателлитом: z₁ =17, z₂ = 29, z₃=60, z₄=19, z₅=33. Известночисло оборотов входного колеса n₁ = 981. Требуется определить передаточное отношение U₁₆ и угловую скорость ω₆ . 32

Разбиваем механизм на две составляющие. Первый механизм, состоящий из колес 1,2,3 – планетарный, имеющий колеса 1,2,3 и водила h. У этого механизма ось колеса 2 движется в пространстве. Второй механизм, состоящий из колес 4,5,6, является простым механизмом с неподвижными осями. 32

Находим передаточное отношение всего механизма: 33

В данном случае имеем: 33

Передаточное отношение второго механизма: 34

ЗАКЛЮЧЕНИЕ 36

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 37

Введение

Курсовое проектирование по теории механизмов и машин имеет следующие цели и задачи:

а) ознакомить студентов с основными методами кинематического и силового анализа, а также синтеза механизмов, используя графические и аналитические методы;

б) научить студентов самостоятельно применять положения курса при исследовании и проектировании конкретных механизмов, что должно способствовать усвоению и закреплению теоретического материала;

в) привить студентам некоторые навыки применения ЭВМ для анализа и синтеза механизмов, а также при проведении научно-исследовательских работ.

1 Кинематический анализ рычажного механизма (120º) кривошипно-кулисный механизм

_{Известны следующие параметры механизма:} l_OA = 60 мм, l_OB = 180 мм,

_{lBC = 300 мм , φ1 = 1200, ω1 = 30 рад/с.}

Направление вращения кривошипа – по часовой стрелки. Требуется определить линейные скорости и ускорения точек механизма, а также угловые скорости и ускорения звеньев.

Построение плана положений механизма

Выражаем все длины звеньев в метрах:

l_OA = 0,06 мм, l_OB = 0,18 мм, l_BC = 0,3 мм.

Определяем масштабный коэффициент длин, представляющий собой отношение действительной длины в метрах к длине отрезка на чертеже в миллиметрах. Изображаем длину кривошипа 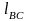на чертеже отрезком 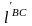, равным, например, 80 мм. Тогда масштабный коэффициент будет иметь величину:

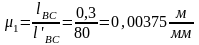
Остальные длины звеньев, изображенные на чертеже, будут иметь следующие значения:

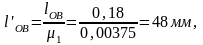
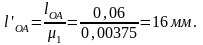
Из произвольной точки O под углом φ₁ = 120⁰ откладываем отрезок

l_OA’ = 16 мм, получаем точку А, которую соединяем с точкой В, отстоящую от точки О на расстояние 48 мм. Через точки А и В проводим прямую на которой откладываем отрезок l_BC’ = 80 мм, тем самым получаем точку С. Прямоугольником изображаем камень.

Построение плана скоростей

Определяем скорость точки А, принадлежащей кривошипу 1 и камню 2:

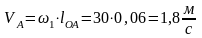
Находим масштабный коэффициент скоростей, для чего полученную величину делим на длину вектора этой скорости, выбранную равной pa=40мм:

Из произвольной точки 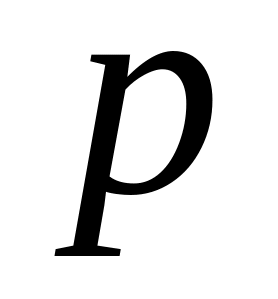(полюса скоростей) проводим вектор 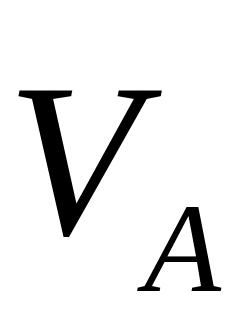, который перпендикулярен кривошипу и направлен в сторону его вращения. Длина этого вектора равна 40 мм. Скорость точки A’, принадлежащей кулисе 3, находим графически, используя векторные уравнения

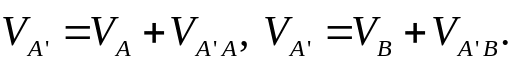
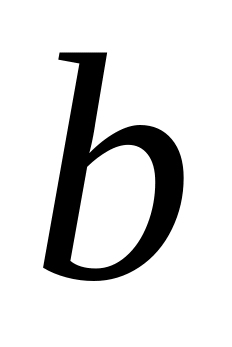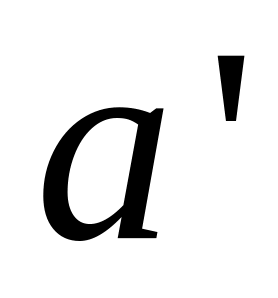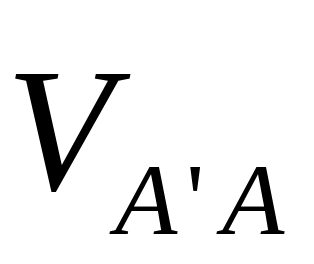Так как скорость точек О и В равны нулю, то точки и помещаем в полюсе. Система уравнений решается следующим образом. Из точки проводим прямую, параллельную кулисе, а из полюса перпендикулярную к ней. На пересечении получаем точку . Ставим две стрелки, получая скорости и 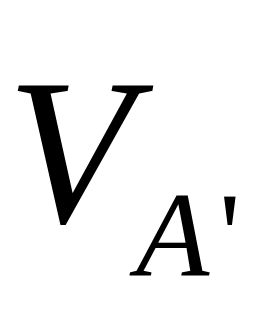Для нахождения точки с на плане скоростей воспользуемся выражением

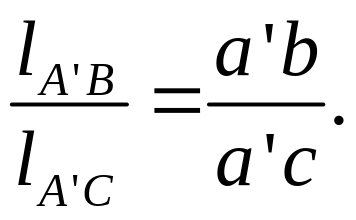
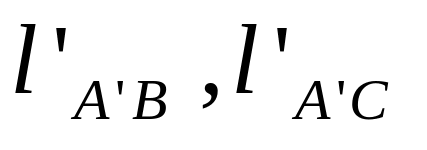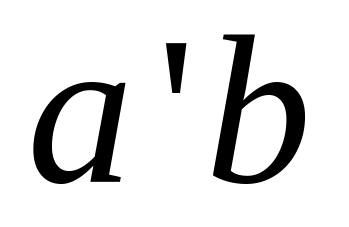Замеряем на рисунке и , находим :

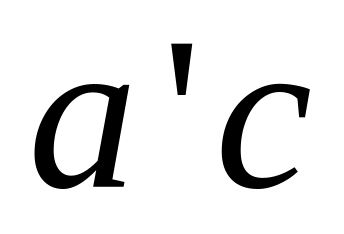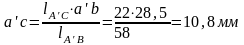
Точку c соединяем с полюсом, получая скорость 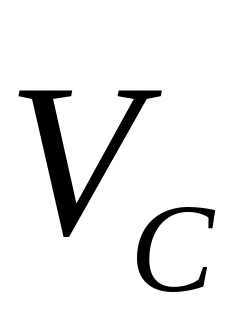. Численное значения полученных скоростей находим через коэффициент 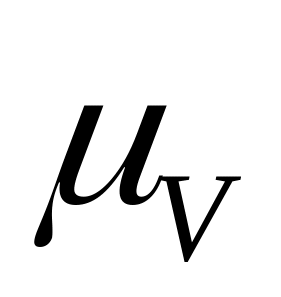, замеряя длины

векторов:

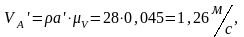
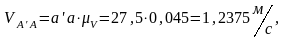
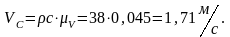
Вычисляем угловую скорость кулисы и камня:

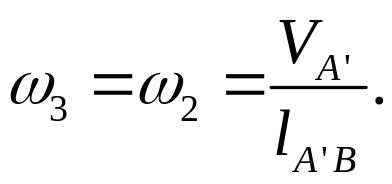
_{Здесь величина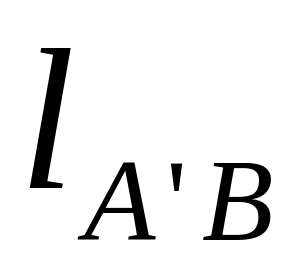} определяется умножением замеренной величины 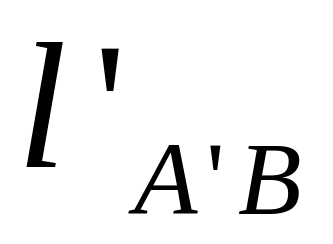на масштабный коэффициент

.

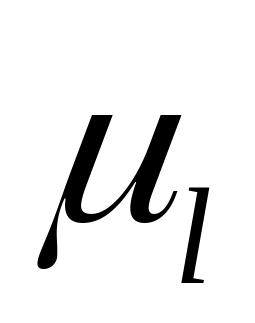
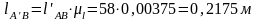Следовательно:

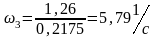
Построение плана ускорений

Определяем ускорение точки А.

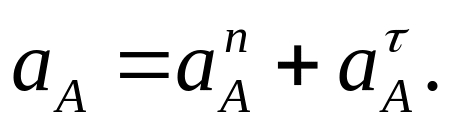
Так как 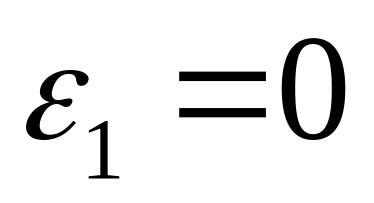, то

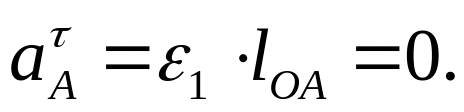
Тогда

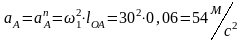
_{Масштабный коэффициент можно найти путем деления ускорения точки А на длину вектора на чертеже, выбранную равной} πa =75 мм:

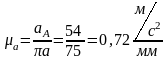
Ускорение точки А направлено от точки А к центру О параллельно кривошипу.

Из произвольной точки π - полюса ускорений проводим вектор длиной 75 мм. Ускорение точки кулисы находим графо-аналитически, решая систему векторных уравнений

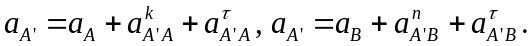
Ускорения 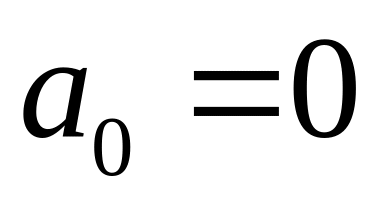и 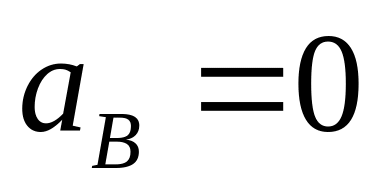, поэтому точки о и b помещаем в полюсе. Определяем по модулю ускорение 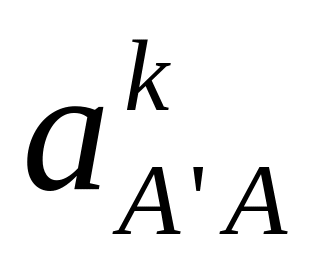и :

_,

.

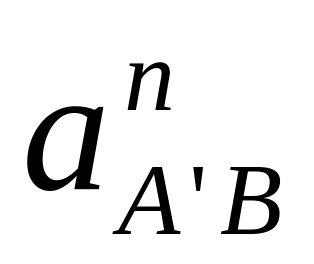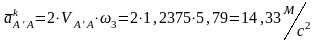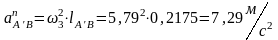_{Находим длины векторов этих ускорений:}

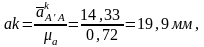
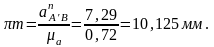
Для определения ускорения Кориолиса нужно вектор повернуть по направлению 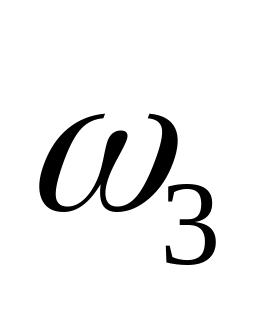на 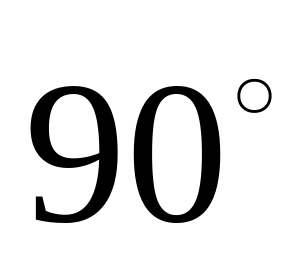. Следовательно, будет направлен вверх перпендикулярно кулисе. Из точки проводим ускорение , а из полюса – ускорение , которое идет параллельно кулисе BC от точки 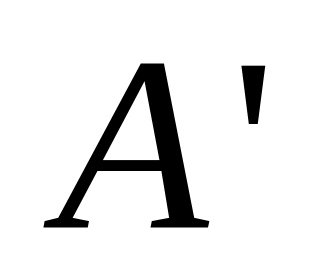к точки В. Перпендикулярно к и проводим прямые, которые пересекаются в точки . Эту точку соединяем с полюсом, получая вектора , , .

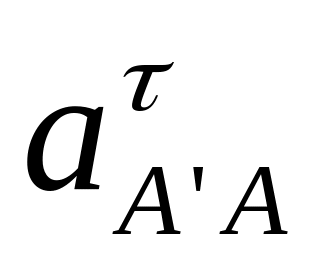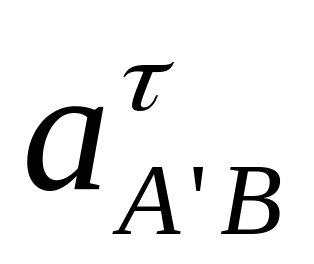Точку на плане ускорений определяем, решая равенство:

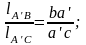
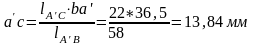
Обозначаем вектор 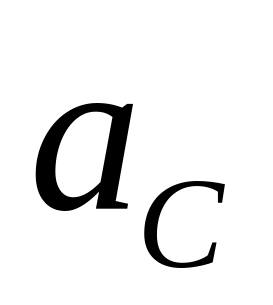стрелкой.

Точк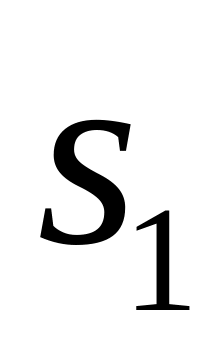и и 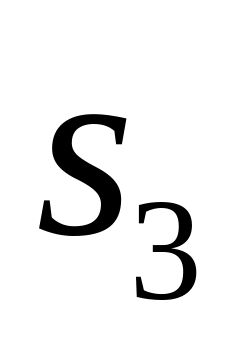находятся в серединах отрезков πa и πc, а точка 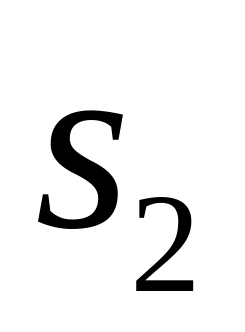совпадает с точкой a. Соединяя точки и с полюсом, получаем векторы и . Замеряем длины всех неизвестных векторов ускорений и через масштабный коэффициент определяем их модули:

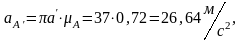
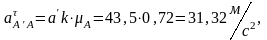
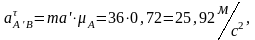
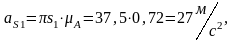
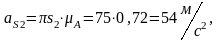
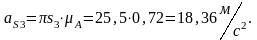
_{Вычисляем угловое ускорение кулисы, которое равно угловому ускорению камня:}

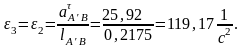
Перенося вектор 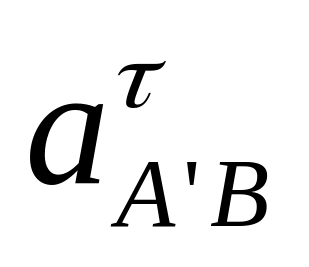в точку A механизма, находим, что угловое ускорение направлено против часовой стрелки. Отмечаем его дуговой стрелкой.

Таблица погрешностей

	Аналитическое значение	Графическое значение	Погрешность, %
	1,28	1,2375	3,3
ω3	5,85	5,79	1
	32,1	31,32	2,4
ε3	121,7	119,17	2,07