П.2.Типы алгоритмов.

Опыт практической алгоритмизации накопленный в связи с составлением программ для ЭВМ привел к формированию особенной методики структурированной организации алгоритмов, использование которой позволяет:

1. уменьшить вероятность ошибок при разработке алгоритмов решения задач;

2. упростить понимание алгоритмов;

3. модифицировать алгоритм без существенной перестройки всей его структуры.

Эту методику называют структурным подходом. При структурном подходе к конструированию алгоритмов, они как бы собираются из 6 основных базовых структур: следование, развилка полная, развилка неполная, цикл - до, цикл - пока, цикл с параметром.

Следование

С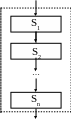 труктура состоит из 2х или более функциональных (арифметических) блоков, изображенных в виде прямоугольников (Рис. 55).

S₁, S₂ и S_n - предписываемые действия.

Словесная запись данной структуры

следующая:

исполнить S₁,S₂,...,S_n

Рис. 55

Развилка

Д

Рис. 56

анная структура организует выполнение одного из 2х указанных действий S1 и S2 в зависимости от выполнения условия P (Рис. 56). Различают полную и неполную развилки.

Словесная запись полной развилки: если P истинно, то исполнить S1, иначе исполнить S2. (или в сокращенной форме: если Р, то S1, иначе S2). Словесная запись неполной развилки: если Р, то S1 (альтернативное действие S2 отсутствует)

Цикл

Данная структура описывает циклические, т.е. многократно повторяющиеся действия. Структура повторения может быть 3 типов:

Цикл – пока (Рис. 57)

З десь P – условие продолжения цикла, S – тело цикла.

Словесная запись структуры цикла-пока: пока Р истинно исполнять S

Выполнение цикла-пока начинается с проверки условия, поэтому этот цикл называют циклом с предусловием. Переход к выполнению тела цикла осуществляется только в том случае, если условие Р выполняется, т.е. истинно, в противном случае, происходит выход из цикла, поэтому данный цикл называют также циклом с предусловием.

Цикл – до (Рис. 58)

Здесь P – условие окончания цикла, S – тело цикла. Словесная запись структуры цикла-до: исполнять S до истинности Р

В ыполнение структуры цикл-до начинается с выполнения действия S. Т.о., тело цикла будет обязательно исполнено хотя бы 1 раз. После этого происходит проверка условия Р, поэтому данный цикл называют также циклом с постусловием. Если условие Р - ложно, то осуществляется переход к повторному выполнению тела цикла S. Когда же условие Р становится истинным, то происходит выход из цикла.

Т.о., условия Р в вариантах цикла-пока и цикла-до противоположны. В цикле-пока Р - условие продолжения цикла, а в цикле-до Р - условие окончания цикла.

Цикл с параметром (Рис. 59)

О днако в теории циклических алгоритмов существует еще одна форма записи управляющей структуры цикл - цикл с параметром (или цикл со счетчиком).

Здесь I – параметр цикла, S – тело цикла. Параметр I изменяется от А до В с шагом С.

Рис. 59

Эта форма используется в том случае, если повторяемое действие S выполняется при каждом значении некоторого параметра I (параметра цикла), изменяющегося в известных пределах с заданным шагом. При этом с самого начала известно число повторений цикла. Словесная запись цикла с параметром: для каждого значения параметра I, изменяющегося от А до В с шагом С, выполнять тело цикла S.