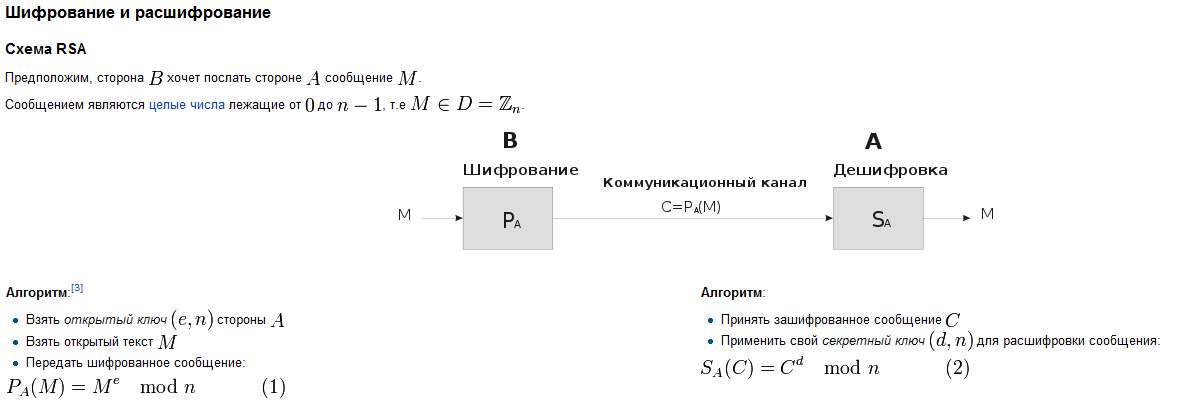
17.Криптосистема rsa.

RSA (буквенная аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом.

RSA стал первым алгоритмом такого типа, пригодным и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений.

Криптографические системы с открытым ключом используют так называемые необратимые функции, которые обладают следующим свойством:

В основу криптографической системы с открытым ключом RSA положена задача умножения и разложения составных чисел на простые сомножители, которая является вычислительно однонаправленной задачей.

В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). Каждый ключ — это часть информации. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями образуют «согласованную пару» в том смысле, что они являются взаимно обратными

Алгоритм создания открытого и секретного ключей:

1.Выбираются два различных случайных простых числа p и q заданного размера (например, 1024 бита каждое).

2.Вычисляется их произведение n = pq, которое называется модулем.

3.Вычисляется значение функции Эйлера от числа n:

φ(n) = (p − 1)(q − 1).

4.Выбирается целое число e (1 < e < φ(n)), взаимно простое со значением функции φ(n). Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257 или 65537.

-Число e называется открытой экспонентой (англ. public exponent)

-Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в e.

-Слишком малые значения e, например 3, потенциально могут ослабить безопасность схемы RSA.[4]

5.Вычисляется число d, мультипликативно обратное к числу e по модулю φ(n), то есть число, удовлетворяющее условию:

или: de = 1 + kφ(n), где k — некоторое целое число.

-Примечание: Можно вычислять и так (e*d) mod ((p-1)*(q-1)) = 1. Результат операции i mod j — остаток от целочисленного деления i на j, то есть если имеем (d*3) mod 20 = 1. Значит d будет, например 7. (Может быть и другим, например 27).

-Число d называется секретной экспонентой.

-Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.

6.Пара e, n публикуется в качестве открытого ключа RSA (англ. RSA public key).

7.Пара d, n играет роль секретного ключа RSA (англ. RSA private key) и держится в секрете.

18. Криптосистема Рабина

– криптографический алгоритм с открытым ключом. Ее безопасность, как и у RSA, связана с трудностью разложения на множители.

Безопасность схемы Рабина опирается на сложность поиска квадратных корней по модулю составного числа. Сложность этого алгоритма аналогична проблеме разложения на множители.

Главным неудобством практического применения криптосистемы Рабина является то, что при расшифровке текста получается четыре различных сообщения. И нужно применить дополнительные усилия для нахождения истинного исходного текста.

Данный алгоритм был опубликован в январе 1979 Майклом О. Рабином. Криптосистема Рабина была первой асимметричной криптосистемой, для которой было доказано, что восстановление исходного текста от зашифрованного столь же трудно как факторизация больших чисел. Точнее, она связана с трудностью извлечения квадратного корня по модулю составного числа N = р • q. Эти две задачи эквивалентны, т. е. - зная простые делители числа N, мы можем извлекать квадратные корни по модулю N, - умея извлекать квадратные корни по модулю N, мы в состоянии разложить N на простые множители.

Как любая асимметричная криптосистема, система Рабина использует и открытый и закрытый ключи. Открытый ключ необходим для шифрования документов и может быть опубликован для всеобщего обозрения. Закрытый ключ должен быть известен только получателям зашифрованных сообщений.

Процесс генерации ключей следующий:

Выбираются два больших простых числа p и q, которые удовлетворяют условию . Такой специальный вид простых чисел сильно ускоряет процедуру извлечения корней по модулю р и q.

Тогда . n - открытый ключ. Числа p и q - закрытый ключ.

Для шифрования сообщения необходим открытый ключ n. Чтобы расшифровать зашифрованный текст нужны p и q.

Рассмотрим простой пример. Пусть p = 7 и q = 11, тогда n = 77. Открытый ключ, 77, публикуется для всеобщего обозрения, с помощью его шифруются сообщения. Закрытые ключи, 7 и 11, остаются известны только владельцу, и с помощью их расшифровываются сообщения. Такой выбор ключей – хорошо подходит для примера. Но плохой для практического использования, т.к. разложение на множители 77 тривиально.

Для шифрования используется только открытый ключ n. С помощью его исходный текст преобразовывается в зашифрованный. Для шифрования сообщения m нужно просто вычислить:

.

Таким образом, шифрование состоит из операции умножения по модулю N, что обеспечивает более высокую скорость шифрования, чем в RSA, даже если в последней выбирают небольшую шифрующую экспоненту.

В нашем примере. Пусть исходным текстом является m = 20. Тогда зашифрованным текстом будет:

.

Расшифрование в этом алгоритме более сложное. Для него нужен закрытый ключ p и q. Процесс выглядит следующим образом:

Сначала, используя алгоритм Эвклида, из уравнения находим числа y_p и y_q.

Далее, используя китайскую теорему об остатках, можно вычислить числа

.

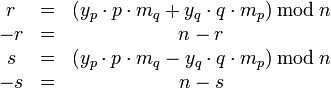Один из этих корней r, -r, s, -s является истинным открытым текстом m .

Вернемся в нашему примеру: В результате расшифровки получаем: . Видим, что один из корней является исходным текстом m.

Расшифровка текста кроме правильного приводит еще к трем ложным результатам. Это является главным неудобством криптосистемы Рабина и одним из факторов, которые препятствовали тому, чтобы она нашла широкое практическое использование.

Если исходный текст представляет собой текстовое сообщение, то определение правильно текста не является трудным. Однако, если сообщение является потоком случайных битов (например, для генерации ключей или цифровой подписи), то определение нужного текста становится реальной проблемой. Одним из способов решить эту проблему является добавление к сообщению перед шифрованием известного заголовка или некой метки.

Алгоритм Рабина похож на кодирование RSA, но вместо возведения сообщения в степень е при шифровании используется операция возведения блока сообщения в квадрат, что благоприятно сказывается на скорости выполнения алгоритма без ущерба криптостойкости.

Для декодирования китайская теорема об остатках применена вместе с двумя возведениями в степень по модулю. Здесь эффективность сопоставима RSA.

Выбор нужного текста из четырех приводит к дополнительным вычислительным затратам. И это послужило тому, что криптосистема Рабина не получила широкого практического использования.

Большое преимущество криптосистемы Рабина состоит в том, что случайный текст может быть восстановлен полностью от зашифрованного текста только при условии, что дешифровщик способен к эффективной факторизации открытого ключа n.

Криптосистема Рабина является доказуемо стойкой к атаке на основе подобранного открытого зашифрованного текста в рамках подхода “все или ничего”, тогда и только тогда, когда задача о разложении целого числа на простые множители является трудноразрешимой.

Стойкость по принципу “все или ничего” заключается в том, что, имея текст, зашифрованный определенным алгоритмом, атакующий должен восстановить блок исходного текста, размер которого, как правило, определяется параметром безопасности криптосистемы. Имея исходный и зашифрованный текст, атакующий должен восстановить целый блок секретного ключа. При этом атакующий либо добивается полного успеха, либо не получает ничего. Под словом «ничего» подразумевается, что атакующий не имеет никакой секретной информации ни до, ни после безуспешной атаки.

Криптосистема Рабина является абсолютно беззащитной перед атакой на основе выбранного шифротекста. Как правило, атакующий использует все имеющие у него возможности. Он вступает в контакт с атакованным пользователем, посылают ему зашифрованный текст для последующей расшифровки и требуют вернуть исходный текст.

К примеру, при добавлении избыточности, например, повторение последних 64 бита, можно сделать корень единственным. Алгоритм расшифрования в этом случае выдает единственный корень, который уже известен атакующему.

Процесс дополнительно уязвим, так как при кодировании используются только квадратные остатки. В примере при n = 77 только используется только 23 из 76 возможных состояний.