
- •1.Определение функции и способы ее задания.
- •2.Приближенные числа и действия с ними.
- •3.Предел последовательности.
- •4.Теоремы о пределах последовательностей.
- •5.Предел функции.
- •6.Теоремы о пределах функций.
- •7. Непрерывные функции и их свойства.
- •9. Производная функции.
- •10.Геометрический смысл производной.
- •12.Производная сложной функции.
- •14.Логарифмическая производная.
- •16.Теорема Ролля.
- •17.Теорема Лагранжа.
- •18.Правило Лопиталя.
- •21.Экстремум функции.
- •22.Наибольшее и наименьшее значения функции на отрезке.
- •23.Формулы Тейлора и Маклорена.
- •24.Комплексные числа и действия с ними.
- •25.Разложение рациональной функции на простейшие дроби.
- •26.Неопределенный интеграл и его свойства.
- •27.Замена переменной в неопределенном интеграле.
- •28.Интегрирование по частям.
- •29.Интегрирование рациональных дробей.
- •30.Интегрирование иррациональных выражений.
- •31.Интегрирование тригонометрических функций.
18.Правило Лопиталя.
В
математическом анализе правилом
Лопита́ля называют метод нахождения
пределов функций, раскрывающий
неопределённости вида
![]() и
и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
Точная формулировка
Правило
говорит, что если функции
![]() и
и
![]() обладают следующим набором условий:
обладают следующим набором условий:
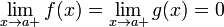 или
или
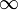 ;
;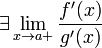 ;
;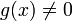 в
некоторой окрестности точки
в
некоторой окрестности точки
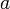 ,
тогда
существует
,
тогда
существует
![]() .
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
.
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
Доказательство
Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида
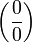 )
)
Поскольку
мы рассматриваем функции
![]() и
и
![]() только в правой проколотой полуокрестности
точки
,
мы можем непрерывным образом их
доопределить в этой точке: пусть
только в правой проколотой полуокрестности
точки
,
мы можем непрерывным образом их
доопределить в этой точке: пусть
![]() .
Возьмём некоторый
.
Возьмём некоторый
![]() из рассматриваемой полуокрестности и
применим к отрезку
из рассматриваемой полуокрестности и
применим к отрезку
![]() теорему
Коши. По этой теореме получим:
теорему
Коши. По этой теореме получим:
![]()
Но
,
поэтому
![]() .
.
Дальше, записав определение предела отношения производных и обозначив последний через А, из полученного равенства выводим:
![]() для
конечного предела и
для
конечного предела и
![]() для
бесконечного,
для
бесконечного,
что является определением предела отношения функций.
Докажем теорему для неопределённостей вида
 .
Пусть,
для начала, предел отношения производных
конечен и равен А.
Тогда, при стремлении
к
справа,
это отношение можно записать как
.
Пусть,
для начала, предел отношения производных
конечен и равен А.
Тогда, при стремлении
к
справа,
это отношение можно записать как
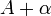 ,
где
,
где
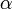 —
O(1). Запишем это условие:
—
O(1). Запишем это условие:
![]()
Зафиксируем
![]() из отрезка
из отрезка
![]() и применим теорему Коши ко всем
из
отрезка
и применим теорему Коши ко всем
из
отрезка
![]() :
:
![]() ,
что можно привести к следующему виду:
,
что можно привести к следующему виду:
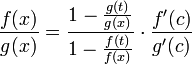
Для
,
достаточно близких к
,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как
![]() и
и
![]() —
константы, а
и
стремятся
к бесконечности). Значит, этот множитель
равен
—
константы, а
и
стремятся
к бесконечности). Значит, этот множитель
равен
![]() ,
где
,
где
![]() —
бесконечно малая функция при стремлении
к
справа. Выпишем определение этого факта,
используя то же значение
—
бесконечно малая функция при стремлении
к
справа. Выпишем определение этого факта,
используя то же значение
![]() ,
что и в определении для
:
,
что и в определении для
:
![]()
Получили,
что отношение функций представимо в
виде
![]() ,
и
,
и
![]() .По любому данному
можно
найти такое
.По любому данному
можно
найти такое
![]() ,
чтобы модуль разности отношения функций
и
,
чтобы модуль разности отношения функций
и
![]() был
меньше
,
значит, предел отношения функций
действительно равен
.
был
меньше
,
значит, предел отношения функций
действительно равен
.
Если же предел бесконечен (допустим, он равен плюс бесконечности), то
![]() .
.
В
определении
будем
брать
![]() ;
первый множитель правой части будет
больше 1/2 при
,
достаточно близких к
,
а тогда
;
первый множитель правой части будет
больше 1/2 при
,
достаточно близких к
,
а тогда
![]() .
.
Для других баз доказательства аналогичны приведённым.
Примеры
![]()
![]()
Здесь
можно применить правило Лопиталя 3 раза,
а можно поступить иначе. Можно разделить
и числитель, и знаменатель на x в наибольшей
степени(в нашем случае
![]() ).
В этом примере получается:
).
В этом примере получается:
![]()
![]()
![]()
21.Экстремум функции.
Определение экстремума
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) > 0 (f ' (x) < 0).
Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Точки экстремума
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную
f ' (x) в окрестности точки xо и вторую производную f”(x0) в самой точке xо. Если f ' (xо) = 0, f”(x0) >0 (f”(x0) <0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же f”(x0) =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Пример 3.22. Найти экстремумы функции f(x) = 2x3 - 15x2+ 36x - 14.
Решение. Так как f '(x) = 6x2 - 30x +36 = 6(x -2)(x - 3), то критические точки функции x1 = 2 и x2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x2 = 3 производная меняет знак минус на плюс, поэтому в точке x2 = 3 у функции минимум. Вычислив значения функции в точках
x1 = 2 и x2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
