12.Производная сложной функции.

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а - целая рациональная функция (смотрите классификацию элементарных функций), тогда .

В свою очередь, g(x) также может быть сложной функцией. Например, .

Условно такое выражение можно обозначить как . Здесь f – функция синуса, f₁ - функция извлечения квадратного корня,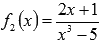 - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции. .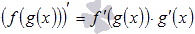

14.Логарифмическая производная.

Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: .

Используя формулу производной сложной функции, найдем, что

.

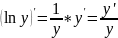Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.

Пример

Логарифмическая производная функции имеет экономический смысл – отношение скорости изменения величины у (ее производной) к самой этой величине – темп изменения у; если темп положителен – скорость изменения увеличивается, если отрицателен – скорость падает.

16.Теорема Ролля.

Теорема Ро́лля утверждает, что если функция, имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала.

Формулировка Пусть дана непрерывная функция на отрезке , и для любого существует конечная или бесконечная производная . Тогда если , то

Следствия

-Многочлен -ой степени может иметь не более различных корней.

- Если многочлен степени выше второй имеет ровно различных корней, то его производная имеет ровно корень.

17.Теорема Лагранжа.

Теорема. Пусть функция дифференцируема в открытом промежутке и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка , что (1)

Доказательство. Рассмотрим вспомогательную функцию

Эта функция непрерывна и дифференцируема в промежутке , а на его концах принимает одинаковые значения:

Тогда удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка , в которой производная функции равна нулю:

Следствие 1. В частном случае, когда , из теоремы Лагранжа вытекает, что существует точка , в которой производная функции равна нулю: . Это означает, что теорема Лагранжа является обобщением теоремы Ролля.

Следствие 2. Если во всех точках некоторого промежутка , то в этом промежутке.

Действительно, пусть и – произвольные точки промежутка и . Применяя теорему Лагранжа к промежутку , получим

Однако во всех точках промежутка . Тогда

Учитывая произвольность точек и , получаем требуемое утверждение.

Геометрическая интерпретация теоремы Лагранжа. Разностное отношение в правой части формулы (1) есть угловой коэффициент секущей, проходящей через точки и а производная равна угловому коэффициенту касательной к графику функции в некоторой средней точке промежутка . Поэтому за теоремой Лагранжа закрепилось название “теорема о среднем”.

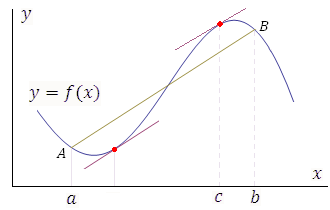
Рис. 6. Теорема Лагранжа устанавливает условия существования хотя бы одной точки c, в которой касательная к графику функции параллельна секущей AB. Таких точек может быть несколько.

Физическая интерпретацию теоремы Лагранжа. Пусть функция описывает смещение частицы из начального положения в зависимости от времени x ее движения по прямой. Тогда разностное отношение

представляет собой среднюю скорость движения частицы за промежуток времени , а производная – мгновенную скорость движения частицы в момент времени c. Существует такой момент времени, в который мгновенная скорость движения равна средней скорости.

Отметим, что формула (1) сохраняет свою справедливость и при b < a. Если применить теорему Лагранжа к промежутку и представить значение c в виде

где то формула (1) примет вид

(2)

Равенство (2) дает точное значение для приращения функции при конечном значении приращения аргумента и называется формулой конечных приращений. Единственным недостатком этой замечательной формулы является присутствие в ней неопределенного числа θ.