10.Геометрический смысл производной.

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

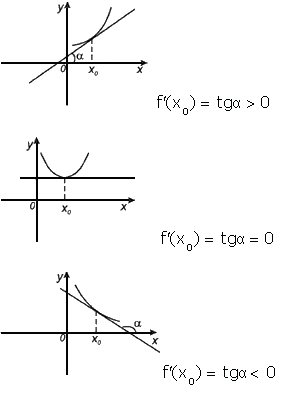
Рассмотрим график функции y = f ( x ):

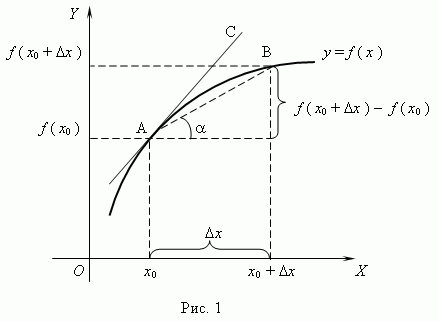
Из рис.1 видно, что для любых двух точек A и B графика функции: , где 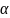- угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей.

Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.

Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.

Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

11.Правила дифференцирования.

Пусть заданы две функци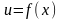и и 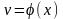, которые имеют про­из­вод­ные в точке .

1. Производная алгебраической суммы равна алгебраической сумме производных. .

Покажем это. Пусть некоторая функция у, равная имеет приращение . Тогда функции и тоже должны получить приращения и , соответственно. Новое значение будет , а для – , следовательно,

Найдем по определению (2) производной

.

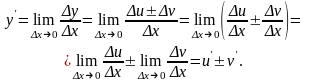2. Производная произведения равна . Покажем спра­вед­ли­вость этого равенства.

Если, как в первом случае, дать приращение , то функции u и v также получат приращение, следовательно, и функция тоже изменится. Найдем .

.

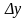По определению производной

Если необходимо вычислить производную нескольких сомножителей, например, , если все три функции имеют производные в точке , используя правило вычисления производной для двух сомножителей, получим

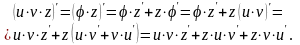
3. Производная частного. Рассмотрим функцию , причем, кроме су­щес­твования производных в точке для функций и необходимо по­ло­жить, что 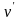в точке отлична от нуля.

Найдем .

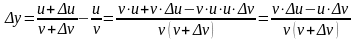
и тогда из определения производной имеем

.

Пример. Показать, что .

Решение. Используя производную частного

4. Производная сложной функции. Пусть дана 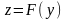, где 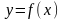. Тогда имеет место теорема, которую приведем здесь без доказательства.

Теорема. Если функция имеет в точке производную и функция имеет в точке 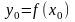производную 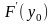, тогда сложная функция имеет в точке производную, равную

(3)

Пример. Найти производную функции .

Решение. .

Пример. Найти производную функции .

Решение.

Пример. Найти производную сложной функции .

Решение.

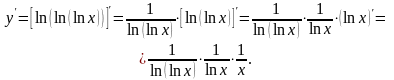
5. Логарифмическое дифференцирование. Пусть дана функция . При этом предполагается, что функция не обращается в нуль в точке . Покажем один из способов нахождения производной функции , если очень сложная функция и по обычным правилам диф­фе­рен­цирования найти производную затруднительно.

Так как по первоначальному предположению не равна нулю в точке, где ищется ее производная, то найдем новую функцию и вычислим ее производную

. (4)

Отношение 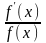называется логарифмической производной функции . Из формулы (4) получаем

. (5)

Формула (5) дает простой способ нахождения производной функции .

6. Производная обратной функции.

Теорема. Если имеет в точке производную, отличную от нуля, тогда в этой точке обратная функция также имеет производную и имеет место соотношение

. (6)

Пользуясь этой теоремой, найдем производные обратных три­го­но­мет­ри­чес­ких функций.

1. 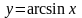на интервале . , тогда , от­ку­да сле­до­ва­тель­но, .

2. . . 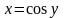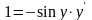, откуда

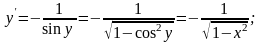
3. 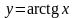. ; , откуда

4. ; ;

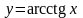5. , где и являются функциями от . Для нахождения применим формулу (5). Для этого предварительно найдем функцию

и ее производную

.

По формуле (5) получаем .

Эту же формулу можно получить иначе. Представим в виде

и найдем производную этой функции

.