7. Непрерывные функции и их свойства.

Свойства непрерывных функций

Теорема 1. Сумма непрерывных функций есть функция непрерывная.

Доказательство. Пусть функции и непрерывны в точке a. Тогда

Согласно свойству пределов функций существование пределов функций и гарантирует существование предела их суммы. При этом что и требовалось доказать.

Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная.

Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Теорема 2. Произведение непрерывных функций есть функция непрерывная.

Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная.

Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль.

Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю.

Теорема 4. Любая элементарная функция непрерывна в области своего определения.

Для доказательства этой теоремы нужно показать, что для любого числа a из области определения элементарной функции выполняется условие

Продемонстрируем справедливость теоремы на некоторых конкретных примерах.

1. Пусть , где n – целое положительное число. Тогда

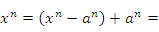
Первый член в правой части этого равенства представляет собой бесконечно малую функцию при x → a и, следовательно,

Покажем, что показательная функция является непрерывной в каждой точке a. Действительно,

Теорема 5. Пусть функция непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой . Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами, принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение. Отметим, что теорема 5 лежит в основе численных методов решения уравнений.

9. Производная функции.

Определение. Если отно­ше­ние имеет предел при этот предел называ­ют производной функции при заданном значении и за­пи­сывают

. (1)

Замечание. Если при не­ко­то­ром значении , су­щест­ву­ет производная функции при этом значении, то в этой точке функция непрерывна.

Заметим, что отношение из рис. 1 численно равно .

Определение. Производная функции в точке численно равна тан­генсу угла, который составляет касательная к графику этой функции по­строенной в точке с положительным направлением с осью .

Из последнего определения ста­но­вится ясно, почему в случае убы­ва­ю­щей функции (рис. 2) про­из­вод­ная от­ри­цательна. Это объясняется тем, что , если будет отрицатель­ным.

На этом свойстве производной осно­ва­но исследование поведения функции на возрастание (убывание) на заданном отрезке.