30.Интегрирование иррациональных выражений.
Найдём определённый интеграл от иррационального выражения
Приме́ним подстановку t² = (x − 3)/(x − 2)
Тогда t²·(x − 2) = x − 3; (t² − 1)·x = 2·t² − 3
x = (2·t² − 3)/(t² − 1) = 2 − 1/(t² − 1); dx = 2·t·dt/(t² − 1)
Пределы интегрирования:
нижний t₁ = √((3 − 3)/(3 − 2)) = 0
верхний t₂ = √((4 − 3)/(4 − 2)) = 1/√2
После избавления от иррациональности получили интеграл от рациональной дроби. Разложим дробь в сумму элементарных дробей методом неопределённых коэффициентов Лагранжа.
A·(t² − 1) + B·(t² + 1) = t² ⇒ A = B = ½
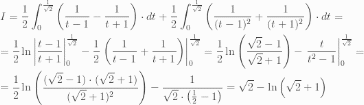
31.Интегрирование тригонометрических функций.
1.Интегралы
вида
вычисляются
преобразованием произведения
тригонометрических функций в сумму по
формулам:
Например,
2.Интегралы
вида
,
где m или n– нечетное положительное
число, вычисляются подведением под знак
дифференциала.
Например,
3.Интегралы вида , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени:
Например,
4.Интегралы
где
, вычисляются заменой переменной:
или
Например,
