3. Графическое определение предельного времени отключения.

Из рис.1.23 имеем:

Так как предельное время отключения КЗ меньше времени отключения КЗ, то в системе нарушается синхронная динамическая устойчивость.

Для избегания нарушения синхронной динамической устойчивости необходимо принять дополнительные меры по устранению асинхронного режима, а именно установить более быстродействующую релейную защиту или установить устройства АПВ на данных линиях или установить устройство АРВ на СГ.

Раздел II Оценка статической устойчивости ээс на основе анализа характеристического уравнения.

2.1 Составление схемы замещения для нормального режима работы.

Генератор представляем синхронными параметрами.

Рис.2.1. Схема замещения ЭЭС нормального режима работы с представлением генератора синхронными параметрами.

Для определения взаимного угла между векторами ЭДС генератора и напряжением на шинах системы используем программу RRSWIN1. Для этого в программе RRSWIN1 задаем генератор синхронными параметрами, а остальные параметры определены в 1 разделе, и регулируем угол δ до тех пор, пока активная мощность генератора P_Г0 не совпадет c P₂.

Рис.2.2. Схема замещения ЭЭС в программе RRSWIN1 для определения угла синхронной ЭДС.

Получим:

Таблица 2.1 Исходный режим ЭЭС.

	PГ0	Q’Г0	I0	UГ0	Eq0	E’q0
EQ0=2.729; δ0=56.1°	0.83	2.467	0.954	1.0	2.729	1.016

2.2 Определение собственных и взаимных проводимостей.

Для определения собственных и взаимных проводимостей представляем генератор синхронными параметрами и используем программу RRSWIN1.

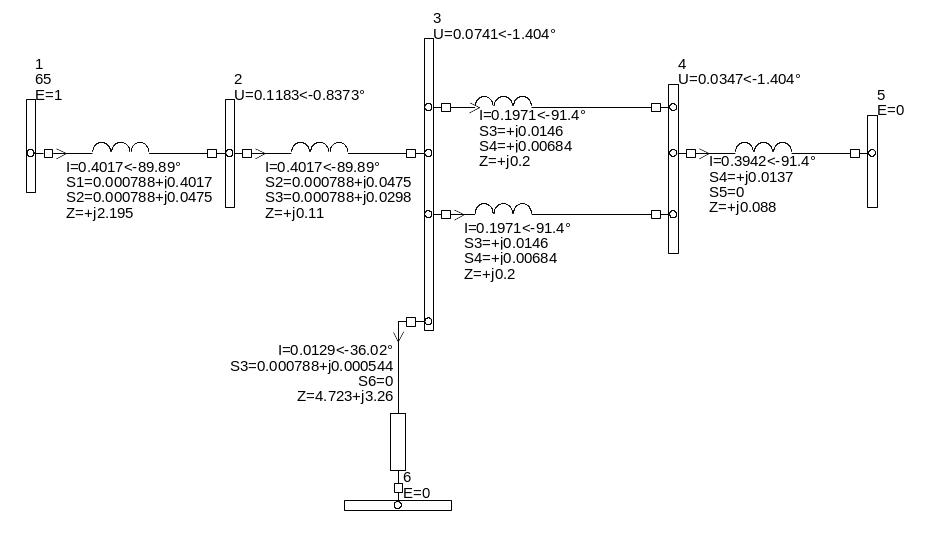
Рис.2.3. Схема замещения ЭЭС в программе RRSWIN1 для определения собственных и взаимных проводимостей.

Определяем отклонение аргументов:

Рассчитываем в RRS два режима ЭЭС при поочередных малых отклонениях аргументов и результаты сводим в таблицу 2.2.

Рис. 2.4 Результаты расчета при вариации

_{Рис. 2.5 Результаты расчета при вариации}

Таблица 2.2 Параметры варьируемых режимов.

Аргументы	Рг	Q`г	I	Uг	Eq	E'q
EQ =2.865 δ0=56.1	0.872	2.746	1.006	1.013	2.865	1.049
EQ0 =2.729 δ=58.91	0,855	2.508	0,971	0.989	2.729	1.206

Вычисляем приращения режимных параметров вычитанием строк таблицы 2.1 из строк таблицы 2.2.

Таблица 2.3 Приращения параметров.

Аргументы	ΔРг	ΔI	ΔUг	ΔEq	ΔE'q
ΔEQ =0.137	0,042	0,052	0,013	0,136	0,033
Δδ=2.81=0.049 рад	0,025	0,017	-0,011	0	-0,19

Вычисляем частные производные, например:

Дальнейшие расчеты сводим в таблицу 2.4

Таблица 2.4. Значения частных производных

Аргументы	∂Рг	∂I	∂Uг	∂Eq	∂E'q
∂EQ	0,306	0,379	0.095	0.993	0,241
∂δ	0.857	0.346	-0.224	0	-3.877

Столбцы этой таблицы соответствуют функциям, а строки аргументам.