3.1.2 Реакція схеми на сигнал прямокутної форми.

У бібліотеці програмованих джерел виберемо закладку PulseSource. Подаємо на вхід схеми сформований сигнал і проводимо аналіз в часовій області (Аlt+l). Вихідні осцилограми реакції схеми на прямокутній сигнал показані на рис. 8.

Рис. 7 Задання параметрів розрахунку ПП

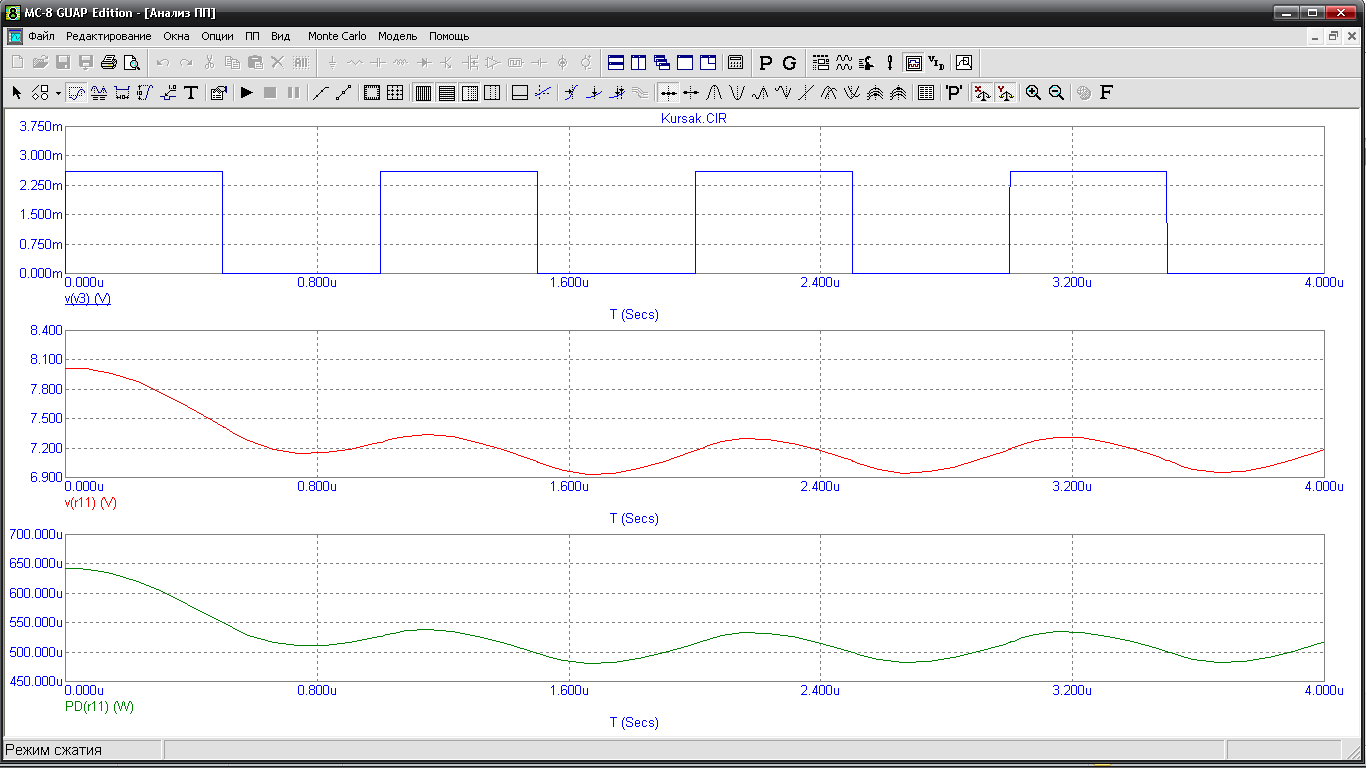
Рис. 8 Осцилограми імпульсу на вході, виході та потужність виділена на опорі навантаження.

3.1.3 Реакція схеми на імпульсну характеристику.

У бібліотеці програмованих джерел виберемо закладку PulseSource і створимо імпульсне джерело сигналу IMPULSE. Подаємо на вхід схеми сформований сигнал і проводимо аналіз в часовій області (Аlt+l). Вихідні осцилограми реакції схеми на прямокутній сигнал показані на рис. 10.

Рис.9 Задання параметрів розрахунку ПП

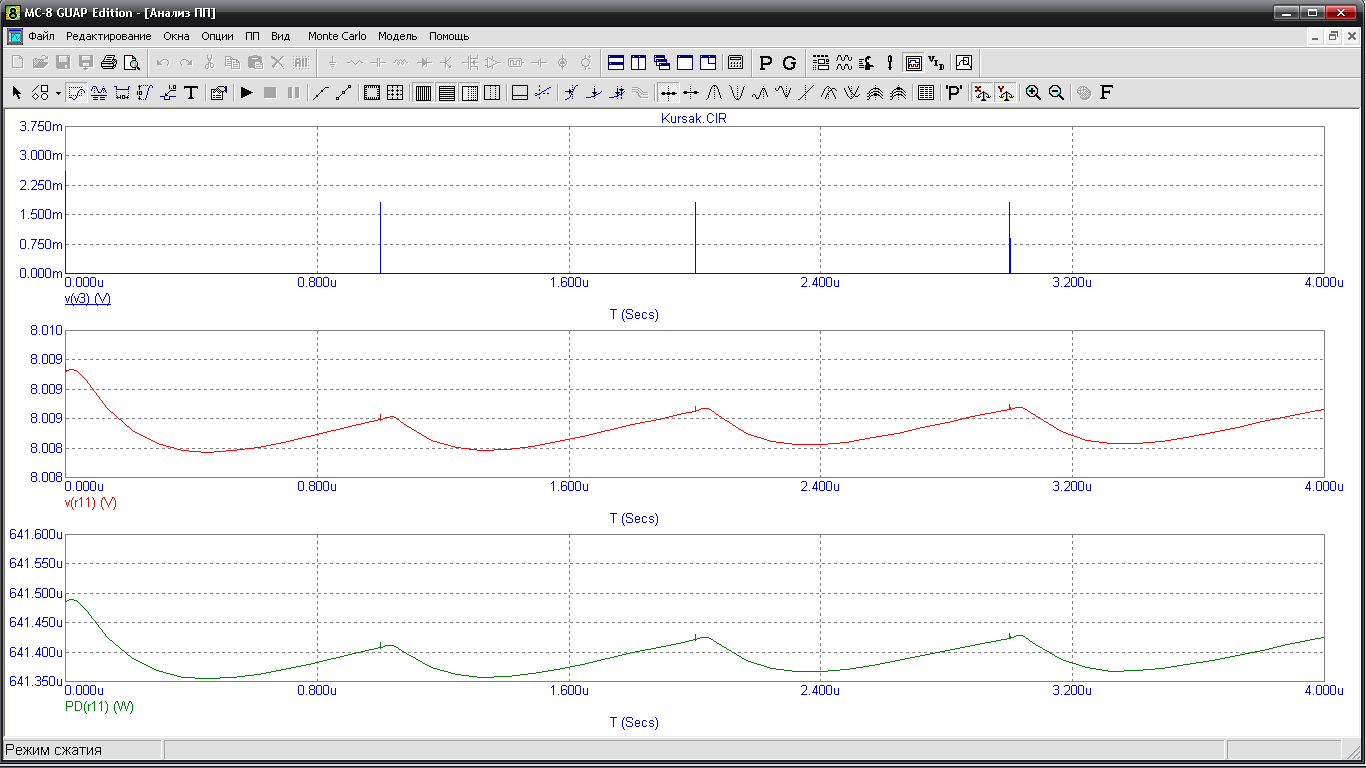
Рис. 10 Осцилограми імпульсу на вході, виході та потужність виділена на опорі навантаження.

4.1 Проведення частотного аналізу схеми

4.1.1Виведення АЧХ і ФЧХ схеми

Для проведення частотного аналізу схеми фільтра використаємо вже створене джерело синусоїдального форми. Заходимо на панелі інструментів в меню «Аналіз», вибираємо пункт «Частотні характеристики» (рис.11).

Рис.11. Ввімкнення аналізу частотних характеристик схеми

У вікні розрахунку частотних характеристик (рис.12) задаємо діапазон частот від 0,1 Гц до 100 МГц та температуру 27°С . Щоб вивести на екран у верхньому полі осцилограму АЧХ потрібно в колонці виводу графіка поставити 1 і ввести вираз для осі Y->db

Аналогічно виводимо графік ФЧХ у нижньому полі екрану. В колонці виводу графіка ставимо 2 і вводимо вираз для змінної Y->ph.

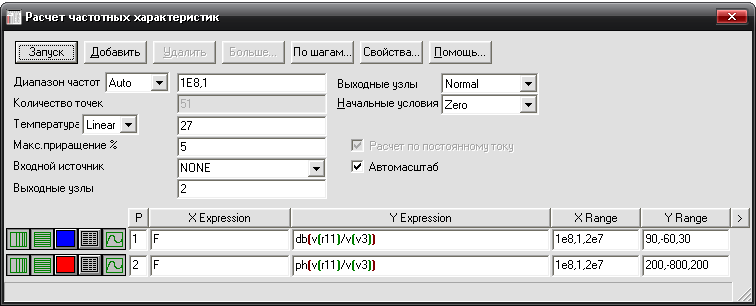
Рис.12. Розрахунок частотних характеристик

Отримаємо графіки АЧХ та ФЧХ при температурі 27°С :

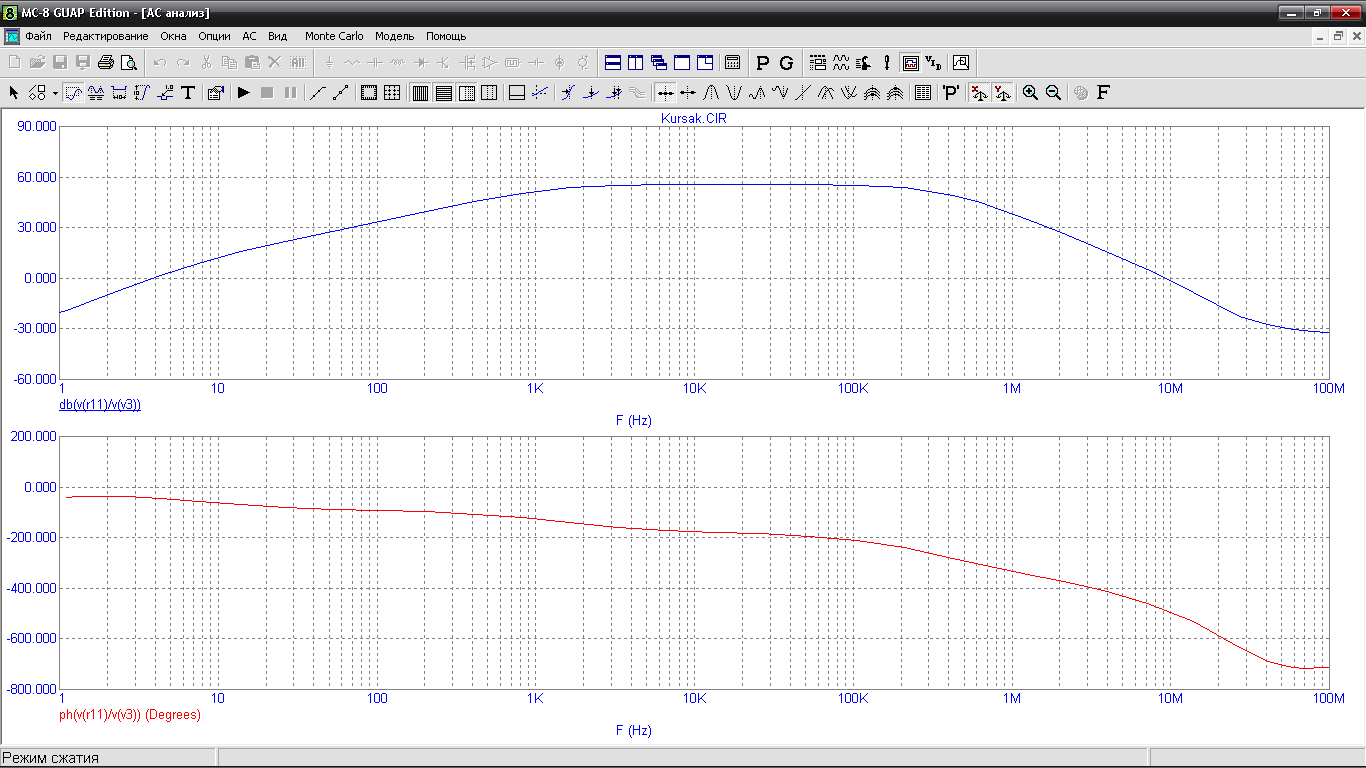
Рис.13. АЧХ та ФЧХ досліджуваної схеми

Визначення частот нижнього та верхнього зрізу, та ширину смуги пропускання

З графіка видно, що:

частота нижнього зрізу – 3.5кГц

частота верхнього зрізу – 100кГц

ширину смуги пропускання – 96.5 кГц

Ці дані не задовільняють технічні умови тому приймається рішення змінити ємність вхідного конденсатора на ємність 220nF. Ми отримуємо результат на рис 13.1

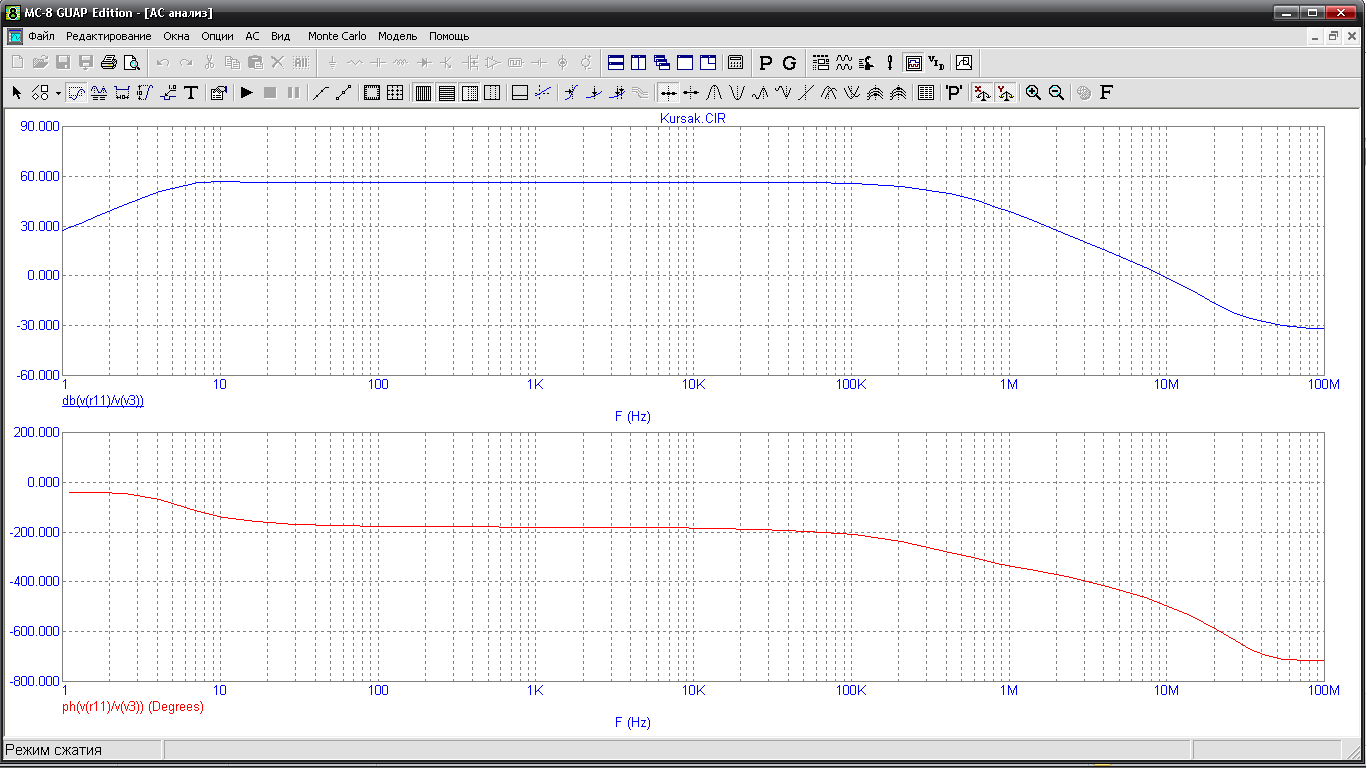Рис 13.1 АЧХ та ФЧХ відкоректованої схеми

З графіка видно, що:

частота нижнього зрізу – 15Гц

частота верхнього зрізу – 100кГц

ширину смуги пропускання – 99.85 кГц

Це цілком задовольняє умови поставленої ТЗ

4.1.2 Дослідження відносної зміни характерних точок ачх та фчх при зміні температури

Визначимо відносну зміну характерних точок АЧХ і ФЧХ у діапазоні зміни температур від -50С⁰ до +50С⁰. Для цього всі елементи схеми зробимо температурно залежними. Як приклад покажемо це на резисторі R2. Відкриваємо подвійним клацанням л.к. миші на резисторі R2 вікно задання параметрів виберимо пункт MODEL= та вибираємо зі списку потрібну температурну модель резистора, що є у базі даних програми. Всі наступні елементи будемо зрівнювати таким же чином. Температурну модель елементів можна також створити самому, заповнивши потрібні значення нижніх пунктів. Заходимо в частотний аналіз (Аlt+2), вказуємо діапазон зміни температури таким чином "50,-50,10" , що означає зміну температури від -50 до 50 °С з кроком 10°С і запускаємо аналіз. Графіки АЧХ та ФЧХ наведені на рис.14.

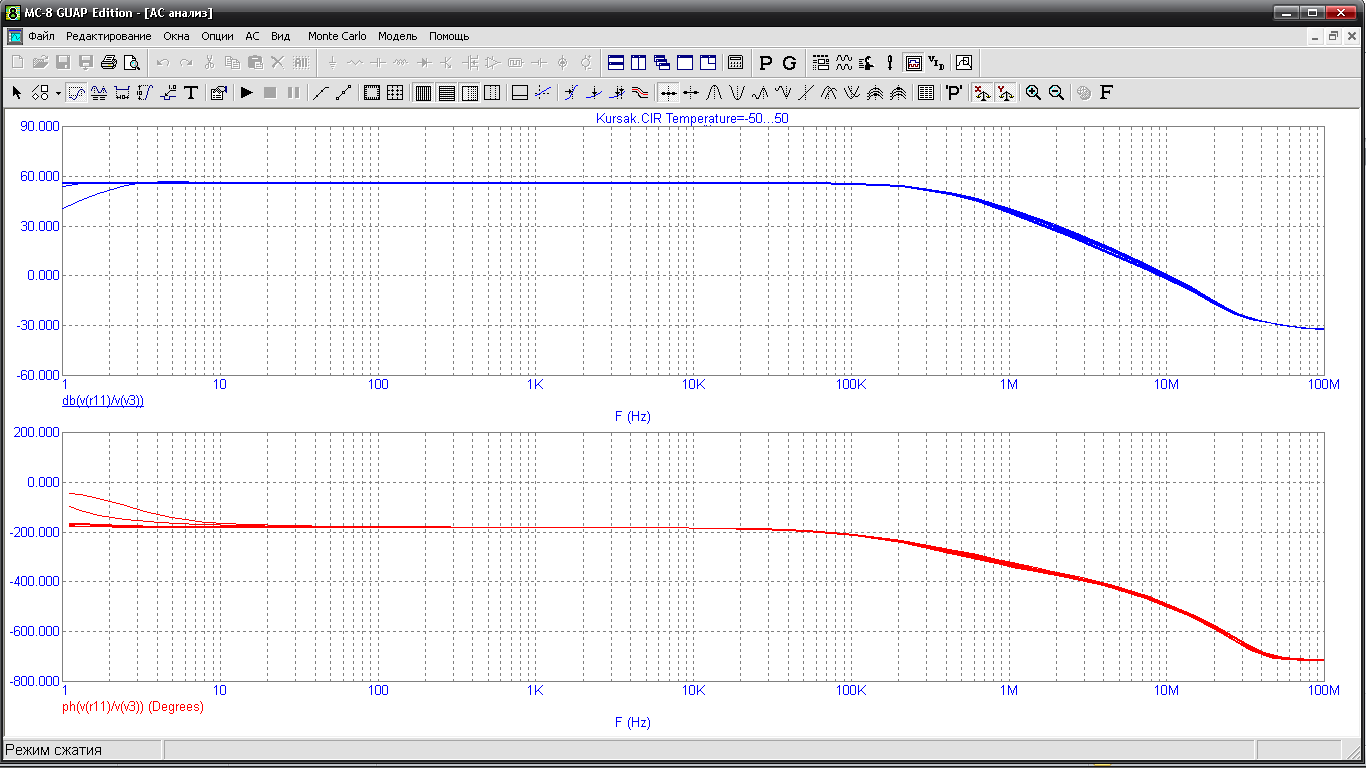
Рис.14. Температурний вплив на АЧХ і ФЧХ

4.1.3. Дослідження відносної зміни характерних точок АЧХ та ФЧХ при зміні параметра елементів схеми

Дослідимо відносну зміну характерних точок АЧХ і ФЧХ при зміні параметра одного пасивного елемента. Дослідимо як зміняться АЧХ та ФЧХ при зміні параметра відповідного елемента при змінійого номінального значення.

Розглянемо зміну параметрів найбільш впливових елементів резистора. Спочатку змінюємо резистор R9. Для цього в меню розрахунку частотних характеристик схеми виберемо пункт «По крокам» (рис.15).

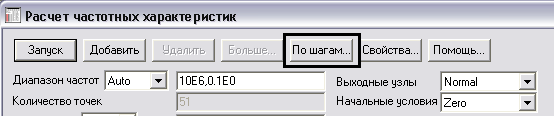
Рис.15. Ввімкнення по крокової зміни параметрів елементів.

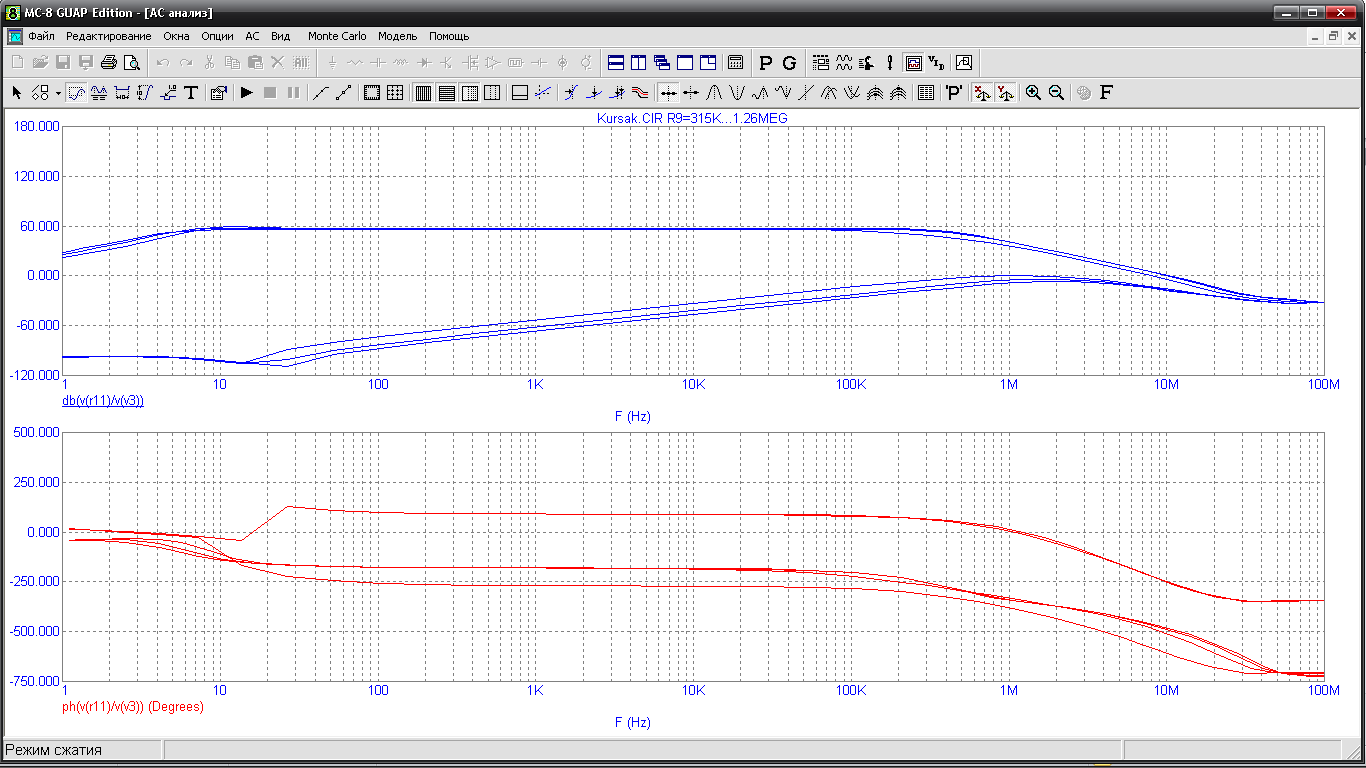
Рис.16. Зміна АЧХ та ФЧХ при зміні параметра резистора R2

4.2 Аналіз роботи схеми за методом Монте Карло

Метод Монте Карло дозволяє оцінити роботу пристрою при заданих параметрах розкиду елементів схеми. Це варіант статистичного оцінювання, прогнозування, імітації роботи схеми при не ідеальності технології виконання елемента. За цим методом можна отримати найгірший випадок роботи схеми або всі варіанти реакції схеми при заданому розкиді та числу експериментів.

Застосуємо метод Монте-Карло для найгіршого випадку роботи схеми, як в часовій так і в частотній області дослідження схеми. Аналогічно як при дослідженні температурної залежності схеми визначимо для всіх елементів їх моделі. Тепер в часовому режимі заходимо в закладку "MonteCarlo/Опції", де заповнюємо відповідні графи (рис.17).

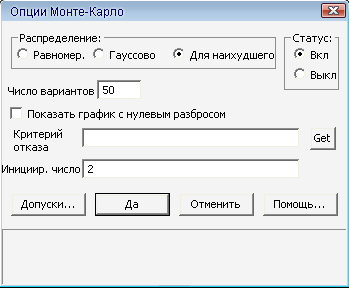
Рис.17. Вікно опцій методу Монте-Карло

Результати використання методу Монте-Карло при дослідженні в часовій області схеми показані на рис.18.

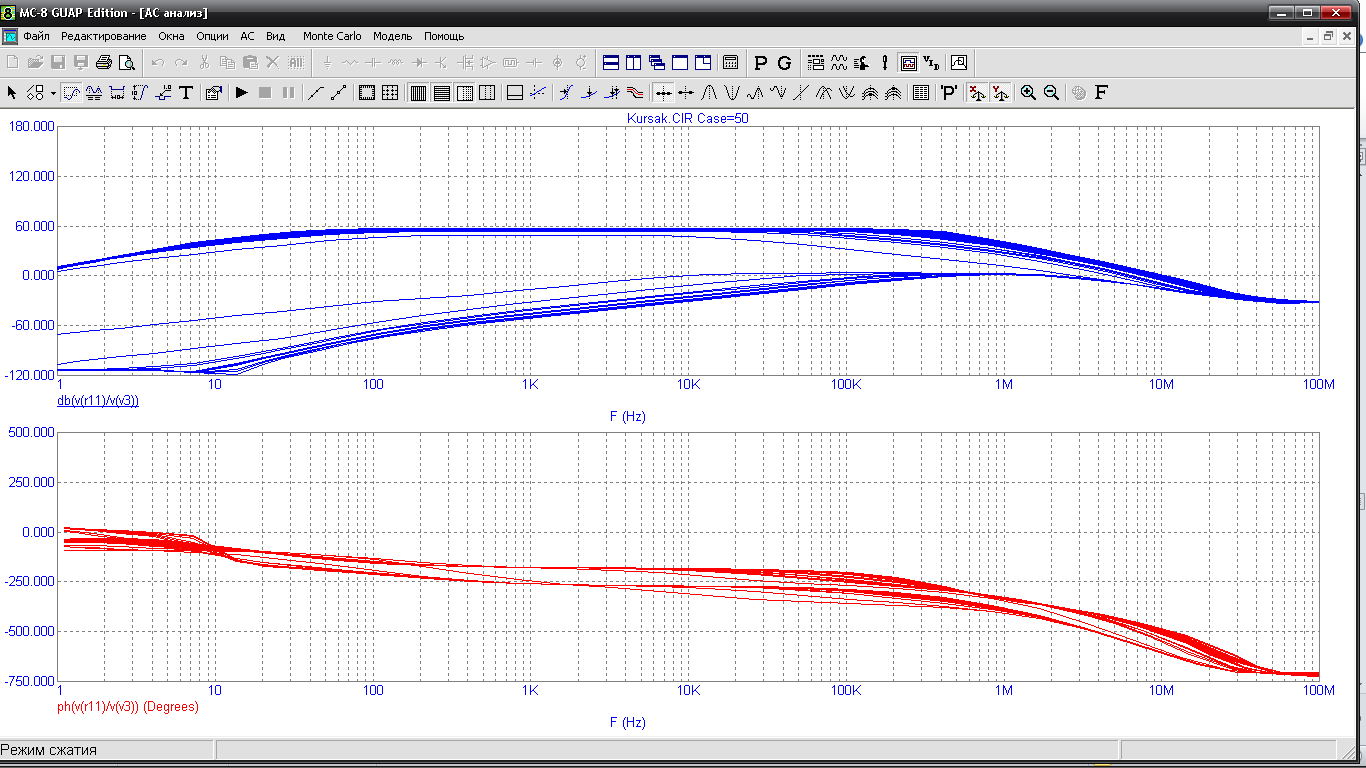Рис.18. АЧХ та ФЧХ при випадковій зміні параметрів елементів у схемі методомнайгіршого випадку.

Список використаної літератури

1. Амелина М. А., Амелин С. А., Програма схемотехнического моделирования Micro-Cap 8 – М.: Горячая линия – Телеком 2007. – 464с.

2. Николаєв А. П., Малкина М. В., 500 схем для радиолюбителей часть третья. Усилители НЧ и усилительно – комутационные устройства. Приставки к усилителям. УФА 1998. – 146с.

3. М.А. Амелина“ Конспект лекций по курсу „Компьютерный анализ и синтез электронных устройств”

4. Разевиг.В.Д. Система проектированияOrCad 9.2. – М.: Солон-Р, 2001.

5. Попов В.П. Основытеориицепей. – М.: Высш. шк., 1985.