8.3. Узагальнена формула Вейсбаха для місцевих втрат.

В загальному випадку місцеві втрати характеризуються звуженням перерізу транзитного потоку і появою циркуляційних областей. А втрата напору h_j обумовлена, головним чином, на віддалі за стисненим перерізом С-С.

Наприклад, на рис. 8.4. показані епюри швидкостей і область існування місцевих втрат при обтіканні засувки транзитним потоком.

Тому Вейсбахом було запропоновано подавати втрату напору для довільного випадку при місцевому опорі у виді:

(8.5)

де - коефіцієнт опору при місцевих втратах; під слід розуміти коефіцієнт стиснення потоку.

Коефіцієнт визначається експериментальним шляхом для кожного виду місцевих опорів, в першу чергу він визначається геометрією опорного вузла.

8.5. Повний коефіцієнт опору.

Н

ехай маємо трубу з коліном, засувкою і з різкою зміною перерізу. Будемо вважати, що віддаль між перешкодами велика (більша 20 ÷ 30 D). Тоді місцеві втрати обраховуються окремо і складуються в суму:

Згадаємо формулу Дарсі для втрат напору по довжині:

Введемо позначення і назвемо цей вираз коефіцієнтом опору по довжині

Тоді повна втрата напору за пропозицією Вейсбаха записуються так:

, (8.6)

де - повний коефіцієнт опору.

8.6. Приклади розрахунку коротких трубопроводів.

Якщо при розрахунках довгих трубопроводів місцевими втратами можна знехтувати, то при довжинах міських водонапірних мереж менших 200 м місцеві втрати складають вже ≈5%, тому в таких випадках необхідно враховувати як h_l так і ∑h_j .

Витік рідини під рівень. Нехай маємо встановлений рух, швидкість υ

н

езмінна в часі. Різниця між рівнями в посудинах А і В, які з’єднані трубопроводом – z = const ( випадок, коли в посудину А рідина постійно додається, а з посудини В – відводиться.

Знайдемо величину витрати Q для трубопроводу.

Для цього використаємо рівняння Бернуллі для двох

перерізів 1-1 і 2-2. Проведемо площину порівняння на рівні поверхні другого резервуара.

Виконаємо деякі припущення і приведення вхідних величин:

1. коефіцієнт корекції приймемо ;

2.

Різниця рівнів витрачається на втрати у трубопроводі. h_f знайдемо через повний коефіцієнт опору ξ_f :

Тоді витрата рідини

(8.7)

Випадок витікання рідини в атмосферу. (див. рис. 8.6).

Р

івняння Бернуллі для двох перерізів дає такий вираз:

Втрати напору через коефіцієнт опору:

Витрата рідини (8.8)

Кінцеві формули, які ми отримали, часто використовуються на практиці, при цьому логічним виглядить введення коефіцієнта витрати трубопроводу μ_т:

;

8.7. Розрахунок довгих трубопроводів.

Витікання під рівень. У випадку довгого трубопроводу, коли втрати напору по довжині набагато більші ніж місцеві, останніми можна знехтувати. При цьому п’єзометрична лінія Р-Р співпадає з напірною лінією Е-Е.

Чим більша швидкість рідини в трубі, тим більша втрата напору, а це значить і більший п’єзометричний нахил J. Згадаємо, що величина J характеризує падіння п’єзометричної лінії, віднесеної до відповідної елементарної довжини струменю:

Р

озглянемо з’єднання двох резервуарів трьома трубами різних діаметрів і довжин.

Очевидно, що висота напору дорівнює сумі втрат напорів на кожній ділянці трубопроводу:

Втрати на окремій ділянці виразимо з допомогою формули Шезі:

Тоді 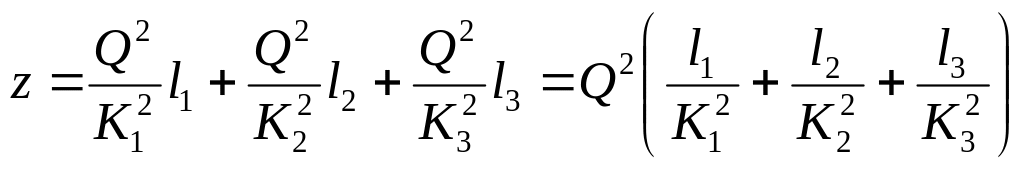(8.9)

Звідси витрата рідини:

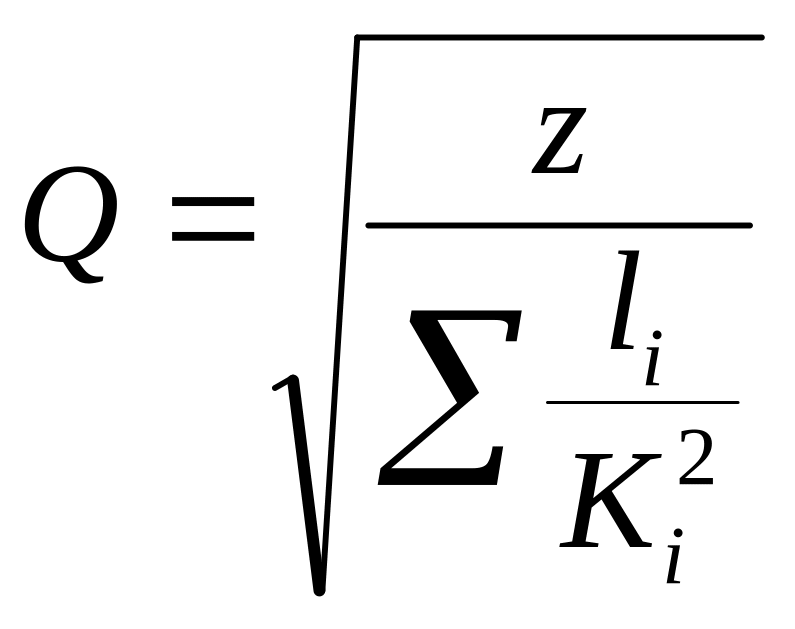(8.10)

Використовуючи формули (8.9) і (8.10) можна рішати різні практичні задачі. Наприклад: якщо відомо z і дані трубопроводу (l,ω) можемо обрахувати Q; або відомо Q, l, ω – знайти висоту потенційного напору z.

Витік в атмосферу. Нехай маємо резервуар A, з якого через довгий трубопровід (l,d), що закінчується вихідним соплом (ω_о) , витікає рідина з

певною швидкістю υ_о (рис.8.8).

При довгих трубопроводах слід враховувати кінцеву втрату

Повний напір витрачається на

,

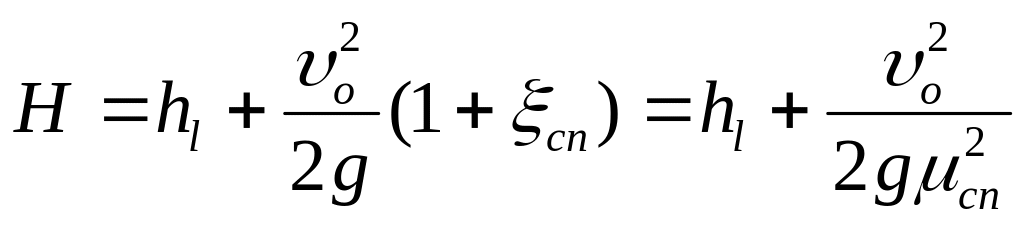де - коефіцієнт витрати сопла.

H можна подати через витрати потоку Q:

(8.11)

Вираз (8.11) дає можливість рішати такі задачі:

- відомі характеристики трубопроводу l, D, а також витрата Q – знайти H;

- відомо l, D і напір Н – знайти витрату Q;

- відомо Q, H, l – знайти діаметр трубопроводу (очевидно, що діаметр D зв’язаний з модулем витрати К).