6.2. Моделі онтології й онтологічної системи

Вище вже наголошувалося, що поняття онтології припускає визначення і використання взаємозв’язаної та взаємоузгодженої сукупності трьох компонентів: таксономії термінів, визна­чень термінів і правил їх опрацювання. Враховуючи це, введемо наступне визначення поняття моделі онтології.

Під формальною моделлю онтології О будемо розуміти впорядковану трійку такого вигляду:

О = <С, R, F>,

де С — скінченна множина концептів (понять, термінів) предметної області, яку задає онтологія О; R — скінченна множина відношення між концептами (поняттями, термінами) заданої предметної області; F — скінченна множина функцій інтерпретації (аксіоматизація), заданих на концептах чи відношеннях онтології О.

Зазначимо, що природним обмеженням, що накладається на множину С, є його скінченність і непустота. Інша справа з компонентами F і R у визначенні онтології О. Зрозуміло, що і в цьому випадку F і R мають бути скінченними множинами. Розглянемо окремі випадки, коли ці множини порожні.

Нехай R = Ø і F= Ø. Тоді онтологія О трансформується у простий словник:

О = V = <С, {}, {}>.

Така вироджена онтологія може бути корисна для спе­цифікації, поповнення і підтримки словників ПО, але онто­логічні словники мають обмежене використання, оскільки не вводять експліцитно значення термінів. Хоча в деяких випад­ках, коли використовувані терміни належать до дуже вузько­го (наприклад, технічного) словника, і їх значення вже напе­ред добре узгоджені в межах певного (наприклад, наукового) об’єднання, такі онтології застосовуються на практиці. Відо­мими прикладами онтології цього типу є індекси машин пошу­ку інформації в мережі Інтернет.

Інша ситуація у разі використання термінів природної мо­ви або в тих випадках, коли спілкуються програмні аґенти. У цьому випадку необхідно характеризувати передбачуване значення елементів словника за допомогою відповідної аксіоматизації, мета використання якої — вилучення небажа­них моделей і в тому, щоб інтерпретація була єдиною для всіх учасників спілкування.

Інший варіант відповідає випадку R=Ø, але F≠Ø. Тоді кожному елементу множини термінів із С може ставитися у відповідність функція інтерпретації f з F. Формально це твердження може записуватися таким чином.

Нехай С = С₁ С₂, причому С₁ С₂ = Ø, де С₁ — множина термінів, що інтерпретуються; С₂ — множина інтерпретаційних термінів.

Тоді

(с С₁, у¹, у², ....., у С₂),

такі що

с = f ( y¹, y²,…, y ),

де f є F.

Те, що перетин множин С₁ і С₂ — порожня множина виключає циклічні інтерпретації, а введення на розгляд функції k арґументів покликано забезпечити повнішу інтерпретацію. Тип відображення f із F визначає виразну потужність і практичну корисність цього виду онтології. Так, якщо припустити, що функція інтерпретації задається оператором присвоєння значень (С₁ : = С₂, де С₁ — ім’я інтерпретації С₂), то онтологія трансформується в пасивний словник V^р:

О = V^р = <С₁ С₂, {},{:=}>.

Такий словник пасивний, оскільки всі визначення термінів із С₁ беруться із вже наявної та фіксованої множини С₂. Практична цінність його вища, ніж простого словника, але недостатня, наприклад, для відображення знань у задачах опрацювання інформації в Інтернеті через динамічний харак­тер цього середовища.

Щоб врахувати останню обставину, припустимо, що части­на інтерпретаційних термінів із множини С₂ задається проце­дурно, а не декларативно. Значення таких термінів «обчис­люється» кожного разу при їх інтерпретації.

Цінність такого словника для задач опрацювання інфор­мації в середовищі Інтернет вища, ніж у попередньої моделі, але все ще недостатня, оскільки елементи, що інтерпретують­ся із С₁, ніяк не зв’язані між собою, отже, виконують лише роль ключів входження в онтологію.

Для відображення моделі онтології, яка потрібна для роз­в’язування задач опрацювання інформації в Інтернеті, очевид­но, вимагається відмовитися від припущення R = Ø.

Отже, припустимо, що множина відношень на концептах онтології не порожня, і розглянемо можливі варіанти її фор­мування.

Для цього введемо в розгляд спеціальний підклас онто­логії — просту таксономію, а отже:

О = Т⁰ = < С, {IS-A}, {} >.

Під таксономічною структурою будемо розуміти ієрар­хічну систему понять, зв’язаних між собою відношенням IS-A («бути елементом класу»).

Відношення IS-A має фіксовану наперед семантику і дозво­ляє організувати структуру понять онтології у вигляді дерева. Такий підхід має свої переваги і недоліки, але загалом є адек­ватним і зручним способом для відображення ієрархії понять.

Результати аналізу окремих випадків моделі онтології на­ведені в табл. 6.1.

Табл. 6.1. Класифікація моделей онтології.

Компоненти моделі	R = Ø F =Ø	R= Ø F ≠ Ø	R = Ø F ≠ Ø	R={IS-A} F = Ø
Формальне визначення	<С,{},{}>	<С1 С2 {},F>	<Сı (С2΄ ρ2΄), {}, F >	<С,{IS-A}, {}>
Пояснення	Словник ПО	Пасивний словник ПО	Активний словник ПО	Таксономія понять ПО

Далі можна узагальнити окремі випадки моделі онтології таким чином, щоб забезпечити можливість:

• відображення множини концептів С у вигляді мережевої структури;

• використання достатньо великої множини відношень, яка включає не тільки таксономічні відношення, але і відношення, що відображають специфіку конкретної предметної області, а також засоби розширення множини R;

• використання декларативних і процедурних інтерпре­тацій і відношень, включаючи можливість визначення нових інтерпретацій.

Тоді можна ввести в розгляд модель розширюваної онто­логії і досліджувати її властивості. Проте, враховуючи тех­нічну спрямованість цього підручника, ми не будемо робити цього тут, а охочих познайомитися з такою моделлю скеруємо до роботи [44]. Як показано в цій роботі, модель розширюваної онтології є досить могутньою для специфікації процесів фор­мування просторів знань в середовищі Інтернет. Разом з тим, і ця модель є неповною через свою пасивність навіть там, де визначені відповідні процедурні інтерпретації та введені спеціальні функції поповнення онтології. Адже єдиною точкою керування активністю в такій моделі є запит на інтер­претацію певного концепту. Цей запит виконується завжди однаково й ініціює запускання відповідної процедури. А влас­не виведення відповіді на запит чи пошук необхідної для цьо­го інформації залишається поза моделлю і повинен реалізову­ватися іншими засобами.

Враховуючи вищесказане, а також необхідність експліцитної специфікації процесів функціонування онтології, введемо в розгляд поняття онтологічної системи.

Під формальною моделлю онтологічної системи розуміють триплет вигляду:

= < O , {O }, Ξ >,

де O — онтологія верхнього рівня (метаонтологія); {О } — множина предметних онтологій і онтологій задач предметної області; Ξ — модель машини виведення, асоційованої з онтологічною системою .

Використання системи онтологій і спеціальної машини виведення дозволяє розв’язувати в такій моделі різні задачі. Збагачуючи систему моделей {О }, можна враховувати побажання користувача, а змінюючи модель машини виведення, вводити спеціалізовані критерії релевантності, що одержуються в процесі пошуку інформації, і формувати спеціальні репозиторії накопичених даних, а також поповнювати, при необхідності, використовувані онтології.

У моделі є три онтологічні компоненти: метаонтологія; предметна онтологія; онтологія задач.

Як показувалося вище, метаонтологія оперує загальними концептами і відношеннями, які не залежать від конкретної предметної області. Концептами метарівня є загальні поняття, такі як «об’єкт», «властивість», «значення» тощо. Тоді на рівні метаонтології ми отримуємо інтенсіональний опис влас­тивостей предметної онтології й онтології задач. Онтологія метарівня є статичною, що дає можливість забезпечити тут ефективне виведення.

Предметна онтологія O містить поняття, що описують конкретну предметну область, відношення, семантично зна­чущі для заданої предметної області, і множину інтерпретацій цих понять і відношень (декларативних і процедурних). По­няття предметної області специфічні в кожній прикладній он­тології, але відношення — універсальніші. Тому як базис зазвичай виділяють такі відношення моделі предметної онто­логії, як part_of, kind_of, contained_in, member_of, see_also і деякі інші.

Відношення part_of визначене на множині концептів, є відношенням належності і показує, що концепт може бути частиною інших концептів. Воно є відношенням виду «частина-ціле» і за властивостями близьке до відношення IS-A і може бути задане відповідними аксіомами. Аналогічним чином можна ввести й інші відношення виду «частина-ціле».

Відношення see_also має іншу семантику й інші властивості. Тому доцільно вводити його не декларативно, а процедурно, подібно до того, як це робиться при визначенні нових типів у мовах програмування, де підтримуються абстрактні типи даних:

X see_also Y:

see_also member_of Relation {

if ((X is_a Notion) & (Y is_a Notion) & (X see_also Y)) if (Operation connected_with X) Operation connected_with Y}.

Зазначимо, що і відношення see_also «не цілком» транзи­тивне. Так, якщо припустити, що (X1 see_also Х2) & (Х2 see_also X3), то можна вважати, що (X1 see_also Х3). Проте у міру збільшення довжини ланцюжка об’єктів, зв’язаних ци­ми відношеннями, справедливість транзитивного перенесення властивості connected_with зменшується. Тому у разі відно­шення see_also ми маємо справу не з відношенням часткового порядку (як, наприклад, у разі відношення IS-A), а з відношен­ням толерантності. Однак для простоти це обмеження може бути перенесене з визначення відношення у функцію його інтерпретації.

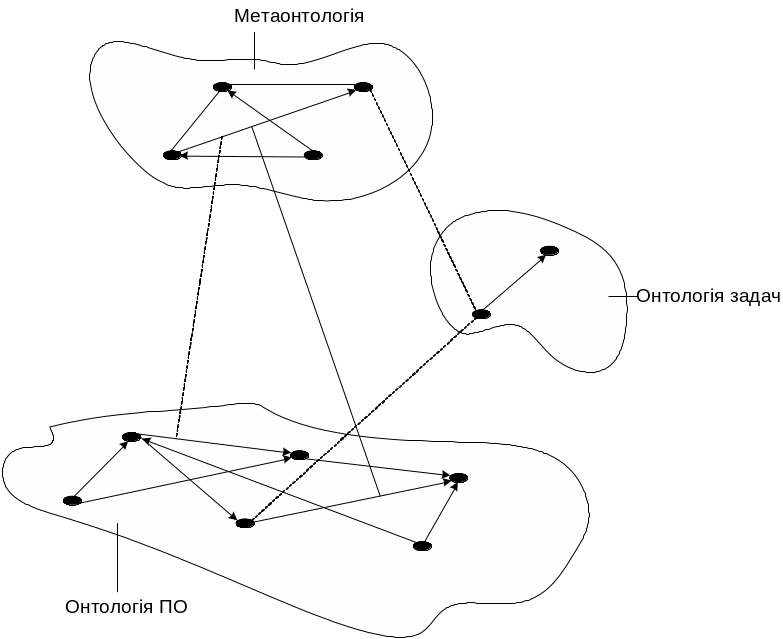
Рис. 6.4. Взаємозв’язок між онтологіями онтологічної системи.

Аналіз різних предметних областей показує, що введений вище набір відношень є достатнім для початкового опису відповідних онтологій. Зрозуміло, що цей базис є відкритим і може поповнюватися залежно від предметної області і цілей, що стоять перед прикладною системою, в якій така онтологія використовується.

Онтологія задач як поняття містить типи розв’язуваних задач, а відношення цієї онтології, як правило, специфікують декомпозицію задач на підзадачі. Разом з тим, якщо приклад­ною системою розв’язується єдиний тип задач (наприклад, за­дачі пошуку релевантного запиту інформації), то онтологія задач може в такому випадку описуватися словниковою моделлю, розглянутою вище. Отже, модель онтологічної сис­теми дозволяє описувати необхідні для її функціонування он­тології різних рівнів. Взаємозв’язок між онтологіями показаний на рис. 6.4.

Машина виведення онтологічної системи в загальному ви­падку може спиратися на мережеве відображення онтології всіх рівнів. При цьому її функціонування буде пов’язане:

• з активацією понять чи відношень, що фіксують задачу, яка розв’язується (опис первинної ситуації);

• визначенням цільового стану (ситуації);

• виведенням на мережі; полягає у тому, що від вузлів пер­винної ситуації розповсюджуються хвилі активації, що вико­ристовують властивості відношень, пов’язаних з ними. Кри­терієм зупинки процесу є досягнення цільової ситуації або перевищення тривалості виконання (time-out).