
- •4. Дифференцирование векторного поля.
- •6. Теоремы Грина.
- •12. Цилиндрическая система координат.
- •Цикл II. Физическое поле.
- •1. Скалярный потенциал безвихревого поля.
- •6. Классификация полей.
- •1. Изображение скалярного поля .
- •2. Графическое изображение векторного поля .
- •4. Вихревое поле в графическом изображении.
- •2. Поле дипольного источника.
4. Вихревое поле в графическом изображении.
 Пусть
есть поле
,
удовлетворяющее условиям
,
т.е поле
– поле вихрей. Так как это поле вихревое,
то
Пусть
есть поле
,
удовлетворяющее условиям
,
т.е поле
– поле вихрей. Так как это поле вихревое,
то
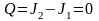 ,
и J2
= J1
справедливо для любых сечений. Это
означает, что векторные трубки и векторные
линии у такого поля всегда замкнуты.
Вихревое поле делит пространство на
замкнутые векторные трубки. Поэтому
вихревое поле называют трубчатым
полем (соленоидальным полем).
,
и J2
= J1
справедливо для любых сечений. Это
означает, что векторные трубки и векторные
линии у такого поля всегда замкнуты.
Вихревое поле делит пространство на
замкнутые векторные трубки. Поэтому
вихревое поле называют трубчатым
полем (соленоидальным полем).
 Рассмотрим
поле
.
Так как
Рассмотрим
поле
.
Так как
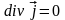 ,
то
- вихрь, и его вихревая трубка также
замкнута. Возможно две ситуации: вихревые
трубки полей
и
замкнуты вне друг друга или сцеплены
друг с другом. Для выяснения этой ситуации
рассмотрим циркуляцию вектора
вдоль
замкнутой силовой линии:
,
то
- вихрь, и его вихревая трубка также
замкнута. Возможно две ситуации: вихревые
трубки полей
и
замкнуты вне друг друга или сцеплены
друг с другом. Для выяснения этой ситуации
рассмотрим циркуляцию вектора
вдоль
замкнутой силовой линии:
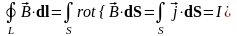 ,
т.е. она равна полному вихрю. Полный
вихрь отличен от нуля в случае, когда
и
сцеплены друг с другом.
,
т.е. она равна полному вихрю. Полный
вихрь отличен от нуля в случае, когда
и
сцеплены друг с другом.
Лекция X. Модели безвихревого поля (модели источников безвихревого поля).
Все сложные явления природы хочется описать математически. При этом описание должно быть достаточно близко к наблюдаемым явлениям. Условие близости определяет сам исследователь. Модели должны удовлетворять двум условиям: 1) близостью к природе, 2) достаточной простотой. Все модели можно разделить на два класса – физически осуществимые и физически не осуществимые.
1. Точечный источник.
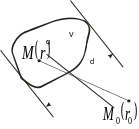 Представим
себе объем V, заполненный
источником с плотностью q.
Если плотность источника q
постоянна (q = const),
то говорят об однородном источнике,
если же плотность не постоянна (q
≠ const), то говорят
о неоднородном источнике. Полная масса
источника, сосредоточенная в объеме V,
равна
Представим
себе объем V, заполненный
источником с плотностью q.
Если плотность источника q
постоянна (q = const),
то говорят об однородном источнике,
если же плотность не постоянна (q
≠ const), то говорят
о неоднородном источнике. Полная масса
источника, сосредоточенная в объеме V,
равна
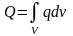 .
Потенциал u и поле
,
создаваемые таким источником, описывается
следующими соотношениями:
.
Потенциал u и поле
,
создаваемые таким источником, описывается
следующими соотношениями:
, .
Если
d – максимальный
диаметр объема V, и
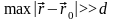 ,
т.е. точка наблюдения M0
находится на большом удалении от
источника, то расстояние
,
т.е. точка наблюдения M0
находится на большом удалении от
источника, то расстояние
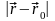 практически не меняется при перемещении
точки интегрирования M
внутри объема V. Тогда
для потенциала, создаваемого этим
источником, можно записать:
практически не меняется при перемещении
точки интегрирования M
внутри объема V. Тогда
для потенциала, создаваемого этим
источником, можно записать:
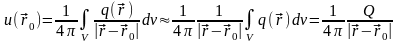 .
.
Полученное
выражение будет описывать потенциал
источника, стянутого в точку, т.е.
потенциал точечного источника. При этом
масса точечного источника остается
равной массе Q, а
плотность такого источника возрастает
до бесконечности. С помощью трехмерной
функции Дирихле для плотности точечного
источника можно записать
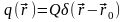 .
С учетом того, что
.
С учетом того, что
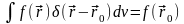 ,
можем записать:
,
можем записать:
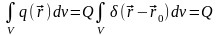 ,
и
,
и
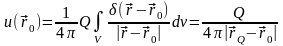 .
.
Поместив
точку
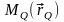 в начало координат, получим:
в начало координат, получим:
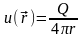 ,
, 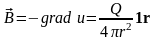 . (10.1)
. (10.1)
П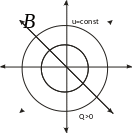 олученное
поле носит название центрального, т.к.
оно сферически симметрично.
олученное
поле носит название центрального, т.к.
оно сферически симметрично.
В
лекции VIII была введена
функция Грина
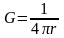 .
Из полученных результатов следует, что
функция Грина для решения уравнения
Пуассона – потенциал точечного источника
с единичной массой. Полученные выражения
для поля
описываются законами Кулона (1784 г.) и
Ньютона.
.
Из полученных результатов следует, что
функция Грина для решения уравнения
Пуассона – потенциал точечного источника
с единичной массой. Полученные выражения
для поля
описываются законами Кулона (1784 г.) и
Ньютона.
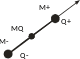
2. Поле дипольного источника.
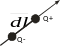

 Пусть
есть два ограниченных объема, заполненных
источниками таким образом, что массы
объемов равны, но противоположены по
знаку. Обозначим через D
максимальное расстояние между этими
объемами, координату точки, принадлежащей
одному из объемов через М, и координату
точки наблюдения через М0.
Тогда, если
Пусть
есть два ограниченных объема, заполненных
источниками таким образом, что массы
объемов равны, но противоположены по
знаку. Обозначим через D
максимальное расстояние между этими
объемами, координату точки, принадлежащей
одному из объемов через М, и координату
точки наблюдения через М0.
Тогда, если
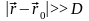 ,
то эти два источника можно моделировать
точечными с расстояниями между ними
равным Δl. Если
выполняется и условие
,
то эти два источника можно моделировать
точечными с расстояниями между ними
равным Δl. Если
выполняется и условие
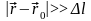 ,
то получим модель двойного точечного
источника или диполя. Точки, содержащие
точечные источники, – полюса диполя.
Линия, проходящая через полюса диполя,
носит название оси диполя. Ось имеет
ориентацию и направлена от отрицательной
массы (заряда) к положительной. Направление
оси диполя определяет поляризацию
диполя
,
то получим модель двойного точечного
источника или диполя. Точки, содержащие
точечные источники, – полюса диполя.
Линия, проходящая через полюса диполя,
носит название оси диполя. Ось имеет
ориентацию и направлена от отрицательной
массы (заряда) к положительной. Направление
оси диполя определяет поляризацию
диполя
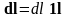 .
Массы (заряды) точечных источников в
диполе равны по величине, но противоположены
по знаку (|Q+| =
|Q-| = Q).
В этом случае суммарный заряд такой
конструкции будет равен нулю, и такая
система называется нейтральной.
Плоскость, проходящая через ось диполя,
называется меридианной плоскостью, а
ортогональная ей плоскость, проходящая
через центр диполя, носит название
экваториальной плоскости диполя.
Основной характеристикой диполя является
его момент
.
Массы (заряды) точечных источников в
диполе равны по величине, но противоположены
по знаку (|Q+| =
|Q-| = Q).
В этом случае суммарный заряд такой
конструкции будет равен нулю, и такая
система называется нейтральной.
Плоскость, проходящая через ось диполя,
называется меридианной плоскостью, а
ортогональная ей плоскость, проходящая
через центр диполя, носит название
экваториальной плоскости диполя.
Основной характеристикой диполя является
его момент
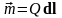 .
.
 Пусть
задан диполь с моментом
Пусть
задан диполь с моментом
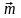 и
с центром в точке MQ.
Тогда потенциал диполя можем представить
как сумму потенциалов двух точечных
источников:
и
с центром в точке MQ.
Тогда потенциал диполя можем представить
как сумму потенциалов двух точечных
источников:
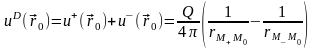 .
.
С учетом того, что для дифференциала скалярного поля a справедливо соотношение , можем записать:
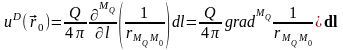 =
=
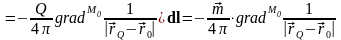 .
.
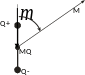
Поместив точку МQ в начало координат, получим:
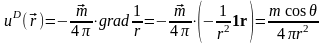 ,
,
где угол θ – угол между осью диполя и радиус-вектором, направленным из цента диполя в точку наблюдения М0. Поле в сферической системе координат будет иметь следующее представление:
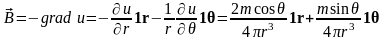 .
.
О кончательные
формулы:
кончательные
формулы:
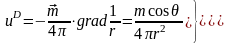 (10.2)
(10.2)
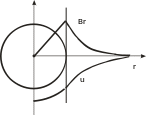
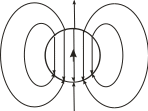
Поведение поля и потенциала точечного источника иллюстрируется рисунком. Поле диполя цилиндрически симметрично относительно оси диполя.
Замечание 1. Связь потенциалов точечного и дипольного источников описывается формулой Пуассона
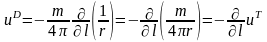 . (10.3)
. (10.3)
Замечание 2. Возможны и более сложные по сравнению с дипольной конструкцией расположения зарядов – квадруполи, октуполи и т.д., т.е. существует мультидипольный ряд. Так, например, квадруполь – четыре заряда, октуполь – 8 зарядов и т.д.
3. Линейный источник.
 Представим
себе нить, на которой с плотностью q
распределены источники. Выделим некоторый
элемент нити длинной Δl.
Тогда масса источника, сосредоточенная
в этом элементе будет равна ΔQ
= q·ΔS·Δl,
где ΔS – площадь
поперечного сечения нити. Отношение
Представим
себе нить, на которой с плотностью q
распределены источники. Выделим некоторый
элемент нити длинной Δl.
Тогда масса источника, сосредоточенная
в этом элементе будет равна ΔQ
= q·ΔS·Δl,
где ΔS – площадь
поперечного сечения нити. Отношение
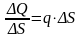 характеризует плотность распределения
источников вдоль нити. Такую плотность
называют линейной плотностью. Если
расстояние от точки наблюдения до
элемента нити Δl
много больше диаметра нити, то в этом
случае поле практически не изменится,
если сжать эту нить (ΔS
→ 0), а плотность q
устремить к бесконечности, но так, чтобы
сохранилось условие
характеризует плотность распределения
источников вдоль нити. Такую плотность
называют линейной плотностью. Если
расстояние от точки наблюдения до
элемента нити Δl
много больше диаметра нити, то в этом
случае поле практически не изменится,
если сжать эту нить (ΔS
→ 0), а плотность q
устремить к бесконечности, но так, чтобы
сохранилось условие
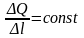 .
В результате таких действий мы получили
нить, нагруженную источниками с линейной
плотностью
.
В результате таких действий мы получили
нить, нагруженную источниками с линейной
плотностью
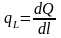 .
Такую модель можно рассматривать и как
линию, нагруженную точечными источниками
с массой
.
Такую модель можно рассматривать и как
линию, нагруженную точечными источниками
с массой
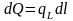 .
Полная масса источника, на линии L
равна
.
Полная масса источника, на линии L
равна
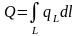 .
.
Потенциал линейного источника и поле, создаваемое им, описываются следующими соотношениями:
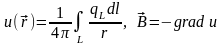 . (10.4)
. (10.4)
Рассмотрим поля, создаваемые моделями линейных источников.
Модель 1. Прямолинейный однородный источник конечной длины (стержень).
Линейная плотность такого источника постоянна и равна qL. Длину источника положим равной 2l. При выводе выражений для потенциала и поля будем использовать цилиндрическую систему координат, в которой ось Z совпадает со стержнем, а начало координат находится на середине стержня. Тогда
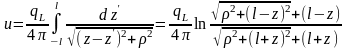 ,
,
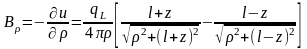 ,
,
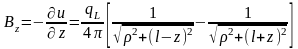 ,
,
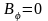 .
.
Х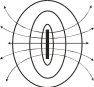 арактер
поведения векторных линий и эквипотенциальных
поверхностей показан на рисунке. При
увеличении расстояния точки наблюдения
до источника поле такой модели будет
приближаться к полю точечного источника.
арактер
поведения векторных линий и эквипотенциальных
поверхностей показан на рисунке. При
увеличении расстояния точки наблюдения
до источника поле такой модели будет
приближаться к полю точечного источника.
Модель 2. Бесконечно длинный однородный прямолинейный источник. Логарифмический потенциал.
Проанализируем характер поведения потенциала и поля стержня при l→∞:
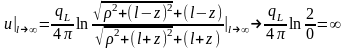 ,
,
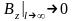 ,
,
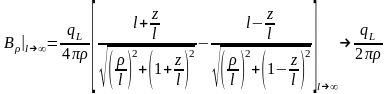 ,
,
т.е.
существует асимптотические равенства
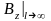
0,
0,
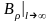
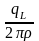 .
.
Таким образом, нами получена модель, в которой потенциал поля равен бесконечности, но само поле, создаваемое такой моделью существует и ограничено. Такая модель физически невозможна, поскольку для ее построения необходима бесконечная энергия.
Вернемся к выражению для потенциала этой модели:
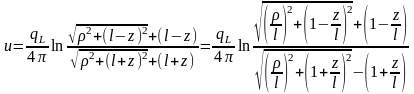 .
.
Положив
z = 0 и воспользовавшись
разложением в ряд Тейлора квадратного
корня
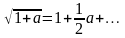 ,
осуществим дальнейшие преобразования:
,
осуществим дальнейшие преобразования:
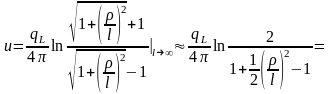
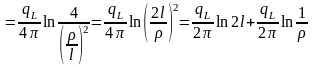 .
.
Выражение для потенциала распалось на два слагаемых. Первое слагаемое растет с увеличением длины источника и не зависит от положения точки наблюдения. Это слагаемое можно отбросить из рассмотрения, поскольку оно будет постоянной для всех точек наблюдения. В результате выражение для потенциала и поля приобретают вид:
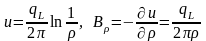 .
.
 Потенциал
бесконечного источника носит название
логарифмического. Этот потенциал имеет
две особенности – в бесконечности и на
самом источнике. Эквипотенциальные
поверхности представляют собой цилиндры,
векторные линии – лучи, выходящие из
источника. Потенциал u
и поле
не зависят от координаты z.
Такие поля, которые зависят от двух
координат, называются двумерными.
Потенциал
бесконечного источника носит название
логарифмического. Этот потенциал имеет
две особенности – в бесконечности и на
самом источнике. Эквипотенциальные
поверхности представляют собой цилиндры,
векторные линии – лучи, выходящие из
источника. Потенциал u
и поле
не зависят от координаты z.
Такие поля, которые зависят от двух
координат, называются двумерными.
Модель 3. Однородный круговой цилиндр.
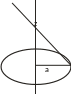 Источник
в виде круга радиуса R
= a с плотностью qL
= const. В общем случае задача
сводится к эллиптическим интегралам,
которые не берутся в явном виде, либо к
разложению по полиномам Лежандра.
Источник
в виде круга радиуса R
= a с плотностью qL
= const. В общем случае задача
сводится к эллиптическим интегралам,
которые не берутся в явном виде, либо к
разложению по полиномам Лежандра.
Рассмотрим частный случай, когда точка наблюдения находится на оси Z:
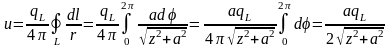 ,
,
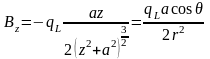 .
.
Поведение
потенциала и поля при прохождении через
плоскость кольца иллюстрируется
графиками. Потенциал максимален при z
= 0, т.е. в центре плоскости кольца, и равен
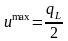 ,
значение поля в этой точке равно нулю.
Максимальных значений поле достигает
при
,
значение поля в этой точке равно нулю.
Максимальных значений поле достигает
при
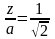 и равно
и равно
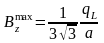 .
.
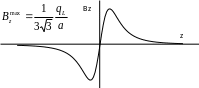
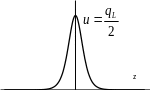
4. Поверхностный источник (простой слой).
 Представим
себе слой толщиной Δh,
содержащий источники с объемной
плотностью q. Выделим
малый элемент ΔV,
плотность в котором можно считать
постоянной. Масса источника, содержащаяся
в этом объеме, будут равна ΔQ
= qΔhΔS.
Ведем величину
Представим
себе слой толщиной Δh,
содержащий источники с объемной
плотностью q. Выделим
малый элемент ΔV,
плотность в котором можно считать
постоянной. Масса источника, содержащаяся
в этом объеме, будут равна ΔQ
= qΔhΔS.
Ведем величину
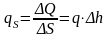 .
Представим, что мы стягиваем поверхности
слоя друг к другу. Тем самым расстояние
Δh будет стремиться
к нулю, плотность слоя q
будет увеличиваться, но общая масса
источников должна остаться без изменений,
и без изменения должна остаться величина
.
Представим, что мы стягиваем поверхности
слоя друг к другу. Тем самым расстояние
Δh будет стремиться
к нулю, плотность слоя q
будет увеличиваться, но общая масса
источников должна остаться без изменений,
и без изменения должна остаться величина
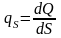 ,
которая носит название поверхностной
плотности зарядов. Тем самым нами
построена модель поверхностного
источника с плотностью зарядов qS.
Поверхностный источник можно представить
себе как поверхность, нагруженную
точечными источниками. Элемент площади
поверхности содержит массу источников
,
которая носит название поверхностной
плотности зарядов. Тем самым нами
построена модель поверхностного
источника с плотностью зарядов qS.
Поверхностный источник можно представить
себе как поверхность, нагруженную
точечными источниками. Элемент площади
поверхности содержит массу источников
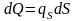 .
Полный заряд, распределенный на
поверхности, определяется интегралом
.
Полный заряд, распределенный на
поверхности, определяется интегралом
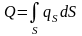 .
Выражения для потенциала и поля будут
иметь вид:
.
Выражения для потенциала и поля будут
иметь вид:
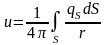 ,
.
,
.
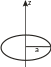
Пример 1. Круговой диск с постоянной плотностью qS = const.
Обозначим радиус диска буквой a, и введем цилиндрическую систему координат с осью Z, совпадающей с осью диска. Будем рассматривать поле на оси Z:
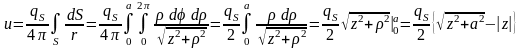 .
.
Перепишем это соотношение более наглядно:
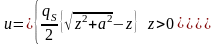 ,
,
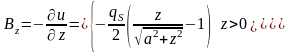 .
.
На больших расстояниях от источника (|z|>>a) поле диска приближается к полю точечного источника:
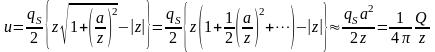 ,
,
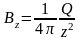 .
.
На малых расстояниях (|z|<<a):
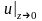
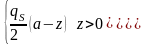 ;
;
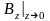
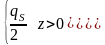 .
.
На поверхности диска:
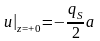 ,
, 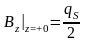
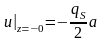 ,
, 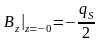 .
.
Полученный результат показывает, что потенциал, создаваемое диском, непрерывен, а поле, на самом диске терпит разрыв:
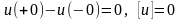 ;
;
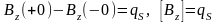 .
.
Пример 2. Бесконечная плоскость с постоянной поверхностной плотностью (qS = const).
В модели диска устремим радиус a к бесконечности (a → ∞). В этом случае, при любом конечном z выполняется условие |z|<< a:
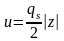 ,
, 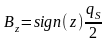 .
.
Бесконечная плоскость делит пространство на две зеркально симметричных части, в которых потенциал линейно растет с увеличением |z|, а поле нормально направлено к плоскости и постоянно (поле однородно в верхнем и нижнем полупространствах). Так как поле постоянно, то и . Это означает, что поле не имеет источников и вихрей. Полученное таким образом поле – абстракция, как и поле бесконечно длинного линейного источника, но оно удобно при решении ряда геофизических задач, когда рассматриваются поля плоских источников на небольших удалениях от самих источников.
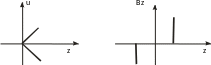
Граничные условия на поверхностном источнике.


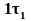
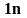
 Вырежем
на поверхностном источнике элемент ΔS.
Потенциал будет складываться из значений
потенциала элемента ΔS
и потенциала, создаваемого поверхностным
источником без элемента ΔS:
Вырежем
на поверхностном источнике элемент ΔS.
Потенциал будет складываться из значений
потенциала элемента ΔS
и потенциала, создаваемого поверхностным
источником без элемента ΔS:
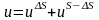 .
Как нами уже было показано для случая
кругового источника
.
Как нами уже было показано для случая
кругового источника
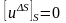 .
В то же время, потенциал
.
В то же время, потенциал
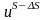 в точке, находящейся на площади ΔS,
также не терпит разрыва, поскольку эта
точка не принадлежит источнику:
в точке, находящейся на площади ΔS,
также не терпит разрыва, поскольку эта
точка не принадлежит источнику:
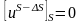 .
Следовательно, потенциал всего
поверхностного источника неразрывен:
.
Следовательно, потенциал всего
поверхностного источника неразрывен:
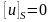 .
.
Так как потенциал непрерывен вдоль всей поверхности, то для тангенциальных компонент поля можно написать:
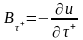 ,
, 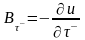 ,
,
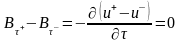 или
или
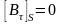 .
.
Тангенциальные компоненты поля на источнике непрерывны.
Нормальная
компонента поля для элемента ΔS
терпит разрыв
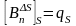 .
Компонента Bn
для плоскости [S- ΔS]
непрерывна, т.е.
.
Компонента Bn
для плоскости [S- ΔS]
непрерывна, т.е.
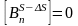 .
Следовательно,
.
Следовательно,
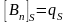 .
.
Таким образом, граничные условия для поверхностного источника имеют вид:
, , . (10.6)
5. Двойной поверхностный источник (двойной слой, дипольный слой).
 Модель
такого источника можно рассматривать
в виде двух простых слоев с противоположенными
знаками, находящихся рядом друг с другом.
Если точка наблюдения расположена на
большом расстоянии от источника, то
модель будет представлять собой два
простых слоя бесконечно близко
расположенных друг к другу и с
поверхностными плотностями +qS
и –qS.
Такую модель можно рассматривать, как
поверхность, нагруженную дипольными
источниками. Элемент площади
такой поверхности будет иметь магнитный
момент
Модель
такого источника можно рассматривать
в виде двух простых слоев с противоположенными
знаками, находящихся рядом друг с другом.
Если точка наблюдения расположена на
большом расстоянии от источника, то
модель будет представлять собой два
простых слоя бесконечно близко
расположенных друг к другу и с
поверхностными плотностями +qS
и –qS.
Такую модель можно рассматривать, как
поверхность, нагруженную дипольными
источниками. Элемент площади
такой поверхности будет иметь магнитный
момент
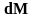 .
Тогда плотность дипольных источников,
распределенных по поверхности, будет
равна
.
Тогда плотность дипольных источников,
распределенных по поверхности, будет
равна
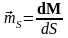 .
Такой источник носит название дипольного
(двойного) поверхностного источника
или двойного слоя. Суммарный момент
двойного слоя равен
.
Такой источник носит название дипольного
(двойного) поверхностного источника
или двойного слоя. Суммарный момент
двойного слоя равен
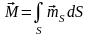 .
.
Потенциал, создаваемый элементарной площадкой в точке М0, не лежащей на двойном слое, может быть представлен выражением (10.2):
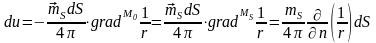 ,
,
а для потенциала всего слоя можно записать:
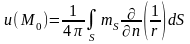 . (10.7)
. (10.7)
 Введем
понятие телесного угла. Телесный угол
– часть пространства, ограниченного
конической поверхностью. Величина
телесного угла определяется как отношение
площади сферической поверхности, видимой
из вершины конической поверхности, к
квадрату радиуса этой сферы:
Введем
понятие телесного угла. Телесный угол
– часть пространства, ограниченного
конической поверхностью. Величина
телесного угла определяется как отношение
площади сферической поверхности, видимой
из вершины конической поверхности, к
квадрату радиуса этой сферы:
dS
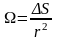
 .
.
Так, для всей сферы Ω = 4, а для полусферы Ω = 2. При произвольном расположении площадки , телесный угол будет определяться через отношение проекции площадки на сферическую поверхность, построенной из точки наблюдения, к квадрату радиуса этой сферы:
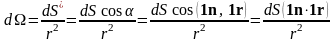 .
.
В частности, из этого соотношения следует, что телесный угол может иметь отрицательное значение.
Используя понятие телесного угла, выражение для потенциала двойного слоя можно представить в следующем виде:
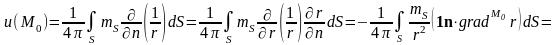
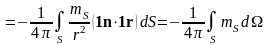 .
.
При
выводе этого выражения, мы воспользовались
представлением
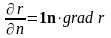 и перешли к дифференцированию от точки
интегрирования М по точке наблюдения
М0.
и перешли к дифференцированию от точки
интегрирования М по точке наблюдения
М0.
Таким образом, потенциал двойного слоя представляется выражением:
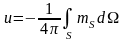 .
.
Для
однородного двойного слоя –
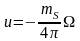 .
.
M2 ример
1. Замкнутая поверхность S,
нагруженная диполями. Для точки наблюдения
M1,
находящейся внутри объема, ограниченного
этой поверхностью, u(M1)
= mS.
Для точки M2,
расположенной вне объема, u(M2)
= 0. Поле
всюду равно нулю:
ример
1. Замкнутая поверхность S,
нагруженная диполями. Для точки наблюдения
M1,
находящейся внутри объема, ограниченного
этой поверхностью, u(M1)
= mS.
Для точки M2,
расположенной вне объема, u(M2)
= 0. Поле
всюду равно нулю:
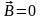 .
.
П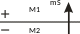 ример
2. Бесконечный плоский однородный
двойной слой:
ример
2. Бесконечный плоский однородный
двойной слой:
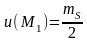 ,
,
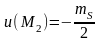 ,
.
,
.
П ример
3. Различные двойные слои с одинаковой
плотностью mS,
и опирающиеся на один и тот же контур
L, создают одинаковые
поля.
ример
3. Различные двойные слои с одинаковой
плотностью mS,
и опирающиеся на один и тот же контур
L, создают одинаковые
поля.
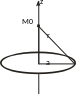
Пример
4. Двойной слой в виде диска с mS
= const. Будем рассматривать
поле на оси Z, проходящей
через центр диска. Тогда
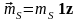 .
В точках, расположенных выше диска
(z>0),
.
В точках, расположенных выше диска
(z>0),
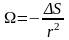 ,
где S
– площадь кругового сегмента (
,
где S
– площадь кругового сегмента (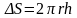 )
:
)
:
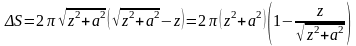 ,
,
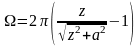 .
.
При z<0:
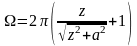 .
.
Можно написать общее выражение для телесного угла, которое будет учитывать положение точки наблюдения (выше или ниже диска):
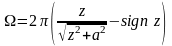 .
.
Соответствующее выражение для потенциала и поля:
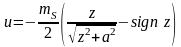 ,
,
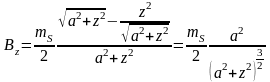 .
.
Граничные условия на поверхности диска:
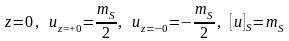 ,
,
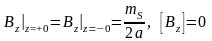 .
.
Условия на произвольном двойном слое.
 ,
,
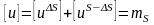 ,
,
(10.9)
 ,
,
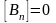 .
.
6. Объемные источники поля.
 Скалярный
потенциал и поле объемного источника:
Скалярный
потенциал и поле объемного источника:
q
V
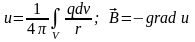 . (10.10)
. (10.10)
Пример 1. Поле однородной сферы.
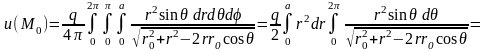

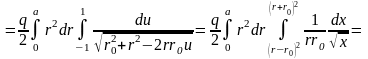
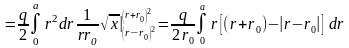 .
.
Окончательно:
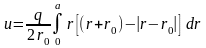 ,
,
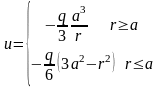 ,
,
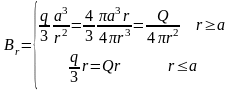 .
.
Вне
сферы поле сферического источника
совпадает с полем точечного источника
с массой Q и расположенного
в центре этой сферы. В центре сферы
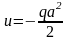 ,
.
Внутри сферы поле возрастает линейно.
Внешний сферический слой поля внутри
сферы не создает.
,
.
Внутри сферы поле возрастает линейно.
Внешний сферический слой поля внутри
сферы не создает.

Свойства
полей и потенциалов объемного источника:
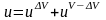 ,
,
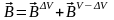 .
M0
– особая точка, т.к. в ней интеграл
несобственный. Требуется доказательство
сходимости. Потенциал u
и поле
внутри источника конечны и непрерывны:
.
M0
– особая точка, т.к. в ней интеграл
несобственный. Требуется доказательство
сходимости. Потенциал u
и поле
внутри источника конечны и непрерывны:
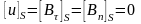 . (10.11)
. (10.11)
7. Поляризованный объемный источник.
V Объем
V, заполненный диполями
с непрерывно меняющимися моментами, –
поляризованный объемный источник.
Элемент dV имеет
элементарный момент
.
Тогда
Объем
V, заполненный диполями
с непрерывно меняющимися моментами, –
поляризованный объемный источник.
Элемент dV имеет
элементарный момент
.
Тогда
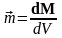 определяет плотность дипольных моментов
или поляризацию. Суммарный момент объема
V будет равен
определяет плотность дипольных моментов
или поляризацию. Суммарный момент объема
V будет равен
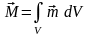 .
.
На
основании выражения для потенциала
диполя
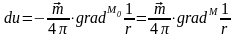 , напишем выражение для потенциала
объемного поляризованного источника:
, напишем выражение для потенциала
объемного поляризованного источника:
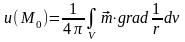 .
.
Используя
соотношение
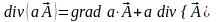 ,
преобразуем выражение для потенциала:
,
преобразуем выражение для потенциала:
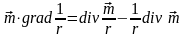 ,
,
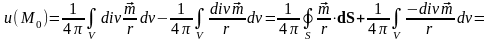
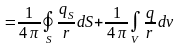 ,
,
Таким
образом, поле поляризованного источника
можно представить в виде суммы полей
объемного источника с плотностью зарядов
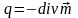 и поля простого слоя с поверхностной
плотностью зарядов
и поля простого слоя с поверхностной
плотностью зарядов
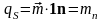 .
Этот факт имеет простое физическое
объяснение: часть зарядов внутри объема
компенсируются, а не скомпенсированные
заряды образуют поле. Кроме того,
возникают не скомпенсированные заряды
на поверхности объема, которые также
создают поле.
.
Этот факт имеет простое физическое
объяснение: часть зарядов внутри объема
компенсируются, а не скомпенсированные
заряды образуют поле. Кроме того,
возникают не скомпенсированные заряды
на поверхности объема, которые также
создают поле.
В
случае однородной поляризации
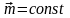 ,
и выражение для потенциала приобретает
вид:
,
и выражение для потенциала приобретает
вид:
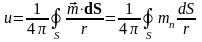 ,
,
т.е. поле объемного источника эквивалентно полю простого слоя, ограничивающего этот объем.
Граничные
условия на поляризованном источнике.
Можно представить потенциал объемного
поляризованного источника в виде суммы
потенциалов объемного источника и
поверхностного слоя:
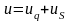 .
Потенциалы
.
Потенциалы
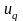 и
и
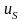 всюду непрерывны, следовательно
.
Поле
всюду непрерывны, следовательно
.
Поле
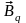 ,
создаваемое объемным источником,
непрерывно всюду, а для его поверхностных
компонент выполняются условия
,
создаваемое объемным источником,
непрерывно всюду, а для его поверхностных
компонент выполняются условия
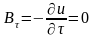 .
Для нормальной компоненты поля
поверхностного источника выполняется
условие
.
В нашем случае
.
Для нормальной компоненты поля
поверхностного источника выполняется
условие
.
В нашем случае
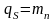 .
Окончательно можно записать:
.
Окончательно можно записать:
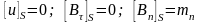 (10.13)
(10.13)
Формула Пуассона. Для однородно поляризованного источника:
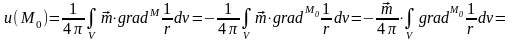
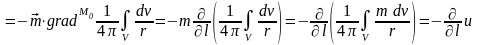 . (10.14),
. (10.14),
где - потенциал объемного источника с плотностью зарядов q = m.
О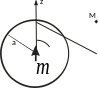 днородно
поляризованный сферический источник.
днородно
поляризованный сферический источник.
 .
Ось z совпадает с осью
поляризации. Воспользуемся формулой
Пуассона
.
Ось z совпадает с осью
поляризации. Воспользуемся формулой
Пуассона
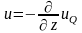 ,
где
,
где
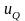 - потенциал однородной сферы с объемной
плотностью источников q
= m:
- потенциал однородной сферы с объемной
плотностью источников q
= m:
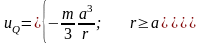 ,
,
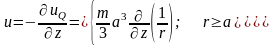 .
.
Воспользуемся представлением радиуса r с через угол :
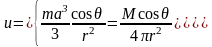 ,
,
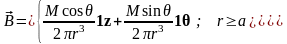
 Вне
сферы поле поляризованного источника
совпадает с полем диполя, расположенного
в центре сферы. Внутри сферы поле
однородно и антипараллельно
.
Вне
сферы поле поляризованного источника
совпадает с полем диполя, расположенного
в центре сферы. Внутри сферы поле
однородно и антипараллельно
.
Лекция XI. Модели вихревого поля (модели источников вихревого поля).
Предварительное
замечание. Существует поле
,
которое удовлетворяет условиям:
.
Из этих условий следует, что
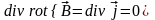 ,
т.е. поле
–
соленоидально во всем пространстве, а
это означает, что оно само не имеет
источников. Рассмотрим модели, создающие
вихревое поле.
,
т.е. поле
–
соленоидально во всем пространстве, а
это означает, что оно само не имеет
источников. Рассмотрим модели, создающие
вихревое поле.
1. Линейный вихрь.
S Представим
себе тонкую замкнутую трубку, содержащую
в себе вихревую линию, т.е. линию, которая
создает поле
.
Пусть
Представим
себе тонкую замкнутую трубку, содержащую
в себе вихревую линию, т.е. линию, которая
создает поле
.
Пусть
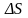 – сечение трубки. Вихревое поле
полностью находится в вихревой трубке.
Интенсивность трубки будет определяться
соотношением
– сечение трубки. Вихревое поле
полностью находится в вихревой трубке.
Интенсивность трубки будет определяться
соотношением
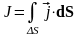 .
Пусть
уменьшается, т.е. трубка стягивается в
линию. При этом вектор
остается нормален к площадке
.
При стремлении
к нулю,
будет стремиться к бесконечности, но
при этом значение интенсивности трубки
J должно оставаться
постоянным (J =
const). Полученная таким
образом линия – линейный вихрь.
.
Пусть
уменьшается, т.е. трубка стягивается в
линию. При этом вектор
остается нормален к площадке
.
При стремлении
к нулю,
будет стремиться к бесконечности, но
при этом значение интенсивности трубки
J должно оставаться
постоянным (J =
const). Полученная таким
образом линия – линейный вихрь.
Векторный потенциал линейного вихря:
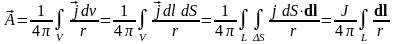 .
.
Для замкнутой линии:
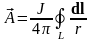 .
.
Потенциал и поле, создаваемые линейным вихрем будут описываться выражениями:
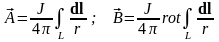 . (11.1)
. (11.1)
Рассмотрим
элемент линейного вихря
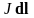 .
Поле, создаваемое этим элементом, будет
равно (при этом воспользуемся соотношением
.
Поле, создаваемое этим элементом, будет
равно (при этом воспользуемся соотношением
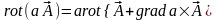 ):
):
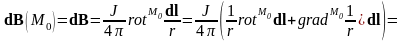
т.к.
элемент
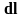 не зависит от положения точки M0,
то
не зависит от положения точки M0,
то
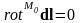 ,
и
,
и
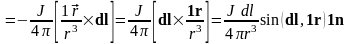 ,
(11.2)
,
(11.2)
при
этом элементы
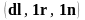 образуют правую тройку.
образуют правую тройку.
Поле линейного вихря:
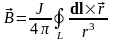 . (11.3)
. (11.3)
Выражение
для элемента поля
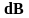 ,
,
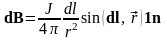 ,
,
носит название закона Био – Савара.
2. Эквивалентность линейного вихря однородному двойному слою.
Преобразуем выражение для потенциала линейного вихря:
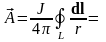 на
основании ф. Стокса =
на
основании ф. Стокса = .
.
Т.к. , то для дальнейших преобразований воспользуемся соотношениями:
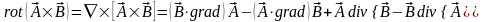 ,
,
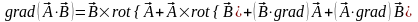 .
.
Обратим
внимание, что при
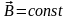 :
:
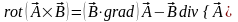 ,
,
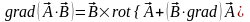 .
.
Тогда
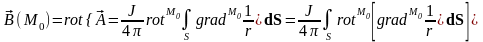 .
.
Рассмотрим подинтегральное выражение:
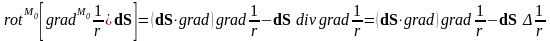 .
.
Так
как r ≠ 0, то
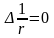 ,
и, следовательно,
,
и, следовательно,
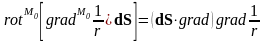 .
.
В то же время
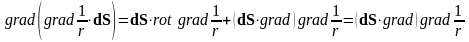 .
.
Таким образом, нами показано, что
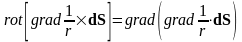 .
.
В результате выражение для поля можно преобразовать следующим образом:
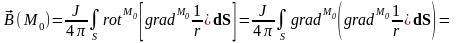
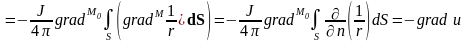 ,
,
где,
согласно формуле (10.7),
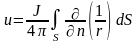 – потенциал однородного двойного слоя
с плотность m = J.
– потенциал однородного двойного слоя
с плотность m = J.
Результат:
Линейный вихрь L
интенсивностью J
создает такое же поле, как ограниченный
контуром L произвольный
двойной слой с плотностью
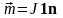 ,
при этом слой не проходит через точку
наблюдения. Скалярный потенциал линейного
вихря можно выразить через телесный
угол видимости:
,
при этом слой не проходит через точку
наблюдения. Скалярный потенциал линейного
вихря можно выразить через телесный
угол видимости:
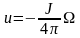 .
.
3. Различные выражения поля диполя.
Скалярный потенциал поля диполя имеет вид:
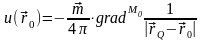 ,
,
или
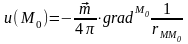 .
.
В этом случае поле , создаваемое диполем, определяется выражением
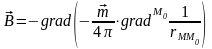 .
.
С учетом того, что момент диполя постоянен ( ), выражение для потенциала диполя можно представить следующим образом:
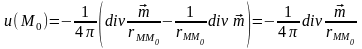 ,
,
и,
соответственно с учетом того, что
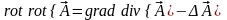 ,
для поля
можно записать:
,
для поля
можно записать:
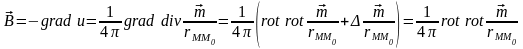 .
.
Лапласиан
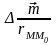 равен нулю (
равен нулю (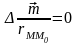 )
по той причине, что точка M0,
в которой определяется поле, не совпадает
с точкой M расположения
диполя. Отсюда следует, что поле диполя
может быть определено через векторный
потенциал, который имеет вид:
)
по той причине, что точка M0,
в которой определяется поле, не совпадает
с точкой M расположения
диполя. Отсюда следует, что поле диполя
может быть определено через векторный
потенциал, который имеет вид:
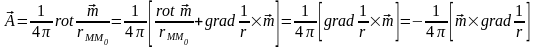 .
.
Таким образом, нами показано, что поле диполя может определяться как через скалярный, так и векторный потенциалы:
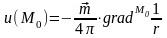 ,
,
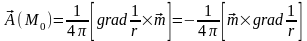 .
.
Соответственно и поле может быть определено через эти потенциалы:
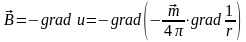 ,
,
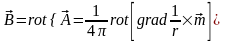 .
.
Пример 1. Круговой линейный вихрь радиусом a.
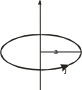 Скалярный
потенциал кругового линейного вихря
можно определить через телесный угол
видимости этого вихря. Тогда для точек,
расположенных на оси, проходящей через
центр вихря, справедливы следующие
соотношения:
Скалярный
потенциал кругового линейного вихря
можно определить через телесный угол
видимости этого вихря. Тогда для точек,
расположенных на оси, проходящей через
центр вихря, справедливы следующие
соотношения:
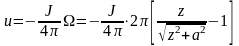 ,
при z > 0
,
при z > 0
и
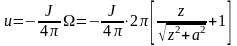 ,
при z < 0.
,
при z < 0.
На больших расстояниях точки наблюдения M0 от вихря, поле такого вихря будет приближаться к полю диполя. Так на пример, при z >> 0,
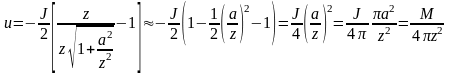 ,
,
где
 – дипольный момент кругового вихря.
– дипольный момент кругового вихря.
Пример 2. Бесконечно длинный прямолинейный вихрь.
J Линейный
вихрь интенсивностью J
замыкается в бесконечности. В этом
случае формально определяемый векторный
потенциал
будет представлен расходящимся
интегралом. Тем не менее, поле
такого вихря существует, и оно удовлетворяет
условиям:
Линейный
вихрь интенсивностью J
замыкается в бесконечности. В этом
случае формально определяемый векторный
потенциал
будет представлен расходящимся
интегралом. Тем не менее, поле
такого вихря существует, и оно удовлетворяет
условиям:
.
Выделим круговую площадку S, которую ортогонально будет пересекать линейный вихрь. Тогда для полного потока линейного вихря через эту площадку можно записать:
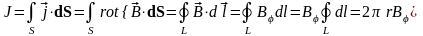 .
.
Таким
образом, поле бесконечно длинного
прямолинейного вихря будет равно
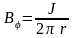 .
.
3. Поверхностный вихрь.
 Представим
себе замкнутый слой толщиной Δh,
содержащий вихри с объемной плотностью
и ограниченный поверхностями S1
и S2.
При уменьшении толщины слоя Δh
плотность вихря
будет возрастать, но так, что величина
Представим
себе замкнутый слой толщиной Δh,
содержащий вихри с объемной плотностью
и ограниченный поверхностями S1
и S2.
При уменьшении толщины слоя Δh
плотность вихря
будет возрастать, но так, что величина
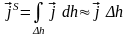 будет ограничена. Мы создали модель
поверхностного вихря. Если величина
будет ограничена. Мы создали модель
поверхностного вихря. Если величина
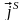 постоянна, то это будет модель однородного
поверхностного вихря.
постоянна, то это будет модель однородного
поверхностного вихря.
Отметим некоторые особенности поверхностного вихря.
1.
Нормальная компонента поверхностного
вихря равна нулю:
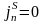 .
.
2.
Из условия соленоидальности вихря (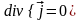 )
следует, что
)
следует, что
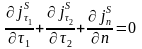 .
.
Отсюда вытекают условия, которым удовлетворяют тангенсиальные компоненты вихря:
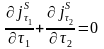 .
.
3. Векторный потенциал и поле поверхностного вихря определяются выражениями:
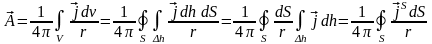 . (11.5)
. (11.5)
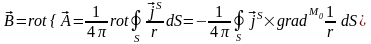 .
.
Последнее соотношение следует из того, что
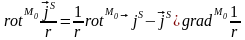 ,
,
при
этом учитывается тот факт, что
не зависит от точки наблюдения M0,
и, следовательно, слагаемое
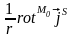 равно нулю.
равно нулю.
М одель
плоского поверхностного вихря.
одель
плоского поверхностного вихря.
h
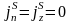 ,
,
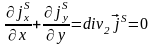 .
.
Введем
скалярную функцию
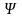 и
с ее помощью представим поверхностный
вихрь
в виде:
и
с ее помощью представим поверхностный
вихрь
в виде:
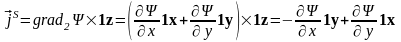 , (11.6)
, (11.6)
т.е.
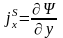 и
и
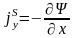 .
.
Выделим некоторую линию L, лежащую в плоскости вихря между точками M1 и M2, и рассчитаем поток вихря, проходящего через эту линию:
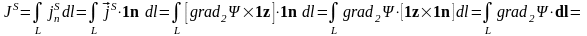
=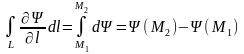 ,
,
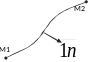
при этом орт нормали лежит в плоскости вихря. Мы получили соотношение, согласно которому поток вихря через линию L, определяется через значение функции . Функция получила название функции потока.
Напишем
уравнение для вихревой линии:
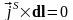 .
Тогда
.
Тогда
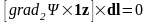 ,
или
,
или
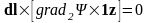 .
Дальнейшие преобразования будут
следующими:
.
Дальнейшие преобразования будут
следующими:
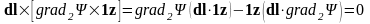 .
.
Поскольку
элемент
всегда
ортогонален орту
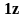 ,
то первое слагаемое будет равно нулю.
Для того чтобы написанное равенство
выполнялось, необходимо выполнение
условия
,
то первое слагаемое будет равно нулю.
Для того чтобы написанное равенство
выполнялось, необходимо выполнение
условия
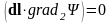 .
Это возможно в том случае, если функция
потока
будет
постоянной (
.
Это возможно в том случае, если функция
потока
будет
постоянной (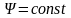 ).
Из этого следует, что векторные линии
плотности поверхностного вихря совпадают
с изолиниями функции потока.
).
Из этого следует, что векторные линии
плотности поверхностного вихря совпадают
с изолиниями функции потока.
Эти
выкладки можно обобщить на любую гладкую
поверхность и определить поверхностную
плотность вихря следующим соотношением:
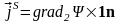 ,
где
– орт нормали к поверхностному вихрю,
,
где
– орт нормали к поверхностному вихрю,
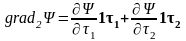 .
.
Векторный потенциал будет определяться следующим образом:
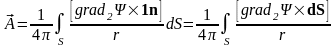 =
*
=
*
доопределим до замкнутой поверхности
*=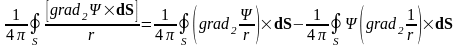 .
.
Так
как
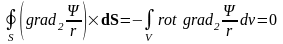 ,
то
,
то
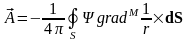 .
.
Соответственно, для поля можно записать:
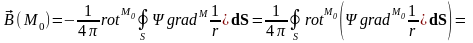
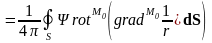 .
.
Воспользовавшись
соотношением (положив при этом
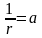 ):
):
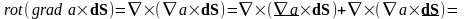
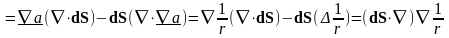 ,
,
окончательно получим
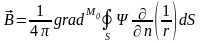 . (11.7)
. (11.7)
Полученный результат показывает, что поверхностный вихрь эквивалентен двойному слою с плотностью дипольных моментов, равной функции потока.
Граничные условия.
Проведем аналогию с двойным слоем:
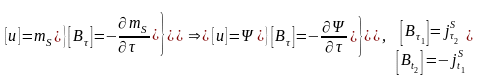 . (11.8)
. (11.8)
4. Объемный вихрь.
Рассмотрим некоторый объем, в котором содержаться вихри, и они замыкаются в этом объеме, т.е. не пересекают поверхность, ограничивающую этот объем. Тогда
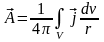 .
.
Так
как поле
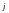 образует соленоидальное поле, т.е.
образует соленоидальное поле, т.е.
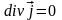 ,
то можно представить
,
то можно представить
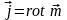 ,
где
– некоторый вектор. В этом случае:
,
где
– некоторый вектор. В этом случае:
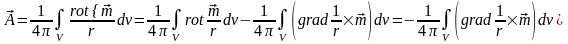 , (11.9)
, (11.9)
поскольку
интеграл
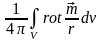 равен нулю. Это следует из следующих
соображений. П
равен нулю. Это следует из следующих
соображений. П оскольку
поверхность S
ограничивает объем V,
то все вихри сосредоточены в этом объеме.
Увеличив объем V на
некоторый слой ΔV,
получим новый объем (V+ΔV),
ограниченный поверхностью SΔ.
Значение объемного интеграла от этого
не изменится, но плотность вихрей на
поверхности SΔ
будет нулевой, и, соответственно, можно
записать:
оскольку
поверхность S
ограничивает объем V,
то все вихри сосредоточены в этом объеме.
Увеличив объем V на
некоторый слой ΔV,
получим новый объем (V+ΔV),
ограниченный поверхностью SΔ.
Значение объемного интеграла от этого
не изменится, но плотность вихрей на
поверхности SΔ
будет нулевой, и, соответственно, можно
записать:
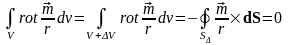 .
.
Для поля :
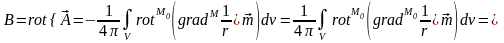
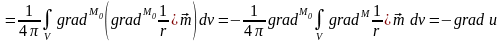 .
.
Результат.
Мы показали, что
,
где
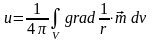 – потенциал поляризованного источника.
Следовательно, во внешнем пространстве
объемный вихрь с плотностью
эквивалентен поляризованному источнику
с плотностью
такой, что
.
При этом следует помнить о том, что из
уравнения
вектор
определяется с точностью до градиента
скалярной функции (
– потенциал поляризованного источника.
Следовательно, во внешнем пространстве
объемный вихрь с плотностью
эквивалентен поляризованному источнику
с плотностью
такой, что
.
При этом следует помнить о том, что из
уравнения
вектор
определяется с точностью до градиента
скалярной функции (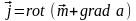 ).
).
