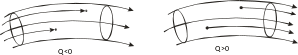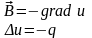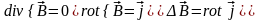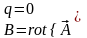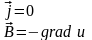6. Классификация полей.

На основании проведенного анализа можем произвести классификацию полей по их структуре, природе и математическому описанию.

			Потенциально во всем пространстве:		Соленоидально во всем пространстве:
q – источники поля		Безвихревое поле:		Лапласово поле: или		Вихревое поле:		– плотность вихрей
			Соленомдально в области, свободной от источников:		Потенциально в области, свободной от вихрей:

Лекция IX. Графическое изображение полей.

(Рекомендуемая литература – Л.М. Альпин. Теория поля)

1. Изображение скалярного поля .

Пусть – однозначная непрерывная функция. Уравнение поверхности (изоповерхность) – поверхность равных значений 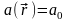. Например, если – температура, то поверхность равных значений – изотермальная поверхность. Совокупность уровенных поверхностей 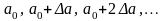создают объемную картину поведения этих поверхностей в пространстве. Для однозначного, непрерывного и убывающего на бесконечности поля уровенные поверхности замкнуты и ни где не пересекаются. Так как объемные карты рисовать трудно, то рисуют сечение уровенных поверхностей на плоскости. Линии, образованные от пересечения уровенных поверхностей с плоскостью, называются уровенными линиями. Часть пространства, заключенного между двумя поверхностями, – уровенный слой. Скалярное поле состоит из уровенных слоев, поэтому его называют ламелларным (lamella – тонкий слой).

В некоторой точке определим градиент поля a по базису, состоящему из орта 1n нормального к уровенной поверхности и двух касательных (тангенсиальных) ортов 1τ₁ и 1τ₂:

, ,

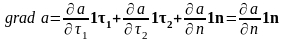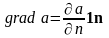т.к. градиент совпадает по направлению с наискорейшем увеличением поля и, соответственно, направлен нормально к уровенной поверхности.

Рассмотрим в точке тонкий уровенный слой. Так как этот слой тонкий, то проведем нормаль к поверхностям, ограничивающим этот слой. Длину нормали, заключенной между двумя поверхностями, назовем толщиной уровенного слоя Δn. Тогда, 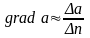и 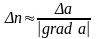. Из последнего соотношения видно, что уровенные поверхности сближаются там, где градиент поля больше, и расходятся, где поле меняется слабо.

2. Графическое изображение векторного поля .

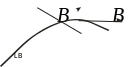Векторное поле 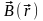можно было бы представить в виде трех скалярных полей 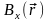, , 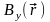, 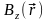и попытаться изобразить поведение каждой скалярной компоненты. Однако, такое изображение полей трудно по восприятию. Поэтому для изображения векторного поля используют векторные линии. Векторная линия поля – это некоторая кривая линия во всех точках которой поле имеет направление касательной к этой линии. Направление векторной линии определяется направлением поля .

Уравнение векторной линии: 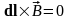, т.к. поле и вектор дифференциала дуги коллиниарны. В декартовом базисе это условие запишется в виде:

.

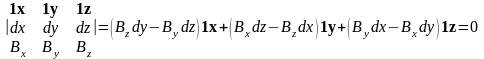В силу линейной независимости ортов:

.

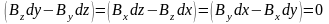Из последнего соотношения следует: 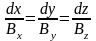. Эта система дифференциальных уравнений 1-го порядка определяет векторную линию.

Если поле однозначно, то векторные линии не пересекаются. Векторные линии могут быть замкнуты, разомкнуты, сходиться в точку и расходиться из точки, уходить в бесконечность. Если поле представляет собой силу, то говорят о силовых линиях, если поле – вихрь, то говорят о вихревых линиях.

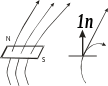Величина поля определяется густотой векторных линий: где поле больше, там линии проходят гуще, где поле меньше, там линии проходят реже. Математически: через площадку ΔS проходит N векторных линий, пропорционально потоку поля через эту площадку: 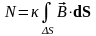. Значение N будет положительно, если вектор нормали к площадке совпадает по направлению с полем.

Пример. Рассмотрим замкнутую поверхность. Поток вихревого поля через эту поверхность будет равен нулю:

.

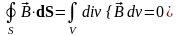
Это означает, что число входящих силовых линий в объем, ограниченной этой поверхностью, равно числу выходящих из него силовых линий.

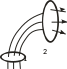
Густота силовых линий говорит о величине поля. В тех местах, где силовые линии сгущаются, там значение поля будет больше. На приведенном рисунке значение поля в пространстве, отмеченном цифрой (1) больше чем в положении (2).

Проведем в пространстве некоторую (невекторную) линию L. Совокупность векторных линий, выходящих из невекторной линии, - в екторная поверхность. В точках векторной поверхности поле не имеет нормальной компоненты. Если L замкнута, то образуется векторная трубка, т.е. векторная трубка – часть пространства, заключенного внутри замкнутой векторной поверхности. В зависимости от характера поля можно говорить о силовой или токовой трубке и, соответственно, о силовой или токовой поверхности.

3. Безвихревое векторное поле в графическом изображении.

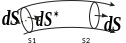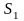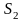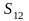Пусть есть поле , удовлетворяющее условиям , т.е поле – поле источников. Рассмотрим векторную трубку, ограниченную двумя нормальными сечениями и , и с боковой поверхностью . Напомним, что поток поля через замкнутую поверхность S равен полной массе источников, находящихся в объеме, ограниченной этой поверхностью: 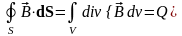. Введем вектор площадку 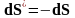, тогда

.

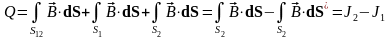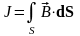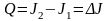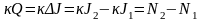Последние два интеграла имеют положительные знаки, поскольку их вектора нормали направлены по полю. Интеграл называется интенсивностью векторной трубки. Таким образом, полная масса источников, заключенных между сечениями и равна разности интенсивностей трубки на этих сечениях: . С учетом того, что число векторных линий, проходящих через площадку ΔS, определяется выражением , можем записать . Если Q положительно (Q>0), то N₂ больше N₁ (N₂ > N₁) и, наоборот, если Q<0, то N₂ < N₁. Это означает, что внутри объема, образованного векторной трубкой, векторные линии либо возникают, начинаясь на положительных источниках, либо исчезают, заканчиваясь на отрицательных источниках.