1. Скалярный потенциал безвихревого поля.

Безвихревое поле удовлетворяет следующим уравнениям:

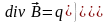или .

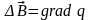Будем обозначать точку интегрирования с координатой через М, а точку наблюдения с координатой через М₀. Тогда, как было показано в предыдущей лекции, решение векторного уравнение Пуассона дается следующим выражением:

.

С учетом того, что плотность вихрей в нашем случае равна нулю, а все источники поля могут находиться в некотором ограниченном объеме V, последний интеграл можно записать в следующем виде:

.

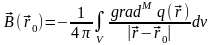При написании этой формулы нами специально указано, что вычисление градиента (дифференцирование) плотности распределения источников q производится по точке интегрирования М.

Покажем, что поле можно определить через некоторую скалярную функцию u, называемую скалярным потенциалом, выраженную через плотность распределения источников q.

Для этого воспользуемся формулой 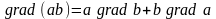. Согласно этой формуле подинтегральное выражение можно представить в виде:

.

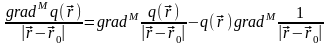Так как 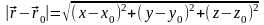, то 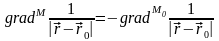, и мы можем записать:

.

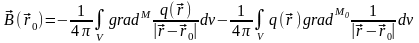Воспользовавшись формулой Остроградского-Гаусса 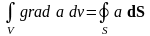, запишем:

.

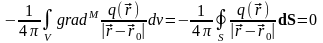Равенство интеграла нулю следует из того, что поверхность S можно взять больше объема V, в котором расположены источники, и, следовательно, плотность источников на этой поверхности будет равна нулю (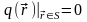 ). В результате:

.

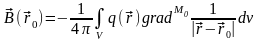Так как в этом интеграле производная берется по точке наблюдения М₀, то знак вычисления градиента можно написать перед знаком интеграла:

.

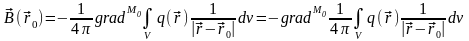Введя функцию 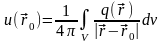, поле можно выразить как ( ).

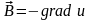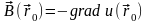Таким образом нами доказано существование некоторого скалярного поля u, градиент которого совпадает с полем . Поле u носит название скалярного потенциала.

Основной результат. С безвихревым векторным полем инвариантно связано поле его потенциалов:

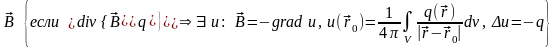. (8.1)

Этот потенциал носит название Ньютонова потенциала, а интеграл, с помощью которого он определяется, – Ньютонова интеграла.

В предыдущей лекции было показано, что 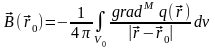, т.е. поле определялось из трех уравнений. Теперь поле можно определить, зная его потенциал, а сам потенциал определяется из одного уравнения.

Определение. Поле, имеющее потенциал, называется потенциальным.

Условие потенциальности: 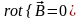(если бы , а поле , то 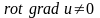, а это невозможно).

Область пространства, в котором – область потенциальности поля .

Безвихревое поле потенциально во всем пространстве. Пример безвихревого поля – поле силы тяжести. Вихревое поле может иметь потенциал только в тех областях, в которых . Примером этого может служить магнитное поле вне тока.

Работа безвихревого поля по любому пути L между двумя точками М₁ и М₂:

.

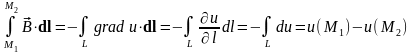Полученный результат показывает, что работа (напряжение) поля равно разности потенциалов в начале и конце пути. Циркуляция поля по замкнутому контуру равна нулю:

.

Как уже отмечалось, вихревое поле может содержать область, в которой поле удовлетворяет условию , и для этих областей можно говорить о потенциальности поля . Однако может оказаться, что потенциал u для этого поля будет неоднозначной функцией. Это будет в случае, если интегрирование производится в неодносвязной области.

2. Векторный потенциал для вихревого поля.

Вихревое поле удовлетворяет следующим уравнениям:

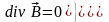или , .

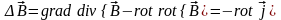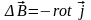Т огда, для поля справедливо следующее уравнение:

.

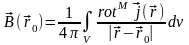Покажем, что можно ввести некоторую векторную функцию, с помощью которой возможно определить поле . Для этого воспользуемся соотношениями 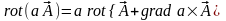, , 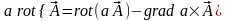и представим интегральное выражение в следующем виде:

.

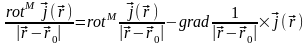Тогда, для поля можно записать:

=

= .

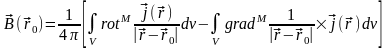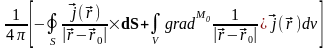Первый интеграл равен нулю, т.к. поверхность S можно взять больше чем поверхность, окружающую объем V, содержащий вихри , и на этой поверхности плотность вихрей будет равна нулю ( ):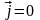

.

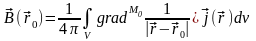Добавим к этому равенству слагаемое 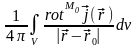, поскольку оно равно нулю. Это следует из того, что плотность вихрей является функцией от и не зависит от , и, поэтому, .

=

= =

= .

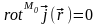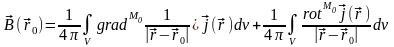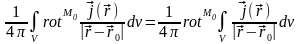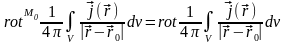Определим векторную функцию : 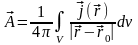. Тогда .

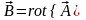Поле носит название векторного потенциала. Его структура соответствует Ньтоновскому потенциалу. Однако поле определяется неоднозначно, поскольку справедливо следующее соотношение:

,

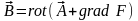где F – любая дифференцируемая функция.

Для того чтобы векторный потенциал определять однозначно, следует на него наложить ограничения. Ранее было показано, что функция из условий

определяется однозначно. Следовательно, для однозначного определения функции следует наложить ограничения на . Наложение ограничений на носит название калибровкой векторного потенциала, а само условие – калибровочным. Для нашего случая оптимальной калибровкой будет условие 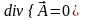. Это условие носит название калибровки Кулона.

Покажем, что в этом случае потенциал определяется однозначно. Для этого рассмотрим выражение 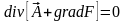. Из этого соотношения следует, что 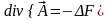. Рассмотрим, чему равно :

,

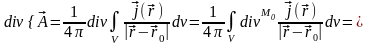воспользовавшись соотношением 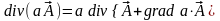, получим

.

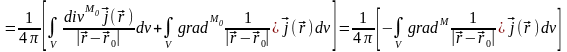Это справедливо, поскольку 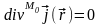. Обратим внимание на то, что из тождества 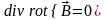следует, что 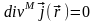. Тогда:

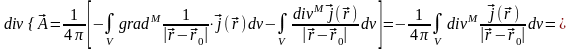
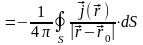= 0.

Интеграл, выписанный в последней строке, равен нулю по той причине, что поверхность S, ограничивающую объем V, можно взять такой, что на ней .

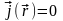Из условия следует, что 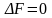. Условию удовлетворяют гармонические функции. Предположив относительно функции F, что она гармонична во всем пространстве и исчезает на бесконечности, получим, согласно теореме о тождественном нуле, что F ≡ 0. Следовательно, векторный потенциал в предположении, что , определяется однозначно:

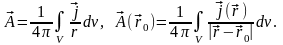
Основной результат. С вихревым полем инвариантно связано векторное поле его векторного потенциала . Калибровка Кулона обеспечивает однозначность определения этой функции, и векторный потенциал удовлетворяет уравнениям:

, .

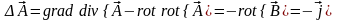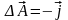Итог выкладок:

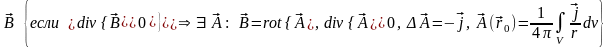. (8.2)

3. Соленоидальное векторное поле.

Поле, имеющее векторный потенциал, - соленоидальное векторное поле. Условие соленоидальности: 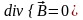. Это условие – условие существования векторного потенциала. Вихревое поле соленоидально во всем пространстве. Это следует из того, что скалярный поток соленоидального поля через любую замкнутую поверхность будет равен нулю: .

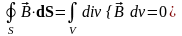Безвихревое поле может иметь области, свободные от источников, где оно будет солиноидальным.

4. Лапласово поле.

В областях, где удовлетворяются условия:

поле потенциально и соленоидально. В этих областях поле называется Лапласовым полем, т.к. оно одновременно удовлетворяет условиям: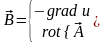 и, следовательно, удовлетворяет уравнениям: 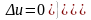. В этой области оба потенциала удовлетворяют уравнению Лапласа.

5. Принцип суперпозиции полей.

В общем случае поле 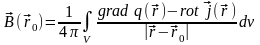. Если поле возбуждается совокупностью источников 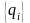и вихрей 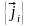, то

.

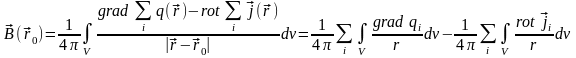Поле – совокупность полей источников и вихрей, возбуждаемых каждым из этих источников и вихрей в отдельности.