
- •4. Дифференцирование векторного поля.
- •6. Теоремы Грина.
- •12. Цилиндрическая система координат.
- •Цикл II. Физическое поле.
- •1. Скалярный потенциал безвихревого поля.
- •6. Классификация полей.
- •1. Изображение скалярного поля .
- •2. Графическое изображение векторного поля .
- •4. Вихревое поле в графическом изображении.
- •2. Поле дипольного источника.
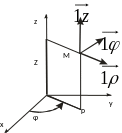
12. Цилиндрическая система координат.
Рассмотрим две наиболее часто употребляемые частные случаи системы криволинейных координат. И первая система – цилиндрическая система координат.
В этой системе выполняются следующие соотношения:
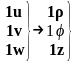
 ;
; 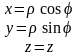 ;
;
При этом орты {1, 1, 1z} образуют правую тройку. Положение точки M определяется через координаты (ρ, φ, z). Коэффициенты Ламэ для этой системы будут иметь следующие выражения:
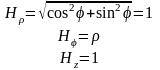 ,
или
,
или
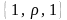 .
.
13. Сферическая система коордиат.
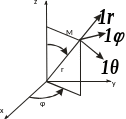 Сферическая
система координат водится согласно
рисунку.
Сферическая
система координат водится согласно
рисунку.
Для этой системы:
 ;
; 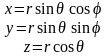
Положение
точки M в этой системе
определяется значениями (r,
, φ). В отличии
от географической системы, отсчеты
координаты
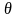 осуществляются от “северного” полюса
в сторону “южного”. И так как координата
z определяется в этом
случае через косинус угла (в отличии от
гегографической широты), то этот угол
носит название кошироты.
осуществляются от “северного” полюса
в сторону “южного”. И так как координата
z определяется в этом
случае через косинус угла (в отличии от
гегографической широты), то этот угол
носит название кошироты.
Коэффициенты
Ламэ для этой системы: 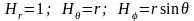 .
.
С некоторыми примерами других систем криволинейных координат можно познакомиться в книге Арго «Математика для электро- и радиоинженеров».
Цикл II. Физическое поле.
Этот раздел посвящен изучению полей, создаваемых элементарными моделями, с помощью которых можно описать реально наблюдаемые физические поля. Для этого необходимо выяснить основные закономерности этих модельных полей.
Лекция VI. Возбудители поля.
Сформулируем 3 фундаментальные аксиомы о физическом поле:
1. Поле возникает в результате действия особых физических объектов. Если нет этих объектов, то нет и поля. Эти объекты – возбудители поля.
2. Возбудители поля занимают ограниченную часть пространства.
3. Поле распределено вблизи возбудителей поля и непрерывно убывает до нуля при удалении от возбудителей.
Эти аксиомы – обобщение нашего опыта. Дальнейшее изложение будет строго математическим.
Основные определения и теоремы.
1 . Если
в какой-то области V
скалярное поле u
удовлетворяет уравнению Лапласа Δu
= 0, то говорят, что функция u
в области V гармонична.
Область V – область
гармоничности функции u.
. Если
в какой-то области V
скалярное поле u
удовлетворяет уравнению Лапласа Δu
= 0, то говорят, что функция u
в области V гармонична.
Область V – область
гармоничности функции u.
2. Лемма
о регулярности гармонической функции
на бесконечности. Если функция u
гармонична вне замкнутой поверхности
S и исчезает на
бесконечности, то при достаточно больших
r (r
> r0)
имеют место соотношения:
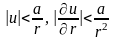 .
Если функция u ведет
себя таким образом, то говорят, что она
регулярна на бесконечности.
.
Если функция u ведет
себя таким образом, то говорят, что она
регулярна на бесконечности.
3. Теорема о тождественном нуле (без доказательства). Если функция u гармонична во всем пространстве и убывает на бесконечности, то она тождественно равно нулю. (Доказательство этой теоремы можно посмотреть в учебнике А.Н. Тихонова и А.А. Самарского «Уравнения математической физики»).
Докажем две теоремы единственности.
Теорема
1. Если скалярное поле a
непрерывно вместе со своими производными
во всем пространстве и убывает на
бесконечности, то задача определения
этого поля из уравнения
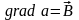 имеет
единственное решение.
имеет
единственное решение.
Доказательство.
Доказательство будем проводить от
противного. Пусть есть два решения
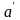 и
и
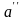 .
Рассмотрим разность
.
Рассмотрим разность
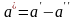 .
Тогда
.
Тогда
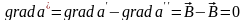 .
.
Отсюда
следует, что
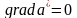 ,
,
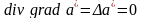 .
По условию теоремы поле a
исчезает на бесконечности, следовательно,
поле
.
По условию теоремы поле a
исчезает на бесконечности, следовательно,
поле
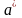 так
же убывает на бесконечности и удовлетворяет
уравнению Лапласа во всем пространстве.
На основании теоремы о тождественном
нуле следует, что
так
же убывает на бесконечности и удовлетворяет
уравнению Лапласа во всем пространстве.
На основании теоремы о тождественном
нуле следует, что
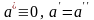 .
.
Теорема 2. Если векторное поле непрерывно вместе со своими частными производными во всем пространстве и исчезает на бесконечности, то задача определения этого поля из системы уравнений:
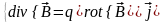 ,
,
имеет единственное решение.
Доказательство.
Как и при доказательстве теоремы 1,
будем исходить от противного. Пусть
есть два решения этой системы
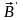 и
и
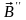 .
Рассмотрим разность
.
Рассмотрим разность
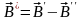 .
Тогда
.
Тогда
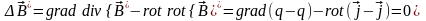 .
.
Разложим
вектор
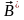 по декартовому базису:
по декартовому базису:
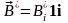 ,
i = x,
y, z.
Тогда
,
i = x,
y, z.
Тогда
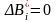 .
В силу условий налагаемых на поле
следует, что
.
В силу условий налагаемых на поле
следует, что
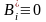 ,
и, следовательно,
,
и, следовательно,
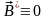 ,
,
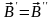 .
.
Основные выводы из теорем единственности. 1. Градиент скалярного поля несет полную информацию об этом поле. 2. Дивергенция и ротор векторного поля несут полную информацию об этом поле. 3. Лапласиан скалярного поля Δu и лапласиан векторного поля также несут полную информацию об этих полях.
Если поле во всем пространстве удовлетворяет условиям:
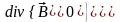 ,
,
то
поле
тождественно равно нулю (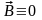 ),
т.е отсутствует. Следовательно, нет
возбудителей поля
.
Поле появляется тогда, когда
),
т.е отсутствует. Следовательно, нет
возбудителей поля
.
Поле появляется тогда, когда
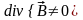 или
или
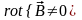 .
Таким образом, скалярные объекты q
и векторные объекты
.
Таким образом, скалярные объекты q
и векторные объекты
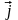 характеризуют возбудители поля, и
существование поля связано с этими
двумя объектами.
характеризуют возбудители поля, и
существование поля связано с этими
двумя объектами.
Для уяснения смысла величин q и рассмотри две гидродинамические модели.
С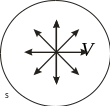 калярные
возбудители поля. Пусть безграничное
пространство заполнено жидкостью с
плотностью m = 1, и пусть
в некотором дифференциально малом
объеме dv за каждую
единицу времени возникает новая порция
жидкости dQ. Т.к.
плотность жидкости m
равна 1, то dQ соответствует
объему. Будет происходить истечение
жидкости, и вектор скорости истечения
жидкости будет направлен по радиусу -
калярные
возбудители поля. Пусть безграничное
пространство заполнено жидкостью с
плотностью m = 1, и пусть
в некотором дифференциально малом
объеме dv за каждую
единицу времени возникает новая порция
жидкости dQ. Т.к.
плотность жидкости m
равна 1, то dQ соответствует
объему. Будет происходить истечение
жидкости, и вектор скорости истечения
жидкости будет направлен по радиусу -
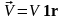 .
Возьмем сферическую поверхность S
и определим объем жидкости, протекающую
через эту поверхность за единицу времени:
.
Возьмем сферическую поверхность S
и определим объем жидкости, протекающую
через эту поверхность за единицу времени:
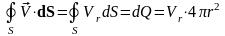 .
.
Из
полученного равенства получаем, что
поле скорости истечения жидкости
определяется соотношением
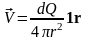 .
.
Исследуем полученное поле скоростей. Для этого определи дивергенцию и ротор этого поля. Так как поле скоростей является сферически симметричным, то вычисления будем проводить в сферической системе координат:
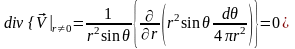 ,
,
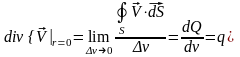 .
.
dQ
– объемность или масса источника, q
– плотность источника. Для всего объема
v –
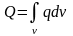 .
Если q>0, то говорят
об источнике, при q<0
– о стоке, или о расхождении и схождении
жидкости (дивергенция – расхождение).
.
Если q>0, то говорят
об источнике, при q<0
– о стоке, или о расхождении и схождении
жидкости (дивергенция – расхождение).
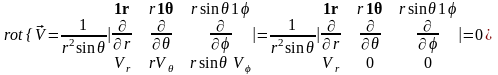 .
.
Ротор поля скоростей для этого случая всюду равен нулю.
Поместим
в область S гребное
колесико с лопастями. Тогда на элемент
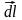 окружности колесика действует вращательный
момент
окружности колесика действует вращательный
момент
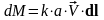 ,
где a – радиус колесика,
k – некоторый коэффициент
пропорциональности. Полный момент,
действующий на колесико –
,
где a – радиус колесика,
k – некоторый коэффициент
пропорциональности. Полный момент,
действующий на колесико –
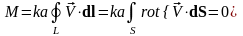 ,
таким образом, колесико в этом потоке
не вращается.
,
таким образом, колесико в этом потоке
не вращается.
Поля,
удовлетворяющие уравнениям
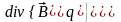 ,
рассматриваются как поле источников,
а скалярные объекты, возбуждающие эти
поля называются источниками.
,
рассматриваются как поле источников,
а скалярные объекты, возбуждающие эти
поля называются источниками.
Следствия. 1) Скалярный поток поля через любую замкнутую поверхность равен полной массе источников, находящихся в объеме:
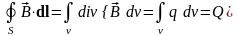 .
.
2) Циркуляция вектора по любому замкнутому контуру равна нулю:
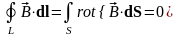 .
.
В екторные
возбудители поля. Пусть безграничное
пространство заполнено несжимаемой
жидкостью. Размешаем эту жидкость так,
что она будет вращаться с постоянной
угловой скоростью
вокруг оси Z. Введем
в рассмотрение векторный объект
екторные
возбудители поля. Пусть безграничное
пространство заполнено несжимаемой
жидкостью. Размешаем эту жидкость так,
что она будет вращаться с постоянной
угловой скоростью
вокруг оси Z. Введем
в рассмотрение векторный объект
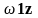 .
Вектор скоростей вращающейся жидкости
в цилиндрической системе координат
будут иметь только
- компоненту:
.
Вектор скоростей вращающейся жидкости
в цилиндрической системе координат
будут иметь только
- компоненту:
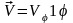 ,
где
,
где
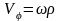 .
Таким образом
.
Таким образом
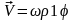 .
.
Определим дивергенцию и ротор полученного поля скоростей:
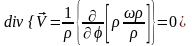 .
.
Полученный результат говорит о том, что данное поле скоростей не имеет источников.
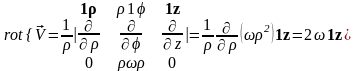 .
.
Таким
образом, ротор исследуемого поля
скоростей отличен от нуля:
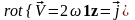 .
Величина
.
Величина
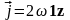 характеризует некоторый объект,
порождающий поле скоростей. Этот объект
носит название вихря, и
-
плотность вихря.
характеризует некоторый объект,
порождающий поле скоростей. Этот объект
носит название вихря, и
-
плотность вихря.
Поместим
гребное колесико в данное поле. Суммарный
момент сил, действующих на это колесико,
будет отличен от нуля и равен
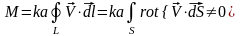 .
Момент М максимален, когда ось Z
совпадает по направлению с осью колеса,
и скорость вращения колесика в любой
точке объема будет одной и той же.
.
Момент М максимален, когда ось Z
совпадает по направлению с осью колеса,
и скорость вращения колесика в любой
точке объема будет одной и той же.
 Реальное
поле может являться суперпозицией полей
разной природы, и по внешнему виду поля
не всегда удается сказать, какими
источниками оно вызвано. Рассмотрим
следующий пример: по каналу течет вода.
Введем ось Х совпадающую с серединой
канала и направленную вдоль течения
воды, а ось Y ей
перпендикулярно. Пусть скорость течения
воды подчиняется следующему закону:
Реальное
поле может являться суперпозицией полей
разной природы, и по внешнему виду поля
не всегда удается сказать, какими
источниками оно вызвано. Рассмотрим
следующий пример: по каналу течет вода.
Введем ось Х совпадающую с серединой
канала и направленную вдоль течения
воды, а ось Y ей
перпендикулярно. Пусть скорость течения
воды подчиняется следующему закону:
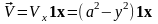 .
Это означает, что течение в канале
прямоструйное, и скорость течения
максимальна в середине канала. Определим
источники и вихри этого поля скоростей:
.
Это означает, что течение в канале
прямоструйное, и скорость течения
максимальна в середине канала. Определим
источники и вихри этого поля скоростей:
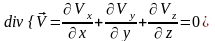 ,
,
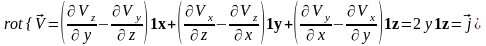 .
.
Полученные результаты показывают, что данное поле скоростей не имеет источников, а создается вихрями. Максимальная плотность вихрей у берегов. Поле скоростей закручивается таким образом, что создается прямоструйное течение.
В
полях создаваемых источниками, т.е. в
полях удовлетворяющих уравнениям
распределение плотности q
может быть любым. Возникает вопрос, а
поведение поля
так
же может быть любым? Для ответа на этот
вопрос рассмотри дивергенцию поля
:
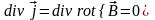 .
Полученный результат говорит о том, что
поле
не имеет источников, и само является
вихревым полем.
.
Полученный результат говорит о том, что
поле
не имеет источников, и само является
вихревым полем.
Следствия. 1) Скалярный поток вихревого поля через замкнутую поверхность равен нулю:
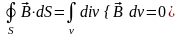 .
.
2) Циркуляция вихревого поля по замкнутому контуру L равна потоку плотности вихря через поверхность S, ограниченную этим контуром:
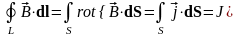 .
.
Лекция VII. Уравнения поля.
Рассмотрим
скалярное поле u,
исчезающее на бесконечности, и определим
его градиент
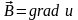 .
Рассмотрим дивергенцию этого поля:
.
Рассмотрим дивергенцию этого поля:
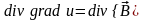 или
или
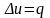 .
Последнее уравнение – скалярное
уравнение Пуассона. Оно имеет
единственное решение. Докажем это.
Пусть есть два решения
.
Последнее уравнение – скалярное
уравнение Пуассона. Оно имеет
единственное решение. Докажем это.
Пусть есть два решения
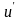 и
и
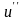 .
Рассмотрим разность
.
Рассмотрим разность
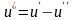 .
Тогда
.
Тогда
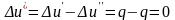 .
.
В
силу условий налагаемых на u
следует, что
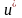 – функция гармоническая во всем
пространстве и исчезающая на бесконечности.
Согласно теореме о тождественном нуле
(лекция VI),
– функция гармоническая во всем
пространстве и исчезающая на бесконечности.
Согласно теореме о тождественном нуле
(лекция VI),
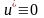 ,
и, следовательно,
,
и, следовательно,
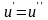 .
.
Рассмотрим
векторное поле
.
Оно удовлетворяет условиям
,
т.е. содержит как вихревую, так и
безвихревую части. Для лапласиана этого
поля справедлива следующая запись:
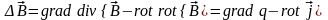 .
Введем обозначение
.
Введем обозначение
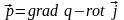 .
Тогда,
.
Тогда,
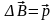 .
В декартовой системе координат последнее
уравнение распадается на три уравнения:
.
В декартовой системе координат последнее
уравнение распадается на три уравнения:
 или
или
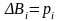 ,
где i = x,
y, z,
т.е. состоит из трех скалярных уравнений
Пуассона. Это означает, что для
нахождения поля
надо знать плотность источников и
вихрей.
,
где i = x,
y, z,
т.е. состоит из трех скалярных уравнений
Пуассона. Это означает, что для
нахождения поля
надо знать плотность источников и
вихрей.
Таким образом, характер скалярного или векторного поля определяется из решения скалярного уравнения Пуассона. Для того чтобы решить уравнение введем в рассмотрение следующие три функции – функцию включения, функцию Дирака, функцию Грина.
1 .
Функция включения. Эта функция была
введена в рассмотрение Хевисайдом, и
ее часто называют его именем, т.е. функцией
Хевисайда. Эту функцию можно
рассматривать как результат предельного
перехода следующей функции:
.
Функция включения. Эта функция была
введена в рассмотрение Хевисайдом, и
ее часто называют его именем, т.е. функцией
Хевисайда. Эту функцию можно
рассматривать как результат предельного
перехода следующей функции:
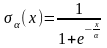 .
.
При
α → 0
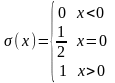 .
.
Смещенная функция включения определяется следующим соотношением:
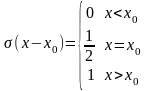 .
.
2. Функция Дирака. Эта функция впервые появилась в квантовой механике, и может быть определена как предельный переход следующей функции:
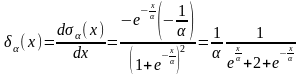 .
.
Характер поведения этой функции в зависимости от х будет следующим:
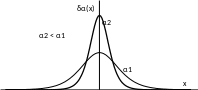
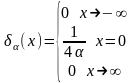 .
.
При α→0 получим бесконечно тонкий импульс:
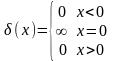 .
.
Полученная функция носит название функции Дирака (импульс Дирака). Смещенная функция Дирака имеет вид:
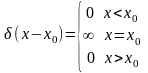 .
.
Замечание. Функцию Дирака мы ввели как производную функции Хевисайда, хотя сама функция Хевисайда не имеет производной в точке x = 0. Такие функции носят название обобщенных функций.
Рассмотрим
интеграл
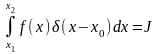 ,
где
,
где
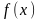 – непрерывная функция. Интеграл будем
брать по частям (
– непрерывная функция. Интеграл будем
брать по частям (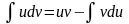 ):
):
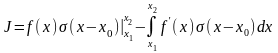 .
.
Возможны три случая: 1-й – х0<x1, 2-й – x1<х0<x2, 3-й – х0>x2:
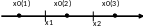
1. 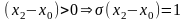 ,
,
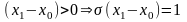 ,
,
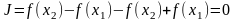 .
.
2.
,
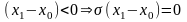 ,
,
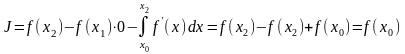 .
.
3. 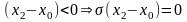 ,
,
,
,
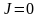 .
.
Таким
образом
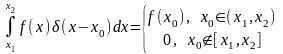 .
.
(Вопрос – Чему равен интеграл на границе области?).
Частный
случай –
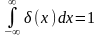 .
Площадь импульса равна 1, поэтому эту
функцию называют единичным импульсом.
.
Площадь импульса равна 1, поэтому эту
функцию называют единичным импульсом.
Трехмерная
функция Дирака –
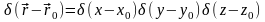 .
Очевидно,
.
Очевидно,
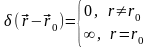 .
Рассмотрим объемный интеграл
.
Рассмотрим объемный интеграл
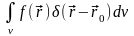 .
Ограничимся случаями, когда линия,
параллельная координатной оси, пересекает
область v только
в двух точках. Тогда:
.
Ограничимся случаями, когда линия,
параллельная координатной оси, пересекает
область v только
в двух точках. Тогда:
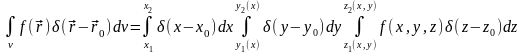 .
.
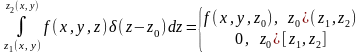 ,
,
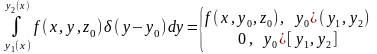 ,
,
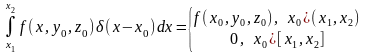 .
.
Окончательно
можно записать:
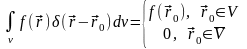 (7.1).
(7.1).
3 . Функция
Грина для уравнения Пуассона.
. Функция
Грина для уравнения Пуассона.
Пусть
в пространстве расположены две точки
– М и М0.
Функция Грина – функция взаимного
расположения двух точек:
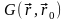 .
Иногда эту функцию записывают в виде
.
Иногда эту функцию записывают в виде
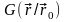 .
Функция взаимного расположения точек
определяется разностью векторов
.
Функция взаимного расположения точек
определяется разностью векторов
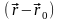 и должна удовлетворять уравнению
Пуассона
и должна удовлетворять уравнению
Пуассона
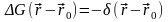 .
В общем случае это уравнение не имеет
единственного решения. Наложим ограничения
на функцию
.
В общем случае это уравнение не имеет
единственного решения. Наложим ограничения
на функцию
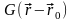 – предадим ей смысл поля: функция убывает
на бесконечности и обладает сферической
симметрией:
– предадим ей смысл поля: функция убывает
на бесконечности и обладает сферической
симметрией:
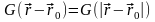 ,
,
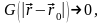 при
при
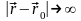 .
.
Поместим
начало отсчета в точку
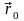 .
Тогда
.
Тогда
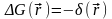 .
В сферической системе координат это
уравнение приобретет вид:
.
В сферической системе координат это
уравнение приобретет вид:
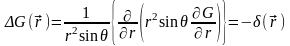 .
.
При
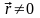 имеем:
имеем:
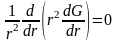 .
Далее, из этого уравнения получаем:
.
Далее, из этого уравнения получаем:
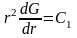 ,
,
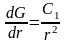 ,
,
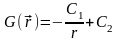 .
.
Из условия убывания функции G на бесконечности следует, что С2 = 0. Найдем константу С1:
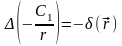 ,
,
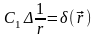 .
.
Рассмотрим сферическую область V. Тогда
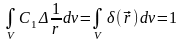 ,
,
т.к.
точка
находится внутри области V
(формула 7.1). Отсюда следует, что
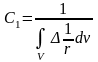 ;
;
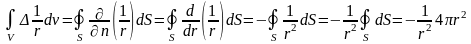 ,
,
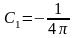 .
.
Таким
образом, функция Грина будет для данного
случая иметь вид
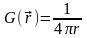 .
Сместив точку
из начала координат, окончательно
получим
.
Сместив точку
из начала координат, окончательно
получим
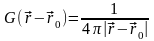
– фундаментальная функция Грина для уравнения Пуассона.
Вернемся к решению скалярного уравнения Пуассона . Для решения этого уравнения воспользуемся второй формулой Грина:
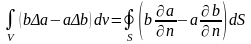 .
.

Поместим
начало отсчета в точку M0
(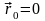 )
и проведем из этой точки сферическую
поверхность радиуса
.
Положим
)
и проведем из этой точки сферическую
поверхность радиуса
.
Положим
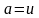 и
и
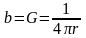 :
:
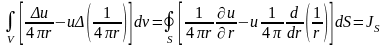 ,
,
т.к.
,
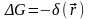 ,
то
,
то
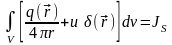 .
.
Из
условия
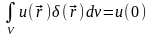 следует, что
следует, что
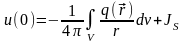 .
Обозначим через qi
источники внутри области V
и через qe
– внешние по отношению к области V.
Тогда интеграл в последнем уравнении
представляет собой сумму воздействия
всех внутренних источников, а второе
слагаемое – действие всех внешних
объемных источников, сведенных к действию
некоторого источника, распределенного
по поверхности сферы (эквивалентная
замена внешних объемных источников
поверхностным).
.
Обозначим через qi
источники внутри области V
и через qe
– внешние по отношению к области V.
Тогда интеграл в последнем уравнении
представляет собой сумму воздействия
всех внутренних источников, а второе
слагаемое – действие всех внешних
объемных источников, сведенных к действию
некоторого источника, распределенного
по поверхности сферы (эквивалентная
замена внешних объемных источников
поверхностным).
Устремим
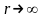 ,
при этом все источники окажутся внутри
нашей сферы. Что произойдет с интегралом
JS?
Рассмотрим этот случай:
,
при этом все источники окажутся внутри
нашей сферы. Что произойдет с интегралом
JS?
Рассмотрим этот случай:
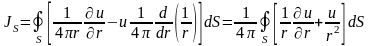 .
.
Оценим полученный интеграл:
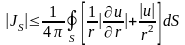 .
.
Воспользовавшись понятием регулярности функции u на бесконечности (Лемма о регулярности гармонической функции на бесконечности: если функция u гармонична вне замкнутой поверхности S и исчезает на бесконечности, то при достаточно больших r (r > r0) имеют место соотношения: . Если функция u ведет себя таким образом, то говорят, что она регулярна на бесконечности), получим:
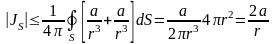 .
.
Так
как
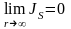 ,
то
,
то
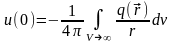 .
Окончательно можно записать:
.
Окончательно можно записать:
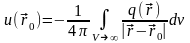 . (7.2)
. (7.2)
Полученный результат является решением скалярного уравнения Пуассона.
Решение векторного уравнения Пуассона , где . Для решения воспользуемся декартовым базисом. Тогда , где i = x, y, z, и
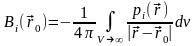 ,
,
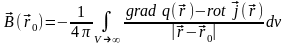 .
.
Лекция VIII. Потенциалы векторного поля.
