
- •4. Дифференцирование векторного поля.
- •6. Теоремы Грина.
- •12. Цилиндрическая система координат.
- •Цикл II. Физическое поле.
- •1. Скалярный потенциал безвихревого поля.
- •6. Классификация полей.
- •1. Изображение скалярного поля .
- •2. Графическое изображение векторного поля .
- •4. Вихревое поле в графическом изображении.
- •2. Поле дипольного источника.
6. Теоремы Грина.
Для вывода первой теоремы Грина воспользуемся теоремой Остроградского – Гаусса .
Пусть
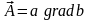 .
Тогда
.
Тогда
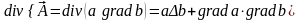 ,
,
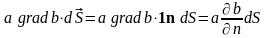 ;
;
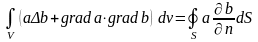 . (4.8)
. (4.8)
Для вывода второй формулировки теоремы Грина перепишем уравнение (4.8), поменяв местами функции a и b:
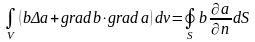 ,
,
Вычтя полученное уравнение из уравнения (4.8) получим вторую формулировку теоремы:
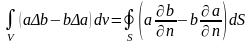 . (4.9)
. (4.9)
Лекция V. Криволинейные координатные системы.
В лекциях по высшей математике вы должны были познакомиться с сферической и цилиндрической системой координат. Это частные случаи криволинейной координатной системы. Помимо сферической и цилиндрической существует еще множество различных координатных систем, которые вводятся в зависимости от типа решаемой задачи.
1. Основные определения.
 Рассмотрим
декартову систему координат. В этой
системе положение какой-либо точки M
определяются координатами (x,
y, z).
Пусть заданы функции
Рассмотрим
декартову систему координат. В этой
системе положение какой-либо точки M
определяются координатами (x,
y, z).
Пусть заданы функции
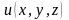 ,
,
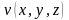 ,
,
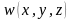 ,
и эти функции образуют взаимно-однозначную
систему со своими аргументами
,
и эти функции образуют взаимно-однозначную
систему со своими аргументами
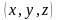 .
Это означает, что можно создать систему
функций, аргументами которой будут
значения
.
Это означает, что можно создать систему
функций, аргументами которой будут
значения
![]() –
–
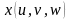 ,
,
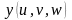 ,
,
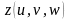 .
Это означает также, что положение точки
M можно выразить через
значения функций
.
Это означает также, что положение точки
M можно выразить через
значения функций
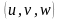 – M
.
– M
.
Можно
зафиксировать значения функций u,
v, w,
положив их равным некоторым константам:
![]() ,
,
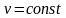 ,
,
![]() .
В результате будут образованы некоторые
поверхности, которые будут координатными
поверхностями. Пересечение координатных
поверхностей дадут координатные линии.
Так, пересечение поверхностей
.
В результате будут образованы некоторые
поверхности, которые будут координатными
поверхностями. Пересечение координатных
поверхностей дадут координатные линии.
Так, пересечение поверхностей
![]() и
дадут u-линию, поверхности
и
и
дадут u-линию, поверхности
и
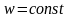 дадут
v-линию и поверхности
и
– w-линию. Если
полученные таким образом линии будут
кривыми, то полученная система называется
криволинейной. Если же эти линии в каждой
точке пространства взаимно ортогональны,
то полученная система называется
ортогональной криволинейной системой.
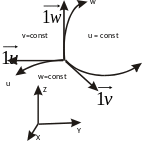
Это означает, что в каждой точке
пространства существует ортогональный
локальный базис {1u,
1v, 1w}.
Направление ортов этого базиса может
меняться в пространстве, т.е. орты
локального базиса – переменные вектора.
Этот базис подвижен. В отличие от
локального базиса, декартовый (центральный)
базис не меняет направления ортов
базиса. Следовательно, центральный
базис неподвижен, и он является основным.
дадут
v-линию и поверхности
и
– w-линию. Если
полученные таким образом линии будут
кривыми, то полученная система называется
криволинейной. Если же эти линии в каждой
точке пространства взаимно ортогональны,
то полученная система называется
ортогональной криволинейной системой.
Это означает, что в каждой точке
пространства существует ортогональный
локальный базис {1u,
1v, 1w}.
Направление ортов этого базиса может
меняться в пространстве, т.е. орты
локального базиса – переменные вектора.
Этот базис подвижен. В отличие от
локального базиса, декартовый (центральный)
базис не меняет направления ортов
базиса. Следовательно, центральный
базис неподвижен, и он является основным.
2. Коэффициенты Ламэ.
Р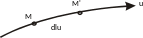 ассмотрим
какую-нибудь криволинейную координатную
линию, например, u-линию.
Возьмем две точки M и
M
расположенные на этой линии на расстоянии
dlu.
Возникает вопрос, какова будет длина
элемента дуги этой линии в зависимости
от изменения параметра u.
ассмотрим
какую-нибудь криволинейную координатную
линию, например, u-линию.
Возьмем две точки M и
M
расположенные на этой линии на расстоянии
dlu.
Возникает вопрос, какова будет длина
элемента дуги этой линии в зависимости
от изменения параметра u.
Что
бы объяснить, о чем идет речь, рассмотрим
полярную систему координат. Положение
точки в этой системе определяется
расстоянием от центральной точки до
точки наблюдения
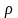 и углом ,
образованным этим радиус-вектором с
осью X. Пусть точка M
имеет координаты
и углом ,
образованным этим радиус-вектором с
осью X. Пусть точка M
имеет координаты
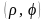 ,
а точка M
–
,
а точка M
–
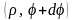 .
Тогда длина дуги dl
между точками M и M
будет равна
.
Тогда длина дуги dl
между точками M и M
будет равна
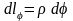 ,
т.е. длина дуги определяется изменением
угла через некоторый метрический
коэффициент, который и носит название
коэффициента Ламэ.
,
т.е. длина дуги определяется изменением
угла через некоторый метрический
коэффициент, который и носит название
коэффициента Ламэ.
Вернемся
к вопросу о длине дуги dlu.
Она будет равна
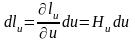 .
Коэффициент
.
Коэффициент
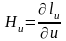 – коэффициент Ламэ. С его помощью
осуществляется перевод приращения
аргумента в расстояние.
– коэффициент Ламэ. С его помощью
осуществляется перевод приращения
аргумента в расстояние.
Получим
выражение коэффициента Ламэ
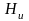 через частные производные:
через частные производные:
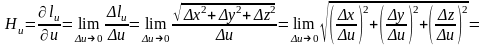
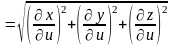 .
.
Аналогичным
образом определяются коэффициенты
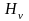 и
и
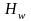 :
:
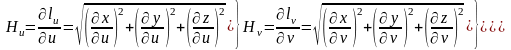 . (5.1)
. (5.1)
3. Переход от центрального базиса к локальному.
Пусть {1x, 1y, 1z} - центральный базис, {1u, 1v, 1w} - локальный. Разложим орт 1u по центральному базису:
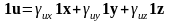 ;
;
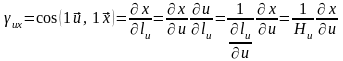 .
.
Таким образом, выражения для направляющих косинусов будут иметь вид:
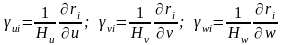 .
.
Переход от центрального базиса к локальному будет определяться соотношением
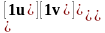 ;
; 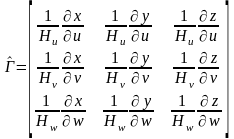 . (5.2)
. (5.2)
Переход от локального базиса к центральному:
; 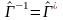 .
.
Преобразование компонент вектора осуществляется с помощью соотношений:
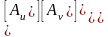 ;
.
;
.
6. Элементы длины, площади и объема.
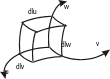 Элементы
дуги, площади и объема в криволинейных
координатах будут определяться
соотношениями:
Элементы
дуги, площади и объема в криволинейных
координатах будут определяться
соотношениями:
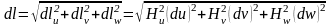 ;
;
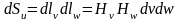 ;
;
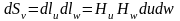 ;
(5.3)
;
(5.3)
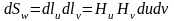 ;
;
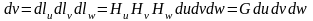 .
.
В
последнем выражении введено обозначение
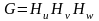 .
.
7. Градиент скалярного поля.
Рассмотрим скалярное поле, зависящее от переменных u, v, w – a(u,v,w). Тогда выражение для градиента этого поля представляется следующим образом:
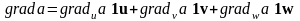 .
.
В
то же время,
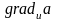 –
это производная скалярного поля a
по направлению
–
это производная скалярного поля a
по направлению
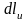 ,
и тогда:
,
и тогда:
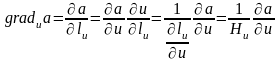 .
.
Аналогичные
соотношения получаются для
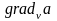 и
и
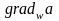 .
В результате:
.
В результате:
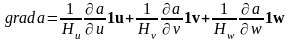 . (5.4)
. (5.4)
8. Дивергенция векторного поля.
Для вывода выражения дивергенции векторного поля в криволинейных координатах воспользуемся полученным в четвертой лекции инвариантным определением дивергенции (4.4):
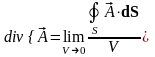 .
.
Д ля
этого выделим в точке с координатами
(u,v,w)
элементарный прямоугольник со сторонами
,
ля
этого выделим в точке с координатами
(u,v,w)
элементарный прямоугольник со сторонами
,
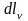 и
и
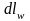 .
Выражение для объема V
этого прямоугольника нами уже было
получено:
.
Выражение для объема V
этого прямоугольника нами уже было
получено:
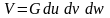 .
.
Рассмотрим,
чему будет равен скалярный поток вектора
через поверхность S,
ограничивающую этот прямоугольник, –
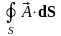 .
Так, поток вектора через поверхность
.
Так, поток вектора через поверхность
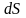 при значении аргумента равном
при значении аргумента равном
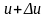 будет равен
будет равен
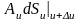 ,
при этом, поскольку вектор нормали 1n
для этой поверхности совпадает с вектором
1u, то этот
поток имеет положительный знак. В то же
время, поток вектора
через поверхность
при
значении аргумента равном u,
будет равен
,
при этом, поскольку вектор нормали 1n
для этой поверхности совпадает с вектором
1u, то этот
поток имеет положительный знак. В то же
время, поток вектора
через поверхность
при
значении аргумента равном u,
будет равен
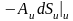 .
Знак “–” для этой стороны появляется
из-за того, что нормаль к этой стороне
направлена в противоположенную сторону
по сравнению с вектором 1u.
Таким же образом будет определяться
поток вектора
через другие стороны:
.
Знак “–” для этой стороны появляется
из-за того, что нормаль к этой стороне
направлена в противоположенную сторону
по сравнению с вектором 1u.
Таким же образом будет определяться
поток вектора
через другие стороны:
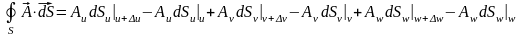 .
.
Рассмотрим первые два слагаемых. Для них можно записать:
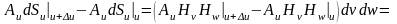 *
*
При
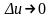 ,
разность, стоящую в скобках, можно
представить в виде производной:
,
разность, стоящую в скобках, можно
представить в виде производной:
*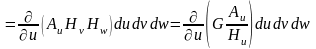 .
.
Аналогичные соотношения можно получить для второй и третьей пары слагаемых. Таким образом, для скалярного потока поля можно записать:
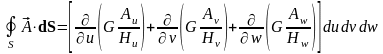 .
.
Окончательно, выражение дивергенции в криволинейной системе координат будет следующим:
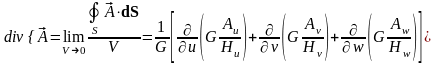 . (5.5)
. (5.5)
9. Ротор векторного поля.
Для вывода выражения для ротора воспользуемся соотношением (4.7):
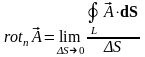 .
.
 В
качестве орта 1n
рассмотрим в начале орт 1u,
затем – орты 1v
и 1w. Для
вычисления проекции ротора на орт 1u
выберем в пространстве точку с координатами
,
и в этой точке зададимся контуром, по
которому будем вычислить циркуляцию
вектора
.
Пусть этот контур лежит в плоскости
В
качестве орта 1n
рассмотрим в начале орт 1u,
затем – орты 1v
и 1w. Для
вычисления проекции ротора на орт 1u
выберем в пространстве точку с координатами
,
и в этой точке зададимся контуром, по
которому будем вычислить циркуляцию
вектора
.
Пусть этот контур лежит в плоскости
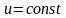 ,
имеет положительное направление обхода,
которое определяется по правилу правого
винта, и представляет собой прямоугольник
со сторонами равными
и
,
которые соответствуют приращению своих
аргументов
,
имеет положительное направление обхода,
которое определяется по правилу правого
винта, и представляет собой прямоугольник
со сторонами равными
и
,
которые соответствуют приращению своих
аргументов
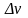 и
и
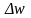 .
.
Площадь такого прямоугольника
будет равна
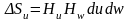 .
.
Циркуляция вектора по контуру, ограничивающему этот прямоугольник будет равна:

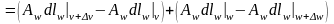 .
.
При расстановке знаков в этом выражении учитывалось направление обхода контура. Если оно совпадало с приращением аргумента, то знак положительный, если же обход совершался в противоположенную сторону, то знак – отрицательный.
Рассмотрим первые два слагаемые:
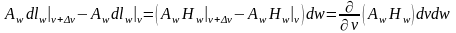 ;
;
Аналогичную записать можно сделать для третьего и четвертого слагаемых:
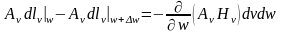 .
.
В результате, для
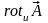 можно записать:
можно записать:
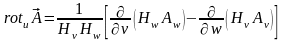 .
.
Точно так же можно получить
выражения для
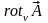 и
и
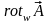 .
.
Окончательное выражение для ротора в криволинейной системе координат будет иметь вид:
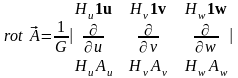 . (5.6)
. (5.6)
10. Лапласиан скалярного поля.
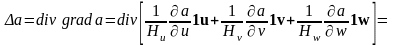
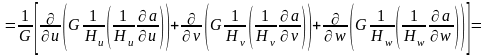
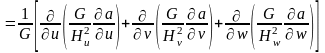 . (5.7)
. (5.7)
11. Лапласиан векторного поля.
Лапласиан векторного поля определяется из выражения:
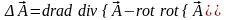 .
.
Это выражение получается достаточно длинным и сложным для запоминания, и хотя вывод его не представляет сложностей, в этом курсе мы этого делать не будем. Полное выражение для лаплассиана векторного поля можно посмотреть в “Cправчнике по математике” авторов Г. Корн и Т. Корн.
