
- •4. Дифференцирование векторного поля.
- •6. Теоремы Грина.
- •12. Цилиндрическая система координат.
- •Цикл II. Физическое поле.
- •1. Скалярный потенциал безвихревого поля.
- •6. Классификация полей.
- •1. Изображение скалярного поля .
- •2. Графическое изображение векторного поля .
- •4. Вихревое поле в графическом изображении.
- •2. Поле дипольного источника.
Вопросы к зачету по теории поля.
1.Сложение и умножение векторов
2.Матрицы,действия над матрицами.
3.Переход от одного базиса к другому.
4.Преобразование компонент вектора при смене базиса
5.Тензор,линейные векторные функции векторного аргумента.
6.Дифференцирование скалярного поля ,понятие градиента,производной скалярного поля по направлению.
7.Оператор Гамильтона(оператор “набла”)
8.Дифференцирование векторного поля.
9.Градиент
скалярных
полей:
grad(a+b), grad(ab),gradF(a), grad(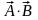 )
)
10.Дивергенция
полей : div(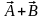 ),div(a
),div(a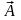 ),
div(
),
div(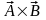 )
)
11.Ротор полей: rot( ), rot(a ), rot( )
12.Вторые производные скалярных и векторных полей , лапласиан скалярного и векторого поля
13.Теорема Остроградского-Гаусса и ее векторные формулировки.
14.Теорема Стокса и ее векторные формулировки.
15.Теоремы Грина.
16.Понятие криволинейных координат, коэффициенты Ламэ.
17.Переход от центрального базиса к локальному и обратно
18.Градиент скалярного поля в криволинейной системе координат.
19.Дивергенция векторного поля в криволинейной системе координат.
20.Ротор в криволинейной системе координат
21.Лапласиан скалярного поля в криволинейной системе координат.
22.Цилиндрическая система координат.
23.Сферическая система координат.
24.Понятие гармонической функции, лемма о регулярности гармонической функции.
25.Теоремы единственности определения скалярной и векторной функции.
26.Скалярные возбудители поля.
27.Векторые возбудители поля.
28.Функция Хевисайда и функция Дирака.
29.Функция Грина для скалярного уравнения Пуассона.
30.Решение скалярного уравнения Пуассона.
31.Решение векторного уравнения Пуассона.
32.Скалярный потенциал безвихревого поля
33.Векторный потенциал вихревого поля
34.Классификация полей.
35.Изображение скалярного поля.
36.Графическое изображение векторного поля.
37.Безвихревое векторное поля в графическом изображении
38.Вихревое поле в графическом изображении
39.Поле точечного источника
40.Поле дипольного источника
41.Линейный источник ,поле однородного прямолинейного источника
42.Бесконечно длинный однородный прямолинейный источник. Логарифмический потенциал
43.Поле однородного кругового цилиндра(кольцо)
44.Поверхностный источник, поле кругового диска. Граничные условия.
45.Бесконечная плоскость с постоянной поверхностью плотностью. Граничные условия.
46.Двойной поверхностный источник(двойной слой ,дипольный слой)
47.Двойной слой в виде диска с ms =const.Граничные условия.
48.Поле однородной сферы
49.Поляризованный объемный источник. Граничные условия.
50.Поле однородно поляризованной сферы.
Лекция II. Алгебра физических величин.
1. Физические
поля бывают скалярные, векторные и
тензорные. Примером скалярного поля
может быть поле температур или поле
плотности. Скалярные величины обычно
будем обозначать строчными буквами -
a, b
и т.п. В отличие от скалярных величин
векторные поля характеризуются величиной
и направлением. Для их обозначения в
этом курсе лекций обычно будем использовать
прописные буквы с символом стрелки над
ними (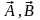 ),
а также прописные или строчные буквы,
выделенные жирным шрифтом (a,
b, A,
dB). Пример векторного
поля – поле силы тяжести, напряженность
электрического поля и т.п. Понятие
тензорного поля мы рассмотрим несколько
позже.
),
а также прописные или строчные буквы,
выделенные жирным шрифтом (a,
b, A,
dB). Пример векторного
поля – поле силы тяжести, напряженность
электрического поля и т.п. Понятие
тензорного поля мы рассмотрим несколько
позже.
2. Алгебра скалярных величин. Основные операции над скалярными величинами – сложение и умножение. Операции обратные сложению и умножению будут соответственно вычитание и деление. Основные свойства:
К)
коммутативность (перестановочность): 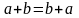 ,
,
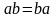 ;
;
А)
ассоциативность (сочетательность): 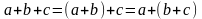 ,
,
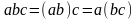 ;
;
Д)
дистрибутивность (распределительность): 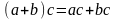 .
.
3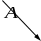 . Алгебра
векторных величин. Вектора графически
изображаются в виде стрелки. Длина
стрелки характеризует абсолютную
величину или модуль вектора
. Алгебра
векторных величин. Вектора графически
изображаются в виде стрелки. Длина
стрелки характеризует абсолютную
величину или модуль вектора
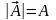 ,
а направление стрелки – направление
действия этой величины (поля). Если
модуль вектора равен 1 (единице), то такой
вектор называют единичным, если нулю –
то нулевым. Если вектор можно перемещать
в пространстве параллельно самому себе
– то такой вектор называют свободным
вектором; если его можно перемещать
только вдоль прямой линии, совпадающей
с вектором, то такой вектор называют
скользящим; если вектор нельзя перемещать
в пространстве, то его называют связным
вектором.
,
а направление стрелки – направление
действия этой величины (поля). Если
модуль вектора равен 1 (единице), то такой
вектор называют единичным, если нулю –
то нулевым. Если вектор можно перемещать
в пространстве параллельно самому себе
– то такой вектор называют свободным
вектором; если его можно перемещать
только вдоль прямой линии, совпадающей
с вектором, то такой вектор называют
скользящим; если вектор нельзя перемещать
в пространстве, то его называют связным
вектором.
Вектора называют коллинеарными, если они направлены вдоль одной прямой. Вектора называют компланарными, если они лежат в одной плоскости.
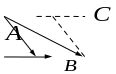
С ложение
векторов. В результате сложения двух
векторов будет получен вектор, являющейся
диагональю параллелограмма со сторонами,
образованными из исходных векторов.
При сложении трех векторов результирующий
вектор будет диагональю параллелепипеда,
стороны которого совпадают со сторонами
исходных векторов. В общем случае при
сложении нескольких векторов результирующий
вектор будет замыкающим ломаной линии,
звенья которой образованы слагаемыми
векторами.
ложение
векторов. В результате сложения двух
векторов будет получен вектор, являющейся
диагональю параллелограмма со сторонами,
образованными из исходных векторов.
При сложении трех векторов результирующий
вектор будет диагональю параллелепипеда,
стороны которого совпадают со сторонами
исходных векторов. В общем случае при
сложении нескольких векторов результирующий
вектор будет замыкающим ломаной линии,
звенья которой образованы слагаемыми
векторами.
У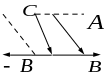 множение
вектора на скаляр – скаляр умножается
на модуль вектора. В результате получается
вектор того же направления, если скаляр
положительный. Если скаляр отрицателен,
то будет получен вектор противоположенного
направления.
множение
вектора на скаляр – скаляр умножается
на модуль вектора. В результате получается
вектор того же направления, если скаляр
положительный. Если скаляр отрицателен,
то будет получен вектор противоположенного
направления.
Вычитание вектора эквивалентно прибавлению вектора противоположенного направления:
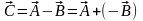 .
.
Основные свойства:
К)
коммутативность (перестановочность): 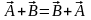 ,
,
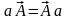 ;
;
А)
ассоциативность (сочетательность): 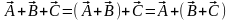 ;
;
Д)
дистрибутивность (распределительность): 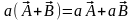 ,
,
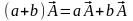 .
.
3. Линейная
комбинация векторов. Под линейной
комбинацией векторов понимают следующую
сумму
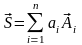 .
Используя соглашение о суммировании,
эту же сумму можно записать в виде
.
Используя соглашение о суммировании,
эту же сумму можно записать в виде
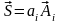 ,
где i=1…n.
Параметр i носит
название немого индекса или индекса
суммирования, а само суммирование при
такой записи осуществляется по дважды
повторяемому индексу.
,
где i=1…n.
Параметр i носит
название немого индекса или индекса
суммирования, а само суммирование при
такой записи осуществляется по дважды
повторяемому индексу.
Вектора
будут линейно зависимы, если их линейная
комбинация будет равна нулю (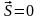 ),
хотя бы при одном ai
не равном нулю (
),
хотя бы при одном ai
не равном нулю (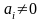 ).
Вектора будут линейно независимы, если
их линейная комбинация будет равна нулю
(
)
только тогда, когда все ai
будут равны нулю (
).
Вектора будут линейно независимы, если
их линейная комбинация будет равна нулю
(
)
только тогда, когда все ai
будут равны нулю (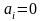 ).
).
Два
вектора будут линейно зависимы, если
они коллинеарны (лежат вдоль одной
прямой). Три линейно зависимых вектора
компланарны (лежат в одной плоскости).
Четыре вектора всегда линейно зависимы,
поскольку любой из этих векторов можно
представить как диагональ параллелограмма,
построенного с помощью других трех
векторов:
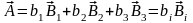 ,
где i = 1, 2, 3.
,
где i = 1, 2, 3.
4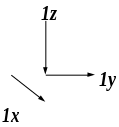 . Ортонормированный
базис. Три линейно независимых вектора
образуют базис. Если эти вектора
ортогональны, то такой базис называется
ортогональным базисом. Если эти вектора
к тому же еще и единичны, то такой базис
называют ортонормированным декартовым
базисом. Будем обозначать эти вектора
(орты) следующим образом:
. Ортонормированный
базис. Три линейно независимых вектора
образуют базис. Если эти вектора
ортогональны, то такой базис называется
ортогональным базисом. Если эти вектора
к тому же еще и единичны, то такой базис
называют ортонормированным декартовым
базисом. Будем обозначать эти вектора
(орты) следующим образом:
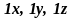 .
Будем так же предполагать, что эти
вектора образуют правую тройку.
.
Будем так же предполагать, что эти
вектора образуют правую тройку.
Любой вектор можно представить в виде линейной комбинации ортов:
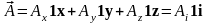 ,
где i = x,
y, z.
,
где i = x,
y, z.
Ax,
Ay,
Az
носят название скалярных компонент
вектора,
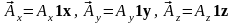 – векторные компоненты вектора
.
Сам вектор
является диагональю прямоугольного
параллелепипеда, построенного на
векторных компонентах.
– векторные компоненты вектора
.
Сам вектор
является диагональю прямоугольного
параллелепипеда, построенного на
векторных компонентах.
Докажем
единственность разложения вектора в
ортонормированном базисе. Пусть вектор
имеет два различных разложения:
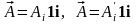 ,
i = x,
y, z.
Вычтя из первого разложения второе,
получим
,
i = x,
y, z.
Вычтя из первого разложения второе,
получим
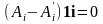 .
Так как орты линейно независимы, то
отсюда следует, что коэффициенты
.
Так как орты линейно независимы, то
отсюда следует, что коэффициенты
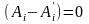 ,
и, следовательно,
,
и, следовательно,
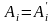 .
Тем самым доказана единственность
разложения вектора в ортонормированном
базисе.
.
Тем самым доказана единственность
разложения вектора в ортонормированном
базисе.
5. Сложение и вычитание векторов будет являться сложением и вычитанием компонент этих векторов:
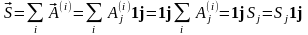 ,
где j = x,
y, z.
,
где j = x,
y, z.
6. Скалярное
произведение векторов. Скалярное
произведение векторов определяется
как произведение модулей перемножаемых
векторов и косинуса угла между ними:
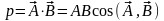 .
Обозначение скалярного произведения
обычно могут быть следующими:
.
Обозначение скалярного произведения
обычно могут быть следующими:
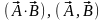 .
В последние годы в научных статьях стало
часто использоваться обозначение
.
В последние годы в научных статьях стало
часто использоваться обозначение
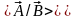 .
В этом курсе лекций при обозначении
скалярного произведения будет
использоваться точка.
.
В этом курсе лекций при обозначении
скалярного произведения будет
использоваться точка.
При
представлении векторов по компонентам
скалярное произведение будет равно
следующей сумме
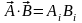 (i =x,
y, z).
Напомним, что при написании этой формулы
использовано соглашение о суммировании.
(i =x,
y, z).
Напомним, что при написании этой формулы
использовано соглашение о суммировании.
Свойства скалярного произведения:
К)
коммутативность:
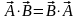 ;
;
А)
ассоциативность:
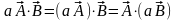 ;
;
Д)
дистрибутивность:
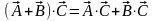 .
.
Следствия:
1)
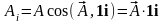 ;
;
2)
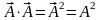 ,
,
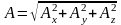 ,
,
3)
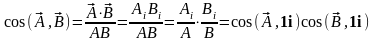 ;
;
4)
условие ортогональности векторов –
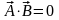 .
.
7 .
Векторное произведение векторов.
Векторное произведение двух векторов
определяет вектор ортогональный исходным
векторам и образующий с ними правую
тройку. Модуль нового вектора равен
произведению модулей перемножаемых
векторов и синуса угла между ними, т.е.
площади параллелограмма, построенного
на перемножаемых векторах:
.
Векторное произведение векторов.
Векторное произведение двух векторов
определяет вектор ортогональный исходным
векторам и образующий с ними правую
тройку. Модуль нового вектора равен
произведению модулей перемножаемых
векторов и синуса угла между ними, т.е.
площади параллелограмма, построенного
на перемножаемых векторах:
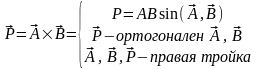
Векторное
произведение может так же обозначаться
следующими записями:
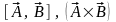 .
В нашем курсе лекций векторное произведение
будет обозначаться знаком умножения.
.
В нашем курсе лекций векторное произведение
будет обозначаться знаком умножения.
Векторное произведение можно записать через компоненты с помощью определителя:
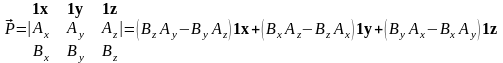 .
.
Свойства векторного произведения:
АК)
антикоммутативность:
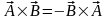 ;
;
А)
ассоциативность:
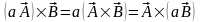 ;
;
Д)
дистрибутивность:
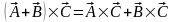 .
.
Основные
следствия: 1)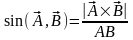 ,
,
2)
признак коллинеарности двух векторов
– их векторное произведение равно
0 (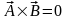 ).
).
8. Смешанное
произведение векторов определяется
выражением
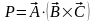 .
Значение величины P
равно объему параллелепипеда, построенного
на векторах
,
.
Значение величины P
равно объему параллелепипеда, построенного
на векторах
,
 и
и
 ,
и это значение положительно (+), если
вектора образуют правую тройку, и
отрицательно – если левую. Покомпонентная
запись смешанного произведения может
быть представлена следующим определителем:
,
и это значение положительно (+), если
вектора образуют правую тройку, и
отрицательно – если левую. Покомпонентная
запись смешанного произведения может
быть представлена следующим определителем:
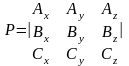 .
.
С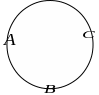 войства
смешанного произведения:
войства
смешанного произведения:
1) Инвариантность по отношению к циклической перестановке:
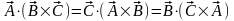 ,
,
и, как следствие, инвариантность по отношению к последовательности операций:
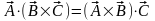 .
.
В
силу этого свойства смешанное произведение
часто обозначают выражением
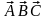 .
.
2)
Дистрибутивность:
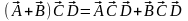 .
.
3)
Ассоциативность:
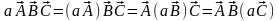 .
.
Основное
следствие: признак компланарности
векторов – их смешанное произведение
равно нулю (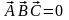 ).
).
9. Двойное
векторное произведение:
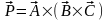 .
Можно показать, что двойное векторное
произведение может быть представлено
следующим выражением:
.
Можно показать, что двойное векторное
произведение может быть представлено
следующим выражением:
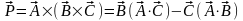 .
.
Вектор
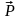 компланарен векторам
и
.
компланарен векторам
и
.
Свойства двойного векторного произведения:
Д)
Дистрибутивность:
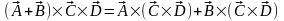 .
.
А)
Ассоциативность:
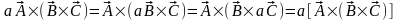 .
.
10. Матрицы. Совокупность чисел иногда удобно представлять в виде таблиц, называемых матрицами:
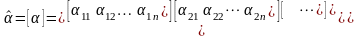 .
.
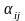 – элемент
матрицы, i – номер
строки, j – номер
столбца.
– элемент
матрицы, i – номер
строки, j – номер
столбца.
Напомним,
что, если m = n,
то такая матрица – квадратная, и n
– порядок этой матрицы. Если все элементы
квадратной матрицы равны нулю за
исключением диагональных
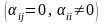 ,
то такая матрица носит название
диагональной. Если к тому же все
диагональные элементы диагональной
матрицы равны единице (
,
то такая матрица носит название
диагональной. Если к тому же все
диагональные элементы диагональной
матрицы равны единице (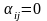 при i≠j,
и
при i=j),
то такая матрица называется единичной
и обозначается буквой Е.
при i≠j,
и
при i=j),
то такая матрица называется единичной
и обозначается буквой Е.
Матрица
называется транспонированной
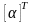 ,
если элементы строк этой матрицы
образованы из столбцов матрицы
,
если элементы строк этой матрицы
образованы из столбцов матрицы
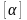 ,
т.е.
,
т.е.
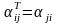 .
.
Сложение
матриц
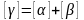 возможно только тогда, когда размерности
складываемых матриц совпадают. Элементы
результативной матрицы определяются
через элементы слагаемых матриц –
возможно только тогда, когда размерности
складываемых матриц совпадают. Элементы
результативной матрицы определяются
через элементы слагаемых матриц –
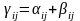 .
Для сложения матриц справедливо свойство
коммутативности и ассоциативности.
.
Для сложения матриц справедливо свойство
коммутативности и ассоциативности.
Умножение
матрицы на число
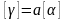 – все элементы исходной матрицы
умножаются на заданное число –
– все элементы исходной матрицы
умножаются на заданное число –
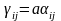 .
Для умножения матрицы на число и сложения
матриц справедливо свойство
дистрибутивности.
.
Для умножения матрицы на число и сложения
матриц справедливо свойство
дистрибутивности.
П роизведение
матриц
роизведение
матриц
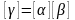 существует, если число столбцов первой
матрицы
равно числу строк второй матрицы
существует, если число столбцов первой
матрицы
равно числу строк второй матрицы
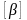 .
Элементы результативной матрицы
определяются по правилу
.
Элементы результативной матрицы
определяются по правилу
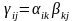 ,
где k = 1, …, n. (2.1)
,
где k = 1, …, n. (2.1)
Вектор
в матричной форме можно представить
как столбец
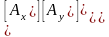 или как строку
или как строку
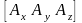 .
Такие представления вектора носят
соответствующие названия вектора-столбца
и вектора-строки. Скалярное произведение
векторов с помощью матриц можно
представить в виде:
.
Такие представления вектора носят
соответствующие названия вектора-столбца
и вектора-строки. Скалярное произведение
векторов с помощью матриц можно
представить в виде:
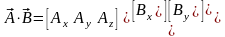 .
.
Матрица
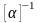 называется обратной к матрице
,
если их произведение равно матрице E:
называется обратной к матрице
,
если их произведение равно матрице E:
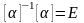 .
.
11. Переход от старого базиса к новому.
При решении ряда задач может возникнуть желание или необходимость ввода новой системы координат, в которой, на пример, будет проще производить расчеты или выкладки. Однако, в этом случае, координаты положения точки в новой системе координат будут отличными от координат той же точки в старой системе. Направления векторов, а соответственно и их компоненты, также будут зависеть от системы отсчета. Возникает вопрос, каким образом будут связаны компоненты вектора или координаты положения точки в этих системах отсчета?
Для
ответа на этот вопрос рассмотрим два
базиса: исходный декартовый базис
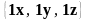 и новый базис
и новый базис
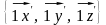 ,
образованный разворотом исходного
базиса. Разложим орт
,
образованный разворотом исходного
базиса. Разложим орт
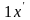 нового
базиса по старому:
нового
базиса по старому:
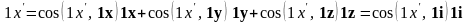
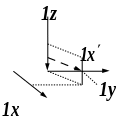 ,
(i = x,
y, z).
,
(i = x,
y, z).
В более краткой форме это выражение можно записать:
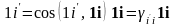 ,
,
где
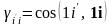 .
.
Аналогичным
образом можно представить орты
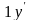 и
и
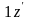 через орты старого базиса.
через орты старого базиса.
Полученные соотношения могут быть представлены в матричной форме:
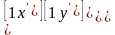 или
. (2.3)
или
. (2.3)
Осуществив разложение ортов базиса по ортам нового базиса , получим формулу перехода от нового базиса к старому:
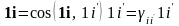 ,
(i = x,
y, z),
,
(i = x,
y, z),
или в матричной форме:
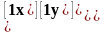 ;
. (2.3)
;
. (2.3)
Здесь
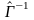 обозначает матрицу (оператор) обратного
перехода от нового базиса к старому.
Эта матрица (оператор) будет обратный
к матрице (оператору)
обозначает матрицу (оператор) обратного
перехода от нового базиса к старому.
Эта матрица (оператор) будет обратный
к матрице (оператору)
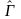 ,
т.е.
,
т.е.
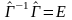 .
.
Отметим,
что в данном случае обратная матрица
равна транспонированной матрице
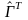 .
Однако стоит обратить внимание, что это
частный случай, а в большинстве случаев
обратная матрица не совпадает с
транспонированной. В курсе линейной
алгебры рассматриваются специальные
методы построения обратных матриц
(операторов).
.
Однако стоит обратить внимание, что это
частный случай, а в большинстве случаев
обратная матрица не совпадает с
транспонированной. В курсе линейной
алгебры рассматриваются специальные
методы построения обратных матриц
(операторов).
12. Преобразование компонент вектора при смене базисов.
Рассмотрим вектор . Этот вектор можно разложить по базису как старой, так и новой системы координат:
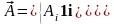 , где
i = x,
y, z.
, где
i = x,
y, z.
Поскольку
нами раскладывался один и тот же вектор
,
то
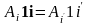 :
:
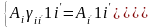 .
.
Поскольку
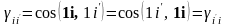 ,
то для компонент вектора можно записать:
,
то для компонент вектора можно записать:
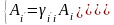 .
.
Полученные соотношения для преобразования компонент вектора при переходе от одной системы координат к другой носят название векторного закона преобразования. Отсюда, в частности, следует, что не любые три числа являются компонентами вектора. Вектором называется совокупность трех чисел, которые при смене базиса преобразуются по векторному закону. Отметим, что неизменным при смене базиса остается его модуль, эта величина является инвариантом вектора (параметром, не зависящим от системы отсчета).
Как пример, рассмотрим ситуацию, когда в каждой точке некоторой области пространства измеряется плотность вещества, его температура и давление. И хотя эти три числа формально можно записать как “вектор”, но вектор они образовывать не будут, поскольку при переходе от одной системы координат к другой их значения не будут преобразовываться согласно векторному закону.
В матричной форме векторный закон преобразования компонент вектора может быть представлен в виде:
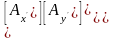 ;
.
;
.
13. Понятие тензора.
Рассмотрим
линейные соотношения между векторами.
Как пример частного случая таких
соотношений можно привести Закон Ома
в дифференциальной форме
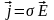 .
Согласно этому закону плотность
электрического тока в среде прямо
пропорциональна напряженности
электрического поля и совпадает с ним
по направлению. Коэффициентом
пропорциональности служит значение
электропроводности среды. Однако
возможна такая ситуация, когда
электропроводность среды будет меняться
в зависимости от направления, т.е. в
одном направлении эта величина может
быть большой, а в каком-то другом –
маленькой. В этом случае Закон Ома будет
более сложным, и в том виде, как он был
записан выше, не будет верен.
.
Согласно этому закону плотность
электрического тока в среде прямо
пропорциональна напряженности
электрического поля и совпадает с ним
по направлению. Коэффициентом
пропорциональности служит значение
электропроводности среды. Однако
возможна такая ситуация, когда
электропроводность среды будет меняться
в зависимости от направления, т.е. в
одном направлении эта величина может
быть большой, а в каком-то другом –
маленькой. В этом случае Закон Ома будет
более сложным, и в том виде, как он был
записан выше, не будет верен.
Линейной
векторной функцией векторного аргумента
называется функция
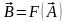 ,
которая удовлетворяет свойствам: 1)
аддитивности -
,
которая удовлетворяет свойствам: 1)
аддитивности -
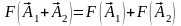 ;
;
2)
однородности -
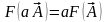 .
.
Связь между компонентами векторов и в этом случае может быть получена в результате следующих преобразований:
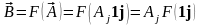 .
.
Обозначим
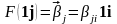 .
Тогда:
.
Тогда:
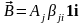 ;
; 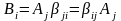 ,
где i, j
= x, y,
z.
,
где i, j
= x, y,
z.
Таким образом, компоненты вектора преобразуются в компоненты вектора с помощью матрицы:
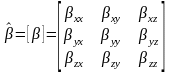 .
.
Объект
 носит название тензора, а элементы
носит название тензора, а элементы
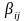 - компоненты тензора. Тензор осуществляет
линейное преобразование вектора
в вектор
.
- компоненты тензора. Тензор осуществляет
линейное преобразование вектора
в вектор
.
Определение. Тензор – физический объект, определяемый совокупностью чисел. При переходе от одной координатной системы к другой эти числа преобразуются по правилам, обеспечивающим инвариантность объекта. Тензор – совокупность чисел, каждое из которых связано с координатными осями. Число связей существующих между каждой компонентой тензора и координатными осями определяют валентность тензора.
Скалярная величина – тензор нулевой валентности.
Векторная величина – тензор первой валентности. При переходе от одной координатной системы к другой компоненты вектора преобразуются согласно закону векторного преобразования.
Построенная матрица носит название тензора второй валентности, аффинора и просто тензора. При смене базиса компоненты тензора преобразуются по закону
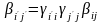 .
.
Лекция III. Дифференцирование физических полей.
Физические
поля могут быть скалярными
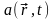 и векторными
и векторными
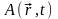 .
Дифференцирование таких полей
осуществляется как по пространственным
координатам, так и по времени. В том
случае, если производная по времени от
таких полей равна нулю(
.
Дифференцирование таких полей
осуществляется как по пространственным
координатам, так и по времени. В том
случае, если производная по времени от
таких полей равна нулю(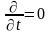 ),
то такие поля – стационарные. В той
записи, которой мы использовали,
координата точки, в которой рассматривается
поле, определяется радиусом-вектором
),
то такие поля – стационарные. В той
записи, которой мы использовали,
координата точки, в которой рассматривается
поле, определяется радиусом-вектором
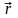 .
В декартовых координатах радиус-вектор
можно представить в виде:
.
В декартовых координатах радиус-вектор
можно представить в виде:
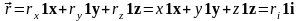 .
.
1. Дифференцирование
скалярного поля
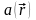 .
.
При
дифференцировании скалярного поля
можно вычислить три частные производные
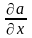 ,
,
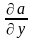 ,
,
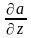 .
Покажем, что эти три частные производные
образуют вектор. Для этого надо доказать,
что при смене базиса значения этих
производных преобразуются по векторному
закону. Рассмотрим радиус-вектор
.
В старом и новом базисе этот вектор
можно представить через его компоненты:
.
Покажем, что эти три частные производные
образуют вектор. Для этого надо доказать,
что при смене базиса значения этих
производных преобразуются по векторному
закону. Рассмотрим радиус-вектор
.
В старом и новом базисе этот вектор
можно представить через его компоненты:
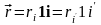 .
.
Тогда,
частная производная по координате
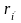 будет
определяться соотношением:
будет
определяться соотношением:
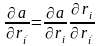 ,
где i = x,
y, z.
,
где i = x,
y, z.
Пример: 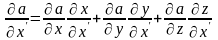 .
.
Вспомним,
о том, что для вектора
справедливо соотношение
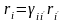 .
Тогда
.
Тогда
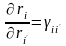 и, соответственно,
и, соответственно,
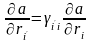 .
Тем самым мы показали, что частные
производные при смене базиса преобразуются
по векторному закону. Это означает, что
из частных производных может быть
образован вектор – градиент скалярного
поля:
.
Тем самым мы показали, что частные
производные при смене базиса преобразуются
по векторному закону. Это означает, что
из частных производных может быть
образован вектор – градиент скалярного
поля:
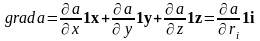 , где
i = x,
y, z. (3.1)
, где
i = x,
y, z. (3.1)
Результат. Со скалярным полем инвариантно связано векторное поле его градиента.
2. Производная скалярного поля по направлению.
Рассмотрим
изменение скалярного поля
 вдоль некоторой прямой, направление
которой характеризуется вектором
вдоль некоторой прямой, направление
которой характеризуется вектором
 .
Тогда в точке M, лежащей
на этой прямой значение поле будет равно
a, а в точке M,
находящейся на этой же прямой на
расстоянии l,
значение поля изменится на некоторую
величину a
и будет равно
.
Тогда в точке M, лежащей
на этой прямой значение поле будет равно
a, а в точке M,
находящейся на этой же прямой на
расстоянии l,
значение поля изменится на некоторую
величину a
и будет равно
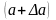 .
Тогда, изменение поля на участке l
можно охарактеризовать отношением
.
Тогда, изменение поля на участке l
можно охарактеризовать отношением
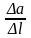 .
При l,
стремящемся к нулю, это отношение будет
равно производной поля a
по направлению
:
.
При l,
стремящемся к нулю, это отношение будет
равно производной поля a
по направлению
:
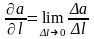
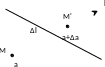 .
.
Дифференциал скалярного поля по направлению 1l соответственно определяется соотношением:
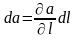 .
.
Для производной и дифференциала поля a по направлению 1l можно записать:
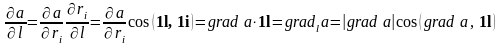 , (3.2)
, (3.2)
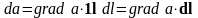 . (3.3)
. (3.3)
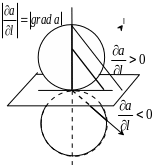 Рассмотрим
физический смысл производной скалярного
поля по направлению. Для этого обратим
внимание на то, что максимального
значения производная достигает в том
случае, когда
Рассмотрим
физический смысл производной скалярного
поля по направлению. Для этого обратим
внимание на то, что максимального
значения производная достигает в том
случае, когда
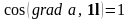 .
В этом случае направление градиента
поля a и направления
1l совпадают,
и значение производной будет равно
значению градиента:
.
В этом случае направление градиента
поля a и направления
1l совпадают,
и значение производной будет равно
значению градиента:
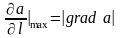 .
.
Отсюда
следует, что градиент имеет направление
быстрейшего увеличения поля a
и равен производной
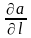 по этому направлению, и что градиент
характеризует поведение скалярного
поля в окрестности точки наблюдения.
Он определяет скорость изменения поля
по любому лучу из точки наблюдения, т.е.
по любому направлению.
по этому направлению, и что градиент
характеризует поведение скалярного
поля в окрестности точки наблюдения.
Он определяет скорость изменения поля
по любому лучу из точки наблюдения, т.е.
по любому направлению.
3. Оператор Гамильтона.
Оператор – символ, указывающий каким операциям надо подвергнуть величину, стоящую после оператора.
Введем линейный векторный оператор
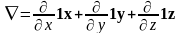 =
=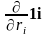 . (3.4)
. (3.4)
Этот оператор носит название “набла” или “оператор Гамильтона”. С его помощью операцию вычисления градиента можно представить в следующем виде:
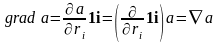 .
.
Соответственно,
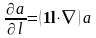 =
=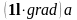 ,
, 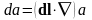 =
=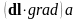 .
.
Алгебра
с оператором Гамильтона
почти совпадает с векторной алгеброй,
но необходимо помнить, что этот оператор
в первую очередь оператор дифференцирования,
и что для него нельзя пользоваться
правилом коммутативности. Так, если для
скалярной величины a
и векторного поля
соотношение
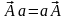 справедливо, то для оператора
это не так:
справедливо, то для оператора
это не так:
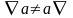 ,
и при этом запись
,
и при этом запись
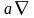 лишена всякого смысла.
лишена всякого смысла.
4. Дифференцирование векторного поля.
Рассмотрим
векторное поле
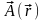 .
В декартовом базисе это поле имеет
компоненты
.
В декартовом базисе это поле имеет
компоненты
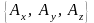 .
Каждая из этих компонент может меняться
в пространстве, и их изменение в
окрестности точки наблюдения может
характеризоваться следующей совокупностью
частных производных:
.
Каждая из этих компонент может меняться
в пространстве, и их изменение в
окрестности точки наблюдения может
характеризоваться следующей совокупностью
частных производных:
 .
.
А налогично
тому, как мы определили производную
скалярного поля по направлению, определим
производную векторного поля
по направлению 1l.
Для этого рассмотрим точки M
и M,
лежащие на прямой на расстоянии l
друг от друга. Значение поля
в точке M
изменится на величину
налогично
тому, как мы определили производную
скалярного поля по направлению, определим
производную векторного поля
по направлению 1l.
Для этого рассмотрим точки M
и M,
лежащие на прямой на расстоянии l
друг от друга. Значение поля
в точке M
изменится на величину
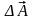 по сравнению с точкой M.
Тогда
по сравнению с точкой M.
Тогда
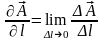 .
.
Дифференциал векторного поля по направлению будет определяться соотношением
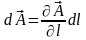 .
.
С помощью операции вычисления градиента и оператора Гамильтона производную и дифференциал по направлению векторного поля можно представить в виде:
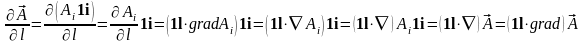 ,(3.5)
,(3.5)
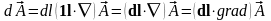 . (3.6)
. (3.6)
Последнее соотношение носит название градиента вектора по вектору dl. Это соотношение можно обобщить и вместо вектора dl взять любой вектор , т.е. определить градиент вектора по вектору :
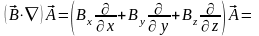
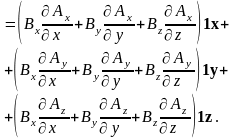
5. Дивергенция и ротор векторного поля.
Как будет показано в дальнейшем, поле можно определить с помощью следующих двух инвариантов – дивергенции и ротора, которые пока введем формально:
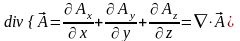 ,
(3.7)
,
(3.7)
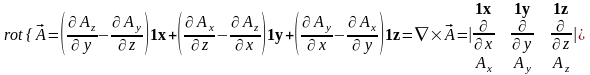 . (3.8)
. (3.8)
Замечание. В зарубежной литературе вместо обозначения rot может встречаться обозначение curl.
6. Основные дифференциальные операции.
Дифференциальные операции grad, div, rot – пространственные производные поля. Эти операции дифференцирования подчиняются основным правилам дифференцирования:
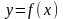 ,
,
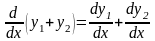 ,
,
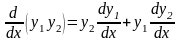 ,
,
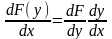 .
.
При вычислении производных оператор Гамильтона должен занять надлежащее место.
7. Первые производные скалярных и векторных полей.
Градиент скалярного поля.
1. 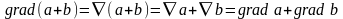 ;
(3.9)
;
(3.9)
2. 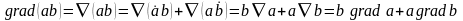 ;
(3.10)
;
(3.10)
3. 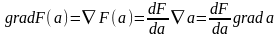 ;
(3.11)
;
(3.11)
4. 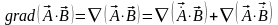 ;
;
Рассмотрим первое слагаемое:
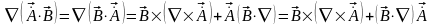 .
.
Аналогичным образом можно представить и второе слагаемое. В результате:
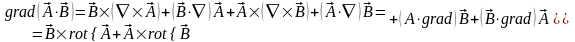 (3.12)
(3.12)
Дивергенция.
5. 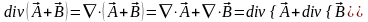 ;
(3.13)
;
(3.13)
6. 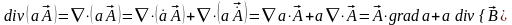 ;
(3.14)
;
(3.14)
7. 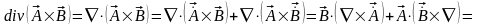
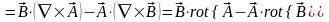 ; (3.15)
; (3.15)
Ротор.
8. 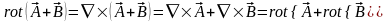 ;
(3.16)
;
(3.16)
9.  ;
(3.17)
;
(3.17)
10. 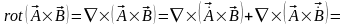
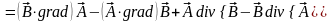 .
(3.18)
.
(3.18)
8. Вторые производные полей.
Физическое поле может быть скалярным a или векторным . Рассмотрим возможные ситуации:
-
a
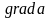
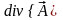
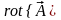
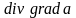
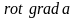
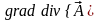
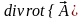
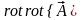
1. 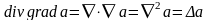 .
(3.19)
.
(3.19)
Здесь введен новый оператор – оператор Лапласа или лапласиан:
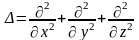 . (3.20)
. (3.20)
2. 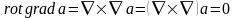 .
(3.21)
.
(3.21)
3. 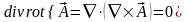 .
(3.22)
.
(3.22)
4. 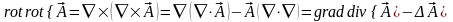 .
(3.23)
.
(3.23)
Из последнего соотношения получим определение лапласиана векторной функции:
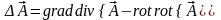 . (3.24)
. (3.24)
Следует отметить, что для декартового базиса справедливо следующее представление:
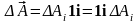 ,
где i = x,
y, z,
,
где i = x,
y, z,
Однако, в криволинейных системах координат, о которых будем говорить в следующих лекциях, такая запись не верна.
В
заключении этой лекции обратим еще раз
внимание на коварство аналогии оператора
Гамильтона с вектором. Так для вектора
справедлива запись
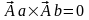 ,
в то же время
,
в то же время
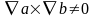 .
Еще один пример -
.
Еще один пример -
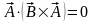 ,
,
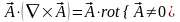 .
Более правильно было бы сказать, что
иногда возможны ситуации, когда
.
Более правильно было бы сказать, что
иногда возможны ситуации, когда
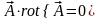 ,
но в общем случае, это не так. Достаточно
легко придумать примеры, подтверждающие
справедливость последнего соотношения.
А вот предположение о том, что
может привести к неверным выводам. Для
этого рассмотрим второе уравнение
Максвелла
,
но в общем случае, это не так. Достаточно
легко придумать примеры, подтверждающие
справедливость последнего соотношения.
А вот предположение о том, что
может привести к неверным выводам. Для
этого рассмотрим второе уравнение
Максвелла
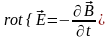 .
.
Умножим
скалярно обе части этого уравнения на
вектор
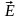 :
:
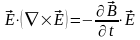 .
.
Предположение о том, что выражение в правой части уравнения всегда равно нулю, приводит к выводу о том, поле всегда ортогонально полю . Этот неверный вывод утверждается в учебнике И.К. Овчиникова «Теория поля».
Лекция IV. Интегрирование физических полей.
В этой лекции будем говорить об интегрировании скалярных и векторных стационарных полей, т.е. полей не зависящих от времени. Условие стационарности – .
1. Типы интегралов.
Интегралы могут быть объемными, поверхностными и криволинейными.
Объемные интегралы:
скалярное
поле – 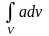 ;
;
векторное
поле – 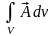 .
.
В декартовом базисе объемный интеграл от векторного поля можно представить в виде:
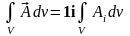 , i
= x, y,
z.
, i
= x, y,
z.
2. Поверхностные интегралы.
Поверхностные
интегралы могут быть первого и второго
рода. Напомним, что в поверхностный
интеграл первого рода вводится, как
предел интегральной суммы
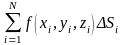 при
при
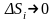 .
Если такой предел существует и равен
I, то I
называется поверхностным интегралом
1-го рода от функции
.
Если такой предел существует и равен
I, то I
называется поверхностным интегралом
1-го рода от функции
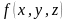 по поверхности S и
обозначается
по поверхности S и
обозначается
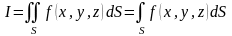 .
.
 Для
определения интеграла второго рода
необходимо ввести понятие ориентации
двусторонней поверхности. Для этого
вводится понятие вектор-площадки
Для
определения интеграла второго рода
необходимо ввести понятие ориентации
двусторонней поверхности. Для этого
вводится понятие вектор-площадки
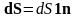 .
Здесь 1n –
единичный вектор, ортогональный к
площадке dS, и его
направление определяется следующим
образом. Если поверхность замкнута, то
вектор 1n
направлен от ее внутренней стороны к
внешней. Если поверхность не замкнута,
то направление нормали определяется
направлением обхода контура L,
ограничивающего эту поверхность, и это
направление определяется по правилу
правого винта.
.
Здесь 1n –
единичный вектор, ортогональный к
площадке dS, и его
направление определяется следующим
образом. Если поверхность замкнута, то
вектор 1n
направлен от ее внутренней стороны к
внешней. Если поверхность не замкнута,
то направление нормали определяется
направлением обхода контура L,
ограничивающего эту поверхность, и это
направление определяется по правилу
правого винта.
В отличие от интегралов 1-го рода, в которых интегрирование осуществляется по площади элементарной площадки, в интегралах 2-го рода интегрирование осуществляется по проекции элементарной площадки на координатные поверхности. Если проекции элементарной площадки на координатные плоскости однозначны, то можно определить следующие поверхностные интегралы 2-го рода от функции :
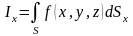 ,
,
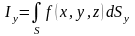 ,
,
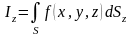 .
.
Знак интегралов определяется направлением вектора нормали. Если вектор нормали образует с координатной осью острый угол, то знак интеграла – положительный, а если тупой – то знак отрицательный. Эти интегралы можно объединить в один:
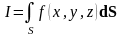 .
.
В дальнейшем нами будут рассматриваться только интегралы 2-го рода.
Классификация интегралов:
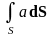 –
поток скалярного поля через поверхность
S;
–
поток скалярного поля через поверхность
S;
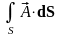 – скалярный поток векторного поля через
поверхность S;
– скалярный поток векторного поля через
поверхность S;
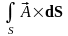 – векторный поток векторного поля через
поверхность S;
– векторный поток векторного поля через
поверхность S;
Интегрирование
через замкнутую поверхность обозначается
значком
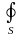 .
.
3. Криволинейные интегралы.
Как
и поверхностные интегралы, криволинейные
интегралы могут быть первого и второго
рода. Аналогично поверхностным интегралам
в криволинейных интегралах 1-го рода
интегрирование осуществляется по длине
дуги dl, а в криволинейных
интегралах 2-го рода интегрирование
осуществляется по проекциям элемента
дуги dl на координатные
оси. Аналогично тому, как было введено
понятие вектор-площадки, мы можем
определить вектор
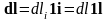 ,
где
,
где
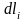 – проекции элемента dl
на координатные оси, 1l
– единичный вектор, совпадающий с
касательной к контуру и направленный
по направлению обхода.
– проекции элемента dl
на координатные оси, 1l
– единичный вектор, совпадающий с
касательной к контуру и направленный
по направлению обхода.
Классификация интегралов:
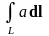 ;
;
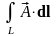 – напряжение
векторного поля на пути L;
– напряжение
векторного поля на пути L;
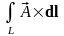 ;
;
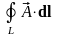 – циркуляция
вектора
.
– циркуляция
вектора
.
Основные интегральные соотношения.
4. Теорема Гаусса – Остроградского.
Пусть
функции P, Q,
R и их частные
производные
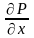 ,
,
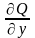 ,
,
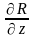 непрерывны внутри области V
и на замкнутой поверхности S,
ограничивающей этот объем. Тогда
справедливо
непрерывны внутри области V
и на замкнутой поверхности S,
ограничивающей этот объем. Тогда
справедливо
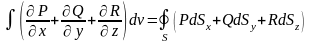 .
.
Это соотношение распространяется и на векторные поля.
Векторные формулировки теоремы Остроградского – Гаусса.
А) Пусть
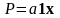 ,
,
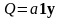 ,
,
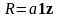 .
Тогда:
.
Тогда:
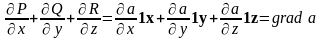 ;
;
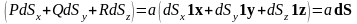 ;
;
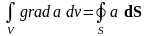 . (4.1)
. (4.1)
Б) Рассмотрим
вектор
,
и пусть
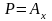 ,
,
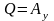 ,
,
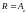 :
:
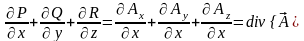 ;
;
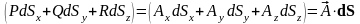 ;
;
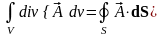 . (4.2)
. (4.2)
В) Осуществим следующие преобразования:
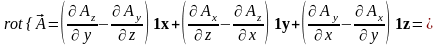
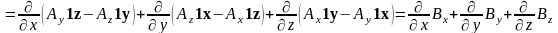 ;
;
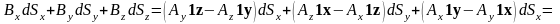
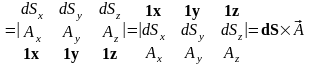 ;
;
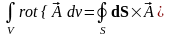 . (4.3)
. (4.3)
На основании полученных соотношений можно определить следующие объемные производные:
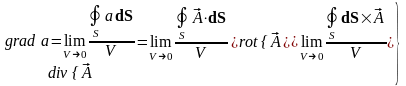 . (4.4)
. (4.4)
5. Теорема Стокса.
Пусть
функции P, Q,
R и их частные производные
,
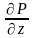 ,
,
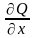 ,
,
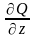 ,
,
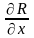 ,
непрерывны на поверхности S
и на замкнутом контуре L,
ограничивающем эту поверхность. Тогда
,
непрерывны на поверхности S
и на замкнутом контуре L,
ограничивающем эту поверхность. Тогда
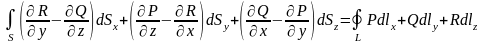 .
.
Векторные формулировки теоремы Стокса.
А) Пусть , , . Тогда
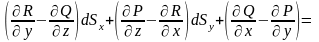
=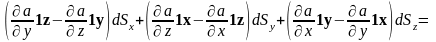
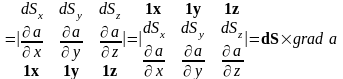 ;
;
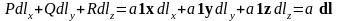 ;
;
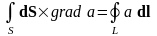 . (4.5)
. (4.5)
Б) Пусть
,
,
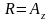 ,
где
,
где
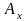 ,
,
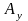 ,
,
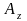 – компоненты вектора
.
Тогда теорема Стокса приобретет запись:
– компоненты вектора
.
Тогда теорема Стокса приобретет запись:
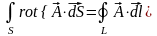 . (4.6)
. (4.6)
В
качестве упражнения покажем, как из
уравнения (4.6) можно получить уравнение
(4.5). Для этого положим, что
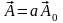 ,
где
,
где
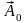 - некоторый ненулевой вектор. Далее:
- некоторый ненулевой вектор. Далее:
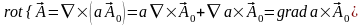 ,
,
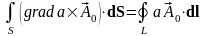 ,
,
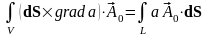 ,
,
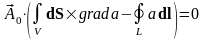 ,
,
т.к. - ненулевой вектор, то
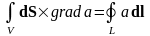 .
.
Используя последнюю формулировку теоремы (4.6), можем определить следующую производную:
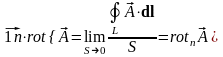 . (4.7)
. (4.7)
