Задание 2.

2.1. Над полем GF(2) методом Гаусса найти определитель матрицы А размера n x n, состоящей из младших разрядов двоичного разложения числа abс, сдвинутого циклически.

abc = 101111010

А =

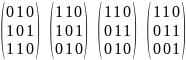
|A| = 1 * 1 * 1 = 1

2.2. Методом Гаусса найти характеристический многочлен матрицы А.

Характеристический многочлен f(λ):

f(λ) = |A - λE| = 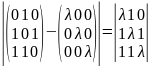= λ³ + 0 + 1 – 0 – λ – λ = λ³ + 1

2.3. Разложить многочлен f(λ) над полем GF(2) на неприводимые множители и найти его корни.

f(λ) = λ³ + 1 = (λ² + λ + 1)( λ + 1)

λ² + λ + 1 = 0 – корней не имеет

λ + 1 = 0

λ = 1

Ответ: 1.

2.4. Найти собственные вектора для всех собственных значений матрицы А.

А =

Определим координаты собственного вектора:

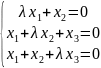
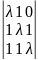= λ³ + 1

Находим корни:

λ³+1=0

λ = 1

Подставляем в систему:

Ранг матрицы системы линейных уравнений = 2, следовательно, зависимых переменных две, свободная одна.

Пусть 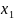– свободная переменная, тогда:

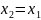
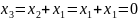
Ф.С.Р:

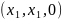
Таким образом, все собственные векторы матрицы А:

(1, 1, 0), (0, 0, 0)

2.5. Разложить на неприводимые множители над полем GF(2) многочлен f(x).

?задание разложить многочлен есть, а самого многочлена в задании нет

2.6. Найти элемент, обратный по умножению к элементу 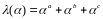в поле GF(2⁷).

λ(α) = α⁷ + α⁶ + α⁹

Построим поле, используя элемент α⁷ + α³ + 1

f(x) = x⁷ + x³ + 1

f(x) ≠ 0

f(α) = 0

α⁷ + α³ + 1 = 0

α⁷ = α³ + 1

α⁸ = α⁴ + α

α⁹ = α⁵ + α²

α¹⁰ = α⁶ + α³

α¹¹ = α⁴ + α³ + 1

Элемент, которому ищем обратный, будет иметь вид:

λ(α) = α⁷ + α⁶ + α⁹ = α⁶ + α⁵ + α³ + α² + 1

Найдем обратный, используя алгоритм Евклида:

f(α) = (α + 1) * λ(α) + (α⁵ + α⁴ + α³ + α² + α)

λ(α) = α * (α⁵ + α⁴ + α³ + α² + α) + (α⁴ + 1)

(α⁵ + α⁴ + α³ + α² + α) = (α + 1) * (α⁴ + 1) + (α³ + α² + 1)

(α⁴ + 1) = (α + 1) * (α³ + α² + 1) + (α² + α)

(α³ + α² + 1) = α * (α² + α) + 1

1 = (α³ + α² + 1) + α * (α² + α)

1 = (α³ + α² + 1) + α * (α² + α) = (α³ + α² + 1) + α * [(α⁴ + 1) + (α + 1) * (α³ + α² + 1)] = = α * (α⁴ + 1) + (α² + α + 1) * (α³ + α² + 1) = α * (α⁴ + 1) + (α² + α + 1) * [(α⁵ + α⁴ + α³ + α² +

+ α) + (α + 1) * (α⁴ + 1)] = (α² + α + 1) * (α⁵ + α⁴ + α³ + α² + α) + (α³ + α + 1) * (α⁴ + 1) =

= (α² + α + 1) * (α⁵ + α⁴ + α³ + α² + α) + (α³ + α + 1) * [λ(α) + α * (α⁵ + α⁴ + α³ + α² + α)] =

= (α³ + α + 1) * λ(α) + (α⁴ + 1) * (α⁵ + α⁴ + α³ + α² + α) = (α³ + α + 1) * λ(α) + (α⁴ + 1) *

* [f(α) + (α + 1) * λ(α)] = (α⁴ + 1) * f(α) + (α⁵ + α⁴ + α³) * λ(α) = 0 + (α⁵ + α⁴ + α³) * λ(α) =

= (λ(α))^-1 * λ(α)

Обратный по умножению для α⁶ + α⁵ + α³ + α² + 1 будет α⁵ + α⁴ + α³

Проверка:

(α⁶ + α⁵ + α³ + α² + 1) * (α⁵ + α⁴ + α³) = α¹¹ + α¹⁰ + α⁸ + α⁷ + α⁵ + α¹⁰ + α⁹ + α⁷ + α⁶ +

+ α⁴ + α⁹ + α⁸ + α⁶ + α⁵ + α³ = α¹¹ + α⁴ + α³ = α⁴ + α³ + 1 + α⁴ + α³ = 1

Проверка показала, что найденный элемент является искомым

2.7. Найти порядок элемента λ(α).

α⁷ = α³ + 1

α⁸ = α⁴ + α

α⁹ = α⁵ + α²

α¹⁰ = α⁶ + α³

α¹¹ = α⁴ + α³ + 1

α¹² = α⁵ + α⁴ + α

α²⁰ = (α⁶ + α³) * (α⁶ + α³) = α¹² + α⁹ + α⁹ + α⁶ = α⁶ + α⁵ + α⁴ + α

α²¹ = α²⁰ * α = (α⁶ + α⁵ + α⁴ + α) * α = α⁷ + α⁶ + α⁵ + α² = α³ + 1 + α⁶ + α⁵ + α² =

= α⁶ + α⁵ + α³ + α² + 1

λ(α) = α²¹

2.8. Найти в какой степени элемент α^с станет равным элементу α

α^с = α⁹

(α⁹)² = α⁶ + α⁴ + α³

(α⁹)⁴ = α⁶ + α⁵

(α⁹)⁸ = (α⁹)⁴ * (α⁹)⁴ = α⁶ + α⁵ + α⁴ + α³ + α

(α⁹)¹⁶ = (α⁹)⁸ * (α⁹)⁸ = α⁵ + α³ + α²

(α⁹)³² = (α⁹)¹⁶ * (α⁹)¹⁶ = α⁴ + α³

(α⁹)⁶⁴ = (α⁹)³² * (α⁹)³² = α⁶ + α⁴ + 1

(α⁹)⁹⁶ = (α⁹)⁶⁴ * (α⁹)³² = α⁶ + α² + α + 1

(α⁹)¹¹² = (α⁹)⁹⁶ * (α⁹)¹⁶ = α⁶ + α⁵ + α

(α⁹)¹¹³ = (α⁹)¹¹² * α⁹ = α

(α⁹)¹¹³ = α

Ответ: в 113 степени.