2. Основные понятия. Операция – совокупность действий, направленных на достижение поставленной цели; управляемое мероприятие. Наличие цели подразумевает существование активных участников, преследующих цель. Оперирующая сторона – группа лиц, стремящихся к поставленной цели. Исследователь операции – участник оперирующей стороны, преследующий цель оперирующей стороны, но не принимающий решений по выбору способов действий, а дает рекомендации, оперирующей стороне. Сложность – должен предусмотреть возможное поступление информации и дать рекомендации по правилам поведения с учетом этой информации. Оптимальное решение – решение, предпочтительное другим по каким-либо признакам. Цель исследователя операции заключается в предварительном обосновании оптимальных решений.

3. Математическая модель операции – основной инструмент исследования операций. Ресурсы, находящиеся в распоряжении оперирующей стороны, необходимые для достижения цели – активные средства. Действия, направленные на достижение поставленной цели представляют собой способы использования активных средств и называются стратегиями.

В зависимости от информированности исследователя операций о неконтролируемых факторах: 1) фиксируемые (факторы, значения которых точно известны исследователю операции); 2) случайные (случайная величина, закон распределения которой точно известен исследователю операций); 3) неопределенные (детерминируемые с. в., относительно которых исследователю операции известно лишь множество возможных значений или класс возможных законов распределения).

7. Различные типы задач исследования операций. 1) по неконтролируемым факторам: 1.1) задачи математического программирования; 1.2) задачи стохастического программирования; 1.3) задачи принятия решений в условиях неопределенности. 1.1.1)ЗЛП; 1.1.2) ЗНЛП. 1.2.1) Задачи массового обслуживания; 1.2.2) Задачи управления запасами; 1.2.3) Задачи надежности систем; 1.3.1) Принцип гарантированного результата; 1.3.2) Теория игр.

2) по подходам к решению: 2.1) прямые (что будет если в заданных условиях мы примем какое-то решение); 2.2) обратные (Как выбрать решение, чтобы критерий эффективности обратился в максимум).

8. Основные понятия т.и. Конфликт – операция в которой участвуют несколько сторон, по крайней мере 2, обладающие своими собственными целями. Математическую модель конфликтной ситуации называют игрой. Раздел исследования операций занимающийся математическими моделями принятия оптимальных решений в условии конфликта называется теорией игр. Основная её задача – разрешение конфликта, т. е. построение компромиссных взаимовыгодных решений. Целью теории игр является выработка рекомендаций для разумного поведения игроков в конфликтной ситуации, т. е. определение оптимальной стратегии каждого из них. Выбор всеми игроками определенных стратегий определяет исход или ситуацию игры.

9. Классификация игр. 1. Статические и динамические. 2. Принцип о допустимости образования коалиции: Если в игре образование коалиций недопустимо, то она называется бескоалиционной. Если в бескоалиционной игре множество допустимых ситуаций совпадает с прямым произведением пространств стратегий игроков и отношения предпочтения задаются с помощью функции выигрыша, то игра полностью задается множеством игроков, пространствами стратегий и функциями выигрыша. 3. Игры 2х лиц и игры n лиц. Если в бескоалиционной игре 2 участника и их интересы противоположны, то такая игра называется антагонистической. 4. В соответствии с формой задания игр: Позиционные и Игры в нормальной форме. 5. По числу возможных стратегий – Конечные и Бесконечные.

10. Если в бескоалиционной игре 2 участника и их интересы противоположны, то такая игра называется антагонистической. Оптимальной стратегией игрока в теории игр называется такая стратегия, которая при многократном проведении игры обеспечивает данному игроку максимально возможный средний выигрыш. Вероятностное распределение на множестве чистых стратегий называется смешанной стратегией. Множество смешанных стратегий является расширением множества чистых стратегий.

16. Принцип доминирования: Если i-ая строка матрицы игры доминируется некоторой линейной комбинацией остальных строк, то существует такая некоторая оптимальная стратегия Если j-ый столбец матрицы доминирует (строго) k-ый, то существует любая оптимальная стратегия

17. Преобразование матрицы выигрышей. 1. Вычеркивание строк и столбцов на основе принципа доминирования, при этом а расширения оптимальных стратегий дают оптимальные стратегии исходной игры. 2. Умножение матрицы на число , а множества оптимальных стратегий совпадают. 3. Увеличение элементов матрицы на одно и то же число: ; , а множества оптимальных стратегий совпадают. =>

21. Метод Шепли-Сноу позволяет находить полное решение. Множество оптимальных стратегий игроков являются выпуклыми многогранниками. А каждый многогранник определяется конечным числом своих крайних точек. Для нахождения полного решения достаточно определить некоторое множество оптимальных стратегий и взять выпуклую оболочку этих стратегий. Для решения матричной игры методом Шепли-Сноу: 1. Целесообразно, если возможно, уменьшить размерность матрицы. При этом если ищется полное решение, то вычеркивать можно только строго-доминируемые строки и столбцы. 2. В полученной матрице перебрать все квадратные подматрицы и для каждой из них решить соответствующую систему уравнений. При этом если 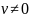система имеет единственное решение либо не имеет. 3. Из 2 шага => простой случай при условии невырожденности матрицы A, поэтому целесообразно свести исходную игру к игре с заведомо не равной ценой. 4. Полученные решения проверить на неотрицательность и на выполнение условий оптимальности: и на вычеркнутых столбцах и строках. 5. Найденное решение является оптимальным, но необязательно крайним, т. к. теорема дает необходимые условия крайности. Полный перебор всех квадратных подматриц игры приводит к нахождению множеств оптимальных стратегий игроков включающих в себя крайнюю. 6. Выпуклая оболочка, найденная методом Шепли-Сноу, множеств оптимальных стратегий дает нам множество всех оптимальных стратегий игроков.

27. Смешанное расширение.

] - смешанная стратегия i-ого игрока (вероятностное распределение на множестве чистых стратегий). ) – вероятность выбора j-ой стратегии i-ым игроком. - произвольная ситуация. . - определяет ситуацию в смешанных стратегиях. Ситуации в смешанных стратегиях реализуют различные ситуации в чистых стратегиях с некоторой вероятностью, поэтому значение функции выигрыша каждого из игроков оказывается случайной величиной ( в качестве значения функции выигрыша берут мат ожидание случайной величины). ; - смешанное расширение бескоалиционной игры n лиц. Ситуация называется ситуацией равновесия по Нэшу в смешанных стратегиях, если для каждого игрока и для каждой его смешанной стратегии выполняется . - множество номеров для которых вероятность выбора положительна – спектр смешанных стратегий p. Смешанная стратегия p, для которой называется вполне смешанной. Ситуация pq в которой обе стратегии вполне смешанны называется вполне смешанной.

29. Свойства оптимальных решений бескоалиционной игры.

1. Для биматричной игры если существует ситуация равновесия по Нэшу в смешанных стратегиях ; . Эта теорема дает способ нахождения равновесных стратегий . 2. Если в биматричной игре матрицы A и B невырожденные и игра имеет вполне смешанную ситуацию равновесия, то она единственная и вычисляется по формулам: U, W – единичные вектора. Обратно: Если для p и q, определяемых этими соотношениями выполняется условие не отрицательности, то они образуют ситуацию равновесия. 3. В каждой конечной бескоалиционной игре существует хотя бы одна ситуация равновесия по Нэшу в смешанных стратегиях. Замечание: т.к. чистая стратегия игрока является частным случаем смешанной стратегии вполне возможно, что биматричная игра имеет ситуацию равновесия по Нэшу в чистых стратегиях. Однако, если биматричная игра не имеет ни одной ситуации равновесия по Нэшу в чистых стратегиях согласно Th Нэша эта игра имеет хотя бы одну ситуацию равновесия по Нэшу в смешанных стратегиях.

30. Биматричные игры с малым числом стратегий.

; ] различны, - чистые стратегии 1ого игрока.

1. ] - строго доминирующая стратегия, тогда игра имеет одну ситуацию равновесия по Нэшу в чистых стратегиях . Тогда при - ситуация равновесия по Нэшу чистых стратегий или при . 2. Игра не имеет ситуаций равновесия по Нэшу в чистых стратегиях: 2.1. , 2.2. , т.к. ( - различны, то , , тогда согласно Th Нэша … 3. Игра имеет 2 ситуации равновесия по Нэшу в чистых стратегиях и или и . 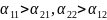, Однако и в смешанном расширении есть одна вполне смешанная ситуация равновесия по Нэшу, которые определяются по формулам случая 2.

31. Кооперативные игры.

Цель – суммировать выигрыш. Кооперативная игра – игра, в которой игрокам разрешается перед игрой обсуждать свои стратегии и договариваться о совместных действиях, образуя коалиции. ] N – {1,2,…,n} – множество игроков. Любое непустое подмножество множества игроков называется коалицией: . Характеристической функцией игры n лиц называют вещественную функцию V определенную на коалициях и удовлетворяющую условиям: ; . Свойство супер-аддитивности необходимо для содержательной интерпретации V(S) как гарантированного выигрыша коалиции S, в том случае, когда она действует независимо от остальных игроков. Выполнение свойства супер-аддитивности говорит о целесообразности объединения игроков с точки зрения суммированного выигрыша. ] - доля i-ого игрока при распределении максимального суммарного выигрыша v{N}, вектор удовлетворяет условиям индивидуальной рациональности, т. е. и коллективной рациональности, т. е. - называется дележом.