
2.3 Алгоритм вычисления.
Основными функциями программы является функции From4To3, From3To2 и From2To1 «понижение ранга матрицы».
Public class BasicFunctions
{
// Понижение ранка матрицы с 4 до 3
public double From4To3(int a)
{
int I,j;
// Initialize P4
for (I = 0; I < 4; i++)
{
for (j = 0; j < 4; j++)
{
Globals.P4[I, j] = Globals.P5[I + 1, j + 1];
}
}
// Counting necessary row
for(j=0;j<4;j++)
{
Globals.P4[a-1, j] = Globals.P4[a-1, j] * Globals.P5[0, j+1];
}
// Quantifying 4rd rank matrix
return Convert.ToDouble((1 – Globals.P4[0, 1]) * From3To2(1) + (1 – Globals.P4[0, 2]) * Globals.P4[0, 1] * From3To2(2) +
(1 – Globals.P4[0, 3]) * Globals.P4[0, 1] * Globals.P4[0, 2] * From3To2(3));
}
// Понижение ранка матрицы с 3 до 2
public double From3To2(int k)
{
int I, j;
// Initialize P3
for (I = 0; I < 3; i++)
{
for (j = 0; j < 3; j++)
{
Globals.P3[I, j] = Globals.P4[I + 1, j + 1];
}
}
// Counting necessary row
for (j = 0; j < 3; j++)
{
Globals.P3[k – 1, j] = Globals.P3[k – 1, j] * Globals.P4[0, j + 1];
}
// Quantifying 3nd rank matrix
return Convert.ToDouble((1 – Globals.P3[0, 1]) * From2To1(1) + (1 – Globals.P3[0, 2]) * Globals.P3[0, 1] * From2To1(2));
}
// Понижение ранка матрицы с 2 до 1
public double From2To1(int m)
{
int I, j;
// Initialize P2
for (I = 0; I < 2; i++)
{
for (j = 0; j < 2; j++)
{
Globals.P2[I, j] = Globals.P3[I + 1, j + 1];
}
}
// Counting necessary row
for (j = 0; j < 2; j++)
{
Globals.P2[m – 1, j] = Globals.P2[m – 1, j] * Globals.P3[0, j + 1];
}
// Quantifying 2nd rank matrix
return Convert.ToDouble((1 – Globals.P2[0, 1]));
}
2.4 Пример функционирования программы
Основная форма:
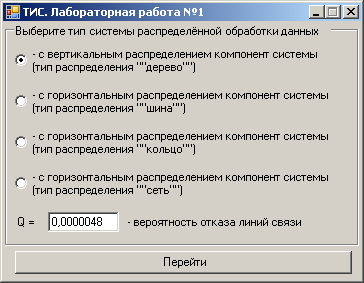
Рис. 9. Форма выбора типа системы.
Форма топологии “дерево”
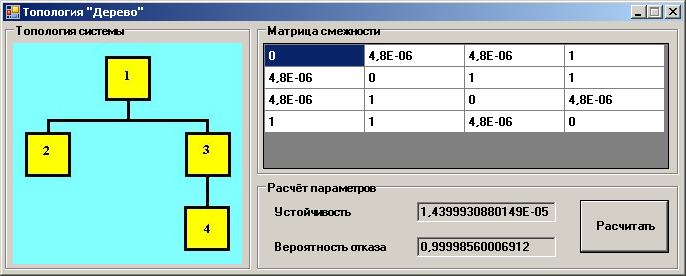
Рис. 10. Тип распределения «Дерево»
Форма топологии “шина”
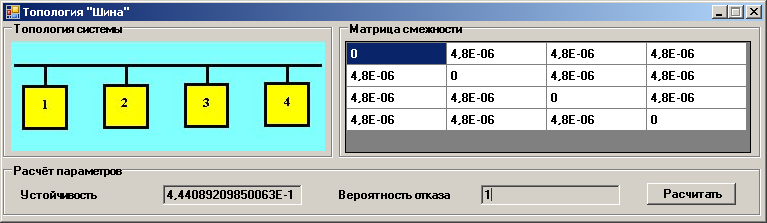
Рис. 11. Тип распределения «Шина»
Форма топологии “кольцо”
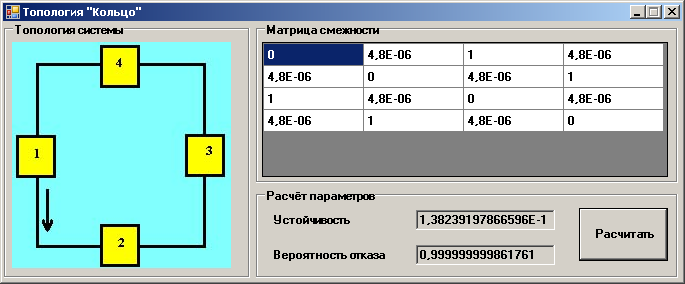
Рис.12. Тип распределения «Кольцо»
Форма топологии “сеть”
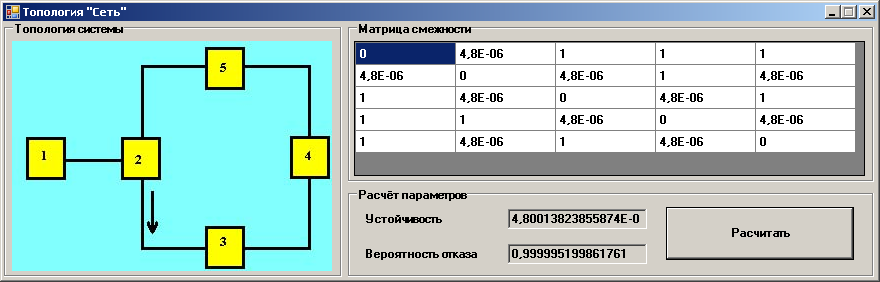
Рис. 13. Тип распределения «Сеть»
4 Вывод
В результате выполнения данной лабораторной работы были рассмотрены основы топологического анализа систем, метод матричного вычисления вероятности связного графа. Написана программа для вычисления вероятностей отказа систем распределенной обработки данных при распределениях типа «дерево», «шина», «кольцо», «сеть». Результаты показали, что наибольшую устойчивость имеют системы топологий «дерево» и «шина», а наименее устойчива система с топологией «кольцо».
