Тема 4. Абсолютные и относительные величины в статистике

1. Понятие статистического показателя.

2. Системы статистических показателей.

3. Абсолютные показатели, единицы их измерения и виды.

4. Виды относительных статистических показателей.

5. Обобщающие показатели структурных различий.

Статистика дает количественную характеристику массовых социально-экономических явлений, оперируя при этом числами. Но числа, применяемые в статистике — это не абстрактные величины, как, например, в математике, они отражают внутреннее содержание изучаемых явлений. Собственно говоря, данные числа — это статистические показатели.

Статистический показатель — это обобщающая количественная характеристика какого-то свойства совокупности или группы.

Статистические показатели образуются на этапе статистической сводки, на котором путем суммирования осуществляется переход от индивидуальных значений признаков у отдельных единиц совокупности к показателям совокупности, называемым обобщающими или сводными. Но процесс получения обобщающих показателей не ограничивается только суммированием. Например, если известна общая численность студентов на курсе и получен суммарный балл успеваемости, можно рассчитать средний балл успеваемости на данном курсе, который также будет сводным показателем. Зная численность юношей и девушек, обучающихся на курсе, можно рассчитать удельный вес этих групп в общей численности студентов, который является относительным статистически показателем.

Поскольку совокупности явлений или процессов имеют целое множество свойств, связанных между собой, то и статистические показатели, отражающие эти свойства, не являются изолированными друг от друга, а в большинстве случаев представляют систему показателей.

Система статистических показателей — это совокупность взаимосвязанных показателей, имеющая одноуровневую или многоуровневую структуру и нацеленная на решение конкретной статистической задачи. Например, система показателей предприятия может быть представлена абсолютными показателями (списочная численность работников, стоимость основных фондов и оборотных средств, фонд заработной платы, прибыль и др.), относительными (фондоотдача, фондовооруженность, производительность труда, процент выполнения плана и др.) и средними показателями (средняя заработная плата одного работника, средняя списочная численность работников, среднее фактическое число часов, отработанных одним работником за период и др.).

Система статистических показателей обязательно должна включать и абсолютные, и относительные показатели. Только в этом случае можно ожидать наиболее полного и объективного отражения процесса или явления.

В зависимости от методов расчета обобщающие показатели могут быть абсолютными, относительными и средними величинами.

Абсолютные показатели отражают физические размеры изучаемых статистикой процессов и явлений, а именно их массу, площадь, объем, протяженность, временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц. К абсолютным показателям, например, относятся площадь территории страны, объем промышленного производства, эксплуатационная длина железнодорожных путей сообщения, число предприятий отрасли и т.п.

Абсолютные статистические показатели всегда являются именованными числами. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или условно-натуральных единицах измерения.

В статистической практике для аналитических целей широко применяются относительные показатели. Относительный показатель представляет собой результат деления одного абсолютного или относительного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений. Поэтому по отношению к абсолютным показателям относительные показатели, или показатели в форме относительных величин, являются производными, вторичными. Без относительных показателей невозможно измерить интенсивность развития изучаемого явления во времени, оценить уровень развития одного явления на фоне других взаимосвязанных с ним явлений, осуществить пространственно-территориальные сравнения, в том числе и на международном уровне.

При расчете относительного показателя абсолютный показатель, находящийся в числителе получаемого отношения, называется текущим или сравниваемым. Показатель же, с которым производится сравнение и который находится в знаменателе, называется основанием, или базой сравнения. Таким образом, рассчитываемый относительный показатель указывает, во сколько раз сравниваемый абсолютный показатель больше базисного, или какую долю он от него составляет, или сколько единиц первого приходится на 1, 100, 1000 и т.д. единиц второго.

Относительный показатель может выражаться в коэффициентах, процентах, промилле, продецимилле или быть именованным числом. Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000 или 10000, то относительный показатель соответственно выражается в процентах (%), промилле (⁰/₀₀) и продецимилле (⁰/₀₀₀).

Все используемые на практике относительные статистические показатели можно подразделить на следующие виды: показатели динамики, плана, реализации плана, структуры, координации, интенсивности и уровня экономического развития, сравнения.

Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) и уровня этого же процесса или явления в прошлом:

Рассчитанная таким образом величина показывает, во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего он составляет. Данный показатель может быть выражен кратным отношением или переведен в проценты.

Различают относительные показатели динамики с постоянной и переменной базами сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем, например, первым годом рассматриваемого периода, получают относительные показатели динамики с постоянной базой (базисные). При расчете относительных показателей динамики с переменной базой (цепных) сравнение осуществляется с предшествующим уровнем, т.е. основание относительной величины последовательно меняется.

Все субъекты финансово-хозяйственной сферы, начиная от небольших предприятий и заканчивая крупными концернами, в той или иной степени осуществляют перспективное планирование своей деятельности, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели используются относительные показатели плана (ОПП) и реализации плана (ОПРП).

Относительный показатель плана (ОПП) — характеризует напряженность плана, т.е. во сколько раз намеченный объем производства должен превысить достигнутый или сколько процентов от него составить

где i — номер периода.

Относительный показатель реализации плана (ОПРП) — отражает фактический объем производства в процентах или в коэффициентах к планируемому уровню

Первый из показателей характеризует напряженность плана, т.е. во сколько раз намечаемый объем производства превысит достигнутый уровень или сколько процентов от этого уровня составит. Второй показатель отражает фактический объем производства в процентах или коэффициентах по сравнению с плановым уровнем.

Относительный показатель структуры (ОПС) представляет собой отношение структурных частей изучаемого объекта и их целого:

Выражается относительный показатель структуры в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.

Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:

Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:

Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства. Так как объемные показатели производства по своей природе являются интервальными, а показатель численности населения — моментным, в расчете используют среднюю за период численность населения (например, среднегодовую).

Относительный показатель сравнения (ОПСр) представляет собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, районы, области, страны и т п.):

Структура — это строение, форма организации совокупности, состоящей из отдельных элементов, единиц или групп совокупности.

Структура характеризуется с помощью показателей удельного веса, доли отдельных элементов в общей численности совокупности.

Для анализа изменения структуры совокупности во времени используют различные обобщающие показатели структурных сдвигов. Наиболее часто рассчитывают линейный коэффициент абсолютных структурных сдвигов:

где — удельные веса (в %) отдельных элементов совокупности в рассматриваемом и предыдущем периодах; — число выделяемых элементов совокупности.

Чтобы избежать взаимопогашения разных по знаку изменения долей, вместо модулей иногда применяют квадраты отклонений и получают квадратический коэффициент абсолютных структурных сдвигов:

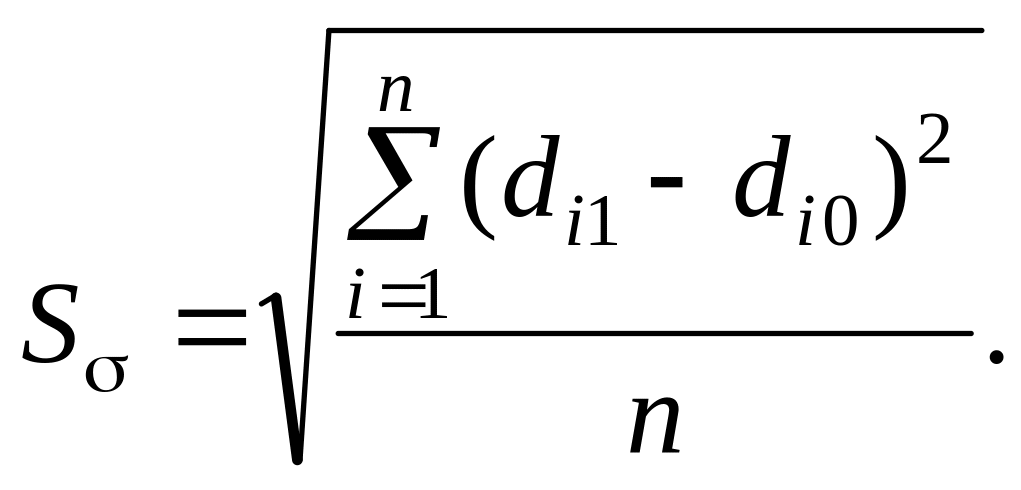
Линейный и квадратический коэффициенты абсолютных структурных сдвигов показывают, на сколько процентных пунктов в среднем отклоняются друг от друга сравниваемые удельные веса. При отсутствии сдвигов в структуре совокупности эти показатели равны 0. Верхней границы изменения коэффициенты не имеют: чем больше изменения структуры, тем выше значения коэффициентов. Использование квадратического коэффициента предпочтительнее, так как он более чутко реагирует на сильные колебания структуры.

К наиболее простым сводным показателям структурных сдвигов относят и индекс различий, который в отличие от предыдущих коэффициентов имеет не только нижнюю, но и верхнюю границу изменения:

где — показатели удельного веса, выраженные в долях.

Очевидно, что максимальная сумма модулей изменения долей может быть равна 2. Это возможно в гипотетической ситуации, когда в одном периоде вся совокупность сосредоточена в одной группе, а в следующем периоде — в другой. Поэтому теоретически индекс различий может иметь верхнюю границу, равную 1, однако в действительности он всегда меньше 1. Если изменений в структуре не происходило, индекс различий будет равен 0. Таким образом, 0 < < 1. Чем ближе значение индекса различий к 1, тем более значительны изменения структуры.