3.2. Надежность системы с нагруженным дублированием

Способ нагруженного дублирования является частным случаем общего нагруженного резервирования с целой кратностью, m = 1, то есть на одну основную цепь приходится одна резервная цепь, находящаяся под нагрузкой. На рис. 6.4 (изображена расчетная схема надежности).

Вероятность безотказной работы системы по формуле (6.10)

, (6.13)

где Р_о(t) - вероятность безотказной работы основной цепи ( ).

Среднюю наработку до отказа системы определим по выражению (6.11):

.

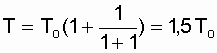Определим зависимость интенсивности отказов системы от времени:

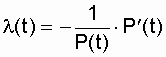. (6.14)

Подставим в выражение (6.14) исходное выражение (6.13) и его производную. После некоторых упрощений получим:

. (6.15)

Для построения графика (t) (рис. 6.5) определим предельные значения этой функции:

;  .

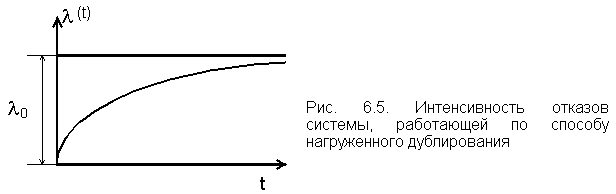
Из рисунка видно что интенсивность отказов системы со временем возрастает. Это говорит о том, что при большом t вероятность отказа одной из цепей высока, и система может перейти в режим работы с одним элементом = ₀. Отметим также начальный этап (когда t  0). Эта система имеет очень высокую надежность ((t) 0).

На рис. 6.6 представлен график функции P(t), построенный по зависимости (6.13). Там же дан график P_о(t) основной цепи (без резерва).

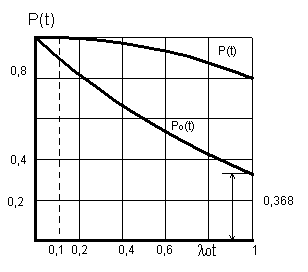
Рис. 6.6. Зависимость вероятностей безотказной работы основной цепи P₀(t) и системы из двух элементов P(t) от  ₀tИз рис. 6.6 видно, на сколько повышается надежность системы (схемы), переведенной в режим нагруженного дублирования. Если учесть, что в системе электроснабжения при профилактических работах, связанных с подготовкой электроустановок к работе зимой или для производства летних работ, многие электроустановки планово отключаются два раза в год, то при Т_о  10 лет,  1/год, t = 0,5 года ( ), значение Р(t = 0,5)  0,999. Этого уровня надежности электроснабжения широкого круга потребителей зачастую оказывается достаточно. В [1] описано каким образом за счет технического обслуживания достигается высокий уровень надежности неремонтируемых систем, работающих по способу нагруженного дублирования значительное время.

Практическая РАБОТА № 2 (4 часа)

Расчет надежности проектируемых систем

Цель работы: Изучение метода дифференциальных уравнений.

Теоретическая часть

Метод основан на допущении о показательных распределениях времени (наработки) между отказами и времени восстановления. Параметр потока отказов ==1/m_t, интенсивность восстановления =1/m_tв, где m_t - среднее время до отказа (между отказами); m_tв - среднее время восстановления.

Метод дифференциальных уравнений может быть использован при расчете надежности как восстанавливаемых, так и невосстанав­ливаемых систем. Для применения метода необходимо иметь матема­тическую модель в виде множества состояний системы, в которых она может находиться при отказах и восстановлениях элементов.

Чтобы определить показатели надежности, составляют и реша­ют систему дифференциальных уравнений для вероятностей состоя­нии (уравнений Колмогорова).

Обычно предполагают, что отказавшие объекты начинают не­медленно восстанавливаться и отсутствует число ограничений на число восстановлений.

Математическую модель обычно изображают в виде графа (схемы) состояний, ниже приведен пример графа состояний.

_n ₁

. _n ₁

. ₃ ₃ ₂ ₂

.

При невосстанавливаемой системе между состояниями имеется лишь по одной стрелке.

Для определения вероятностей p_j(t) нахождения системы в момент времени t в j-м состоянии можно составить по графу состояний систему обыкновенных дифференциальных уравнений.

Для приведенного графа состояний имеем:

;

;

.

.

.

Уравнение для состояния 0 опускается из-за громоздкости. Система дифференциальных уравнений дополняется нормировочным условием .

Все множество возможных состояний системы разбивается на два: подмножество состояний n₁, в которых система находится в работоспособном состоянии и n₂ – подмножество неработоспособных состояний.

Когда выписывают коэффициент готовности или коэффициент простоя (перерывы в работе системы допустимы), рассматривают установившийся режим эксплуатации при . При этом все производные и система дифференциальных уравне­ний переходит в систему алгебраических уравнений.

Рассмотрим в качестве примера вычисление коэффициента готов­ности К_ГС системы, состоящей из n элементов, коэффици­енты готовности которых К_Г1,К_Г2, … К_Гn . При отказе одного из элементов отказывает вся система.

Граф состояний системы изображен выше. На графе обозначены следующие возможные состояния:

0 - все элементы работоспособ­ны;

1- элемент неработоспособен, остальные работоспособны;

2 - второй элемент неработоспособен, остальные работоспособны;

3 - третий элемент неработоспособен, остальные работоспособны и т.д.

Вероятности одновременного появления двух неработоспособных элементов пренебрежимо малы. Символами , ,… обозначены интенсивности отказов; , ,…, - интенсивности восстановления соответствующих элементов. При установившемся режиме эксплуатации

;

;

.

.

.

Решив полученную систему алгебраических уравнений, с учетом нормировочного условия получим

. (1)

Вероятность нахождения в j -м состоянии .

Из соотношения имеем: (2)

Подставив (2) в (1), получаем

.

Пусть, например, К_Г1=0,61; К_Г2=0,72; К_Г3=0,63.

Получаем

.