31. Устойчивость лсау и лсар. Логарифмический критерий устойчивости.

Под устойчивостью САУ (САР) подразумевается свойство системы возвращаться к первоначальному состоянию после прекращения внешнего воздействия, выведшего систему из такого состояния. Если ограничения на x(t) есть, то система устойчива в малом. Если ограничений нет, то в большом.

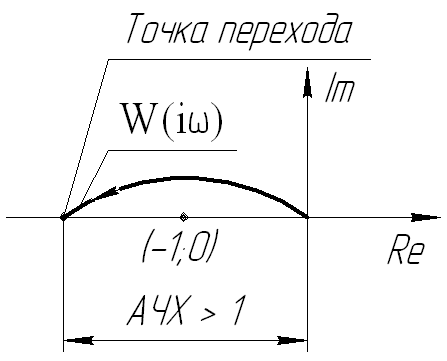
Другая формулировка критерия Найквиста – ЛКУ.

Точки перехода – точки в которых

Если переход при увеличении ω происходит снизу вверх то он считается положительным (П↑), а если сверху вниз то он считается отрицательным (П↓).

Критерий:

Если l число корней характеристического уравнения разомкнутой системы лежащих в правой полуплоскости, то необходимым и достаточным условием устойчивости замкнутой системы АУ является следующее равенство

Следствие:

Для систем устойчивых в разомкнутом состоянии, необходимым и достаточным условием равновесия является следующее равенство:

.

Т.к. l=0, т.е. нет корней в правой полуплоскости.

32.Исследование качества лсау и лсар.

Показатели качества переходного процесса.

1.Подаём на вход системы единичную функцию (функцию Дирака)

и смотрим на изменение переходной функции;

1,2,3-процесс без перерегулирования;

4-процесс с перерегулированием (h(t)>h(∞))

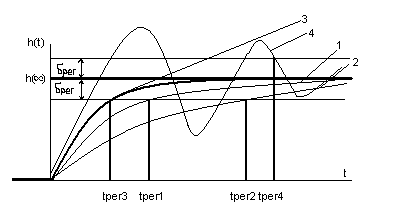
2.Время переходного процесса

δрег≈5% h(∞) не более

3.σ-величина перерегулирования (%)

4.N- колебательность процесса (число перерегулирований)

33. Исследование качества лсау и лсар. Запас устойчивости по фазе и амплитуде.

Начальные условия.

Будем считать, что исходная разомкнутая система устойчива. Годограф не должен охватывать точку (-1;0)

C - точка среза, ω_с - частота, при которой годограф ЧХ РС пересекает единственную окружность, называется частотой среза.

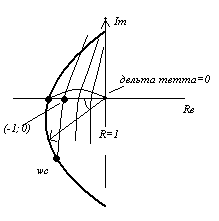
ω_π - частота, которая соответствует фазе = 180°. (Где пересекает горизонтальную – вещественную ось)

Δθ-запас устойчивости по фазе

Запасом устойчивости САУ по фазе называется угол Δθ = 180° - θ₁, где θ₁-значение фазы, при котором АЧХ=|W(iω)|=1, или ЛАЧХ=0.

Запас по фазе показывает насколько нужно изменить фазу системы, не изменяя ее амплитуду, чтобы устойчивая прежде система оказалась на грани устойчивости.

Для устойчивых систем: Δθ > 0. Чем больше Δθ, тем больше запас.

Для неустойчивых систем: Δθ > 0

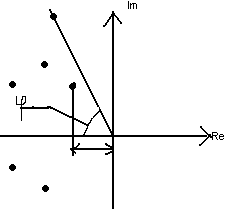
Запасом устойчивости по амплитуде называется величина β, где

β показывает во сколько раз необходимо увеличить (для неустойчивых САУ - уменьшить) амплитуду при неизменных значениях других параметров, чтобы устойчивая система оказалась на грани неустойчивости.

34. Интегральные характеристики качества лсау и лсар.

Чем больше λ₀, тем больше запас устойчивости.

Чем меньше μ, тем меньше колебательность процесса.

Эти же критерии можно использовать для переходного процесса:

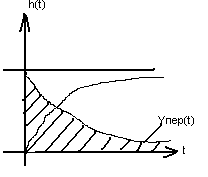
Линейная интегральная оценка качества переходного процесса:

Чем меньше площадь, тем больше быстродействие.

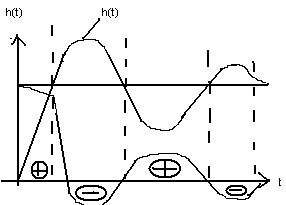
Однако если есть перерегулирование, то эта оценка может сильно врать.

Из этого положения выходят следующим образом:
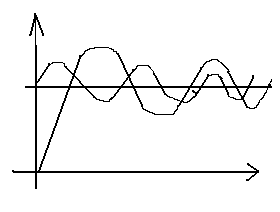