28. Устойчивость лсау и лсар. Алгебраические критерии устойчивости лсау и лсар. Критерий Рауса.

Устойчивость ЛСАУ (ЛСАР) - свойство системы возвращаются к первоначальному состоянию после прекращения внешнего воздействия выведшего систему из такого состояния.

Критерий устойчивости - условие, по которому можно судить об отрицательности вещественных частей корней соответствующего характеристического уравнения не вычисляя их.

Критерий Рауса: Для того, чтобы ЛСАУ была устойчивой необходимо и достаточно, чтобы в преобразованном к треугольному виду определителе Гурвица все члены на главной диагонали были положительны.

Полиномом Гурвица D(p) в степени n≥1 называется такой полином, у которого все корни p_j, j=1,…,n расположены в левой полуплоскости.

Если полином

стандартный, то выполняется условие a₀ ≠ 0 и a_n > 0.

Пример:

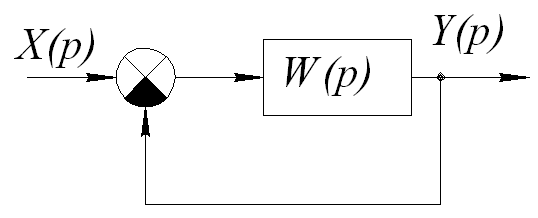
30. Устойчивость лсау и лсар. Частотные критерии. Критерий Найквиста.

Он позволяет по характеристикам разомкнутой системы судит о характеристиках замкнутой системы.

Введём вспомогательную функцию

Где l - число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Теорема Найквиста.

Необходимым и достаточным условием устойчивости замкнутой системы является то, что изменение фазы вспомогательной функции В(iω) при 0≤ω<∞ будет равняться

Где l- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Необходимым и достаточным условием устойчивости замкнутой системы является тот факт, что годограф вспомогательной функции В(iω) должен огибать начало координат при 0≤ω<∞ в положительном направлении (против часовой стрелки) на угол lπ , где l- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Критерий Найквиста.

Для устойчивости ЛСАУ необходимо и достаточно, чтобы годограф ЧХ разомкнутой системы W(iω) при изменении 0≤ω<∞ охватывал точку (-1;0) на угол lπ в положительном направлении, где l- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Следствие.

Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф ЧХ разомкнутой системы W(iω) при изменении 0≤ω<∞ не охватывал точку (-1;0) на угол lπ в положительном направлении, где l- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

29. Устойчивость лсау и лсар. Частотные критерии устойчивости лсау и лсар. Критерий Михайлова.

Левая часть характеристического уравнения:

где p_j – корни D(p):

Получим функцию Михайлова, подставив в полином D(p) iω вместо аргумента p:

Напоминание из теории комплексных чисел:

Тогда:

Введём вспомогательную функцию:

Тогда:

Амплитуда:

Фаза:

При изменении

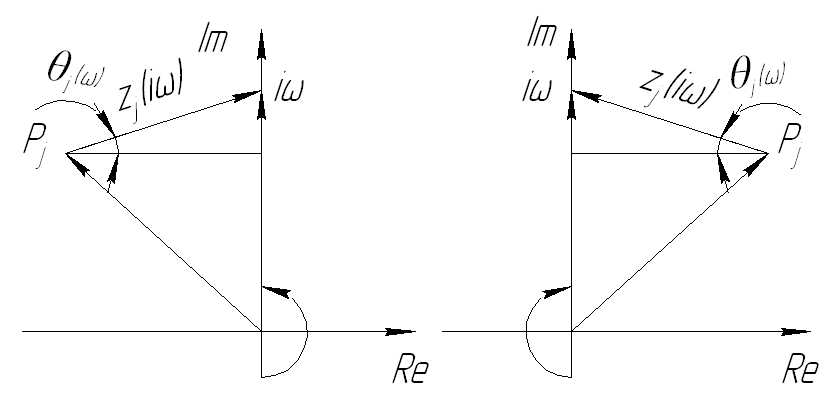
Будем считать угол положительным, если он направлен против часовой стрелки, и отрицательным, если по часовой.

Пусть характеристическое уравнение имеет n корней p_j. Из них l корней лежит в правой полуплоскости, а (n-l) – в левой полуплоскости.

Теорема Михайлова.

Для устойчивости ЛСАУ, имеющей характеристическое уравнение необходимо и достаточно, чтобы изменение фазы функции Михайлова равнялось , при изменении .

Построим годограф функции Михайлова D(iω) при .

- чётная функция;

- нечётная функция;

Следовательно, годограф функции Михайлова является симметричным относительно вещественной горизонтальной оси. Поэтому можно принять .

Под годографом Михайлова будем понимать геометрическое место точек, которые оставляет на комплексной плоскости конец вектора функции Михайлова при изменении .

Критерий Михайлова.

Для устойчивости ЛСАУ необходимо и достаточно, чтобы годограф Михайлова, начинающийся при ω=0 на положительной части вещественной (Re) оси при увеличении ω от 0 до обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n – порядок соответствующего характеристического уравнения .