8. Передаточная функция лсау и лсар. Свойства передаточной функции. Интеграл Дюамеля.

x(t), y(t)-оригиналы.

Функция W(p)=Y(p)/X(p) – представляющая собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала в пространстве изображения при нулевых начальных данных - называется передаточной функцией ЛСАУ.

Нулевые начальные данные:

Предположим, что

Тогда:

Передаточная функция:

Свойства передаточной функции ЛСАУ:

2)W(pk)=0 «нули ПФ» ;W(pe)= ∞ «полюса ПФ» -комплексно-сопряженные числа

3)корни K(p)- «нули», корни D(p)- «полюса».

Интеграл Дюамеля:

оригинал ПФ

Интеграл Дюамеля определяет выходной сигнал системы при нулевых начальных данных в виде свертки оригинала ПФ и входного сигнала.

9.Переходная функция ЛСАУ и ЛСАР и ее свойства.

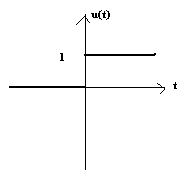
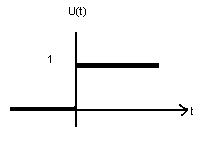
Сигнал h(t), полученный на выходе системы при подаче на вход единичной функции u(t) называется переходной функцией системы.

Дифференцируем это выражение и получаем, что оригинал передаточной функции есть производная от переходной функции.

10. Весовая функция ЛСАУ и её свойства.

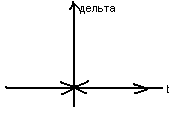
Функция Дирака или δ-функция (единичный импульс)

Свойства функции Дирака:

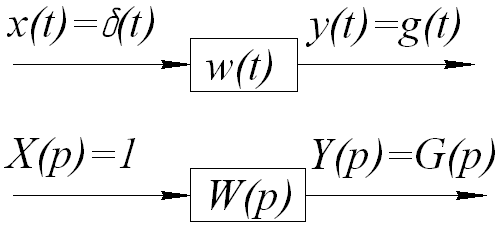
Сигнал, полученный на выходе СУ при подаче на его

вход функции Дирака, называется весовой функцией.

12. Типовые звенья ЛСАУ и ЛСАР.

Пропорциональное звено и его характеристики.

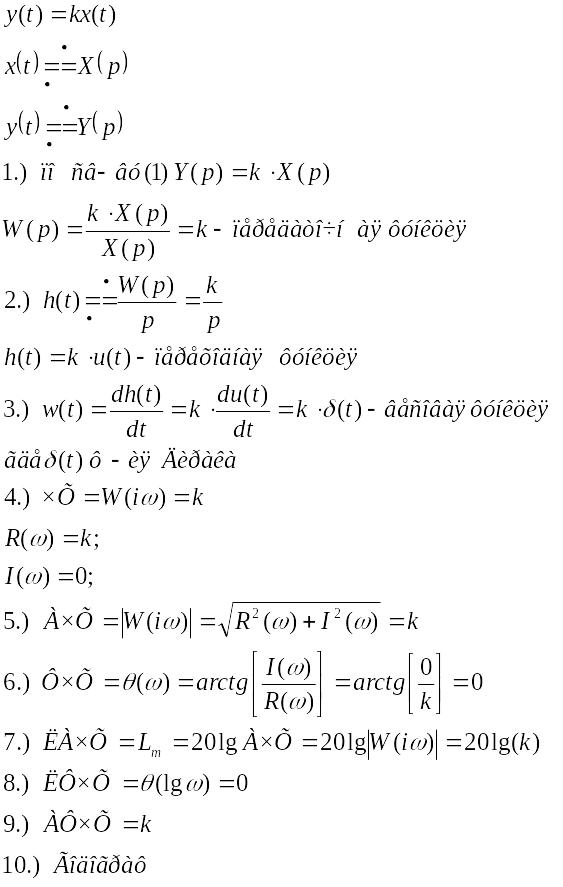
ω	Re(ω)	Im(ω)
0	k	0
-	0	-
-	-	0
+∞	k	0

11. Частотные и логарифмические характеристики ЛСАУ и ЛСАР.

Частотной характеристикой ЛСАУ (эквивалентной комплексной частотной функцией) называется функция W(iω), полученная из передаточной функции W(p) при подстановке iω вместо аргумента p.

Частотная характеристика – ЧХ – это отношение изображения выходного сигнала к изображению входного сигнала в пространстве изображения при нулевых начальных условиях, если в качестве аргументов в них фигурирует гармоническая функция.

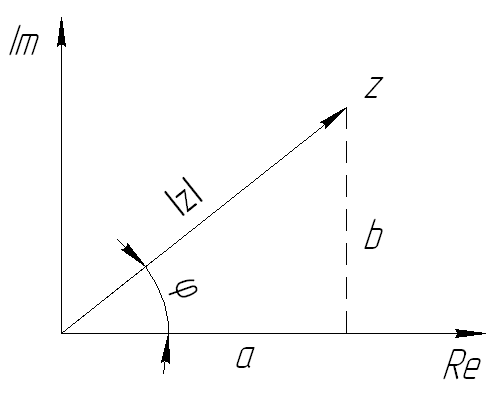
- амплитуда

- фаза

Амплитудно-частотная характеристика (АЧХ):

Амплитудно-частотной характеристикой называется отношение амплитуды на выходе к амплитуде на входе.

Фазо-частотная характеристика (ФЧХ):

Фазо-частотной характеристикой называется отношение фазы на выходе к фазе на входе.

Вводят понятия логарифмической АЧХ и ФЧХ:

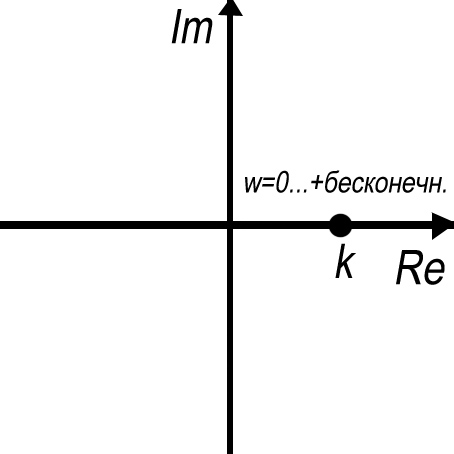
Рассматривая вектор ЧХ W(iω) и варьируя частоту ω в пределах [0;+∞) получаем на комплексной плоскости кривую, описываемую концом этого вектора. Эта кривая называется годографом вектора комплексной частотной функции или амплитудно-фазо-частотной характеристикой (АФЧХ) или годографом ЧХ.

ω – это частота входного сигнала. Это вещественное неотрицательное число.

Характеристики систем:

1. Передаточная функция.

2. Переходная функция.

h(t)

3. Весовая функция.

w(t)

4. Частотная характеристика.

5. Амплитудно-частотная характеристика.

6. Фазо-частотная характеристика.

7. Логарифмическая АЧХ.

8. Логарифмическая ФЧХ.

9. АФЧХ (годограф ЧХ).

13. Типовые звенья ЛСАУ и ЛСАР.

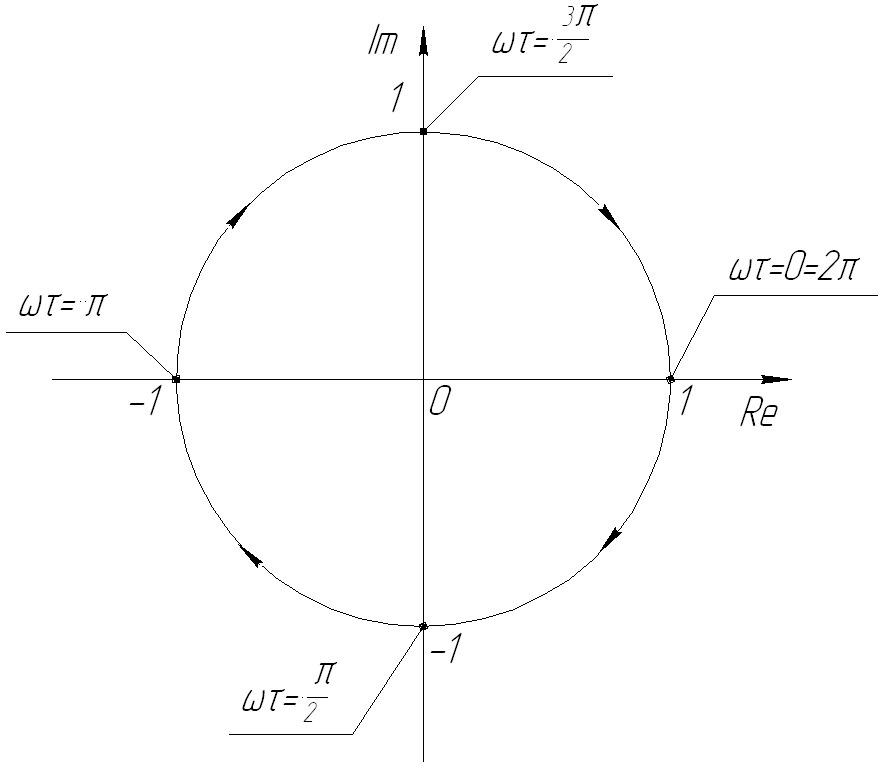
Запаздывающее звено и его характеристики.

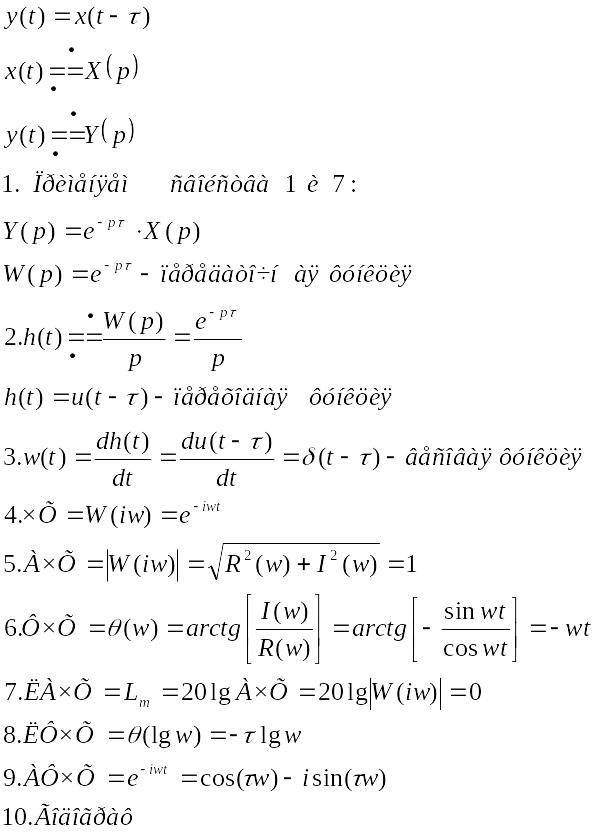
ω	ω τ	Re(ω)	Im(ω)
0	0	1	0
…	π/2	0	-1
…	π	-1	0
…	3 π/2	0	1
∞	2 π	1	0

14. Типовые звенья ЛСАУ и ЛСАР.

Дифференцирующее звено и его характеристики.

ЭВМ, конденсатор, катушка индуктивности.

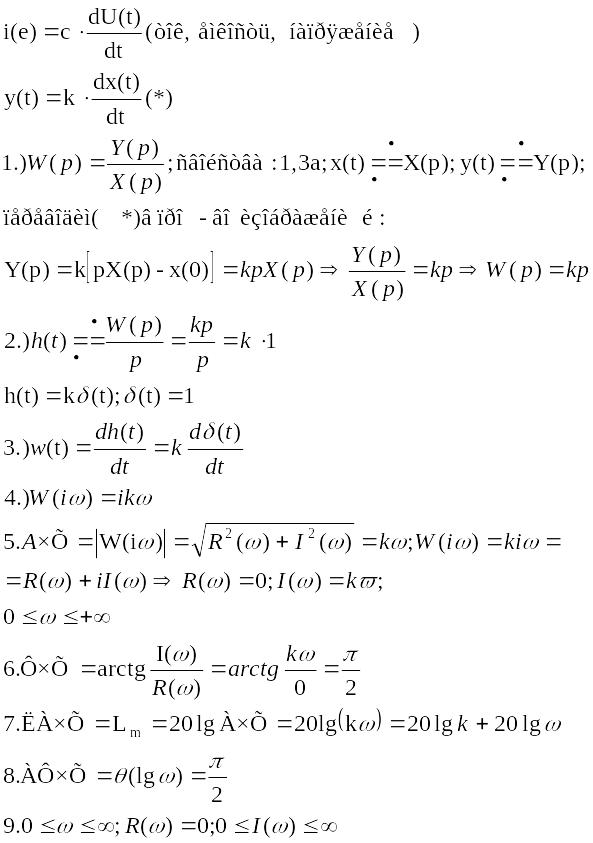
15.Инерционно-дифференцирующее звено.

ω	Re(ω)	Im(ω)
0	0	0
-	0	-
-	-	0
1/T	k/(2T)	k/(2T)
∞	k/T	0

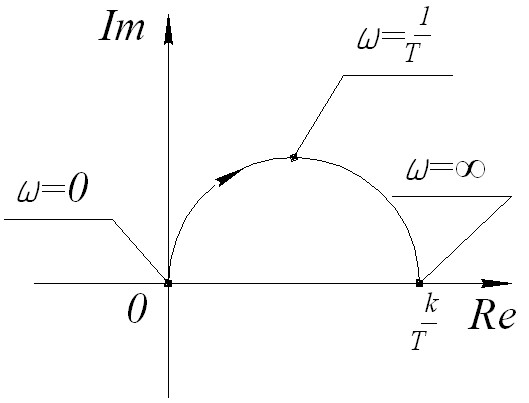
16. Типовые звенья ЛСАУ и ЛСАР. Инерционное звено и его характеристики.

Инерционное звено.

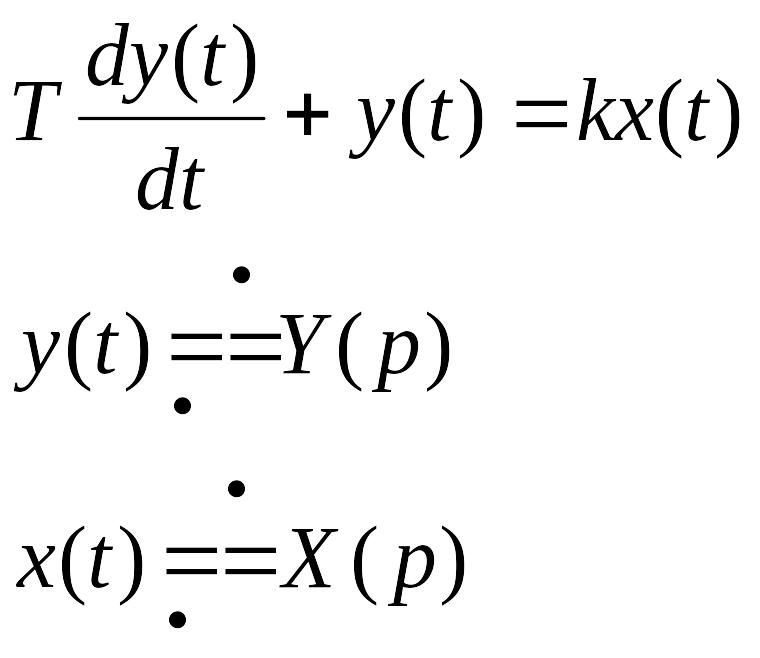
Разложение на простейшие дроби по корням

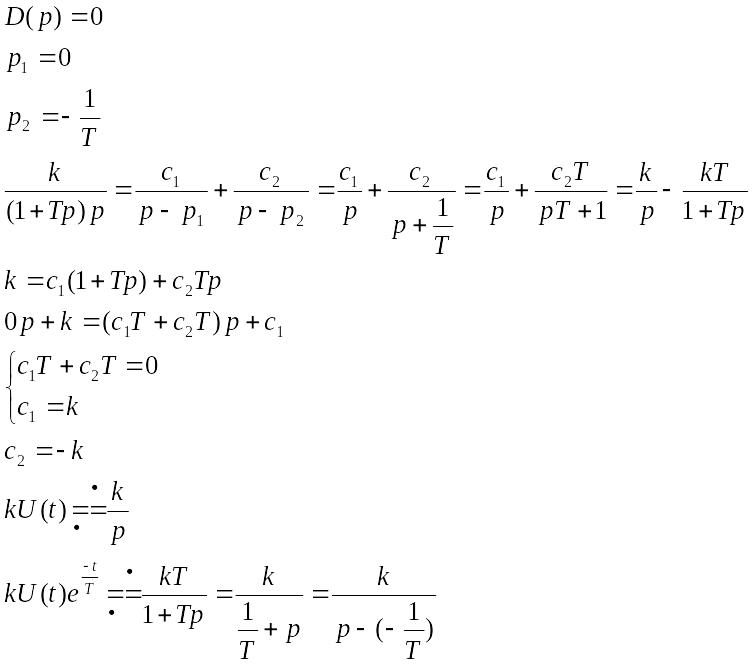
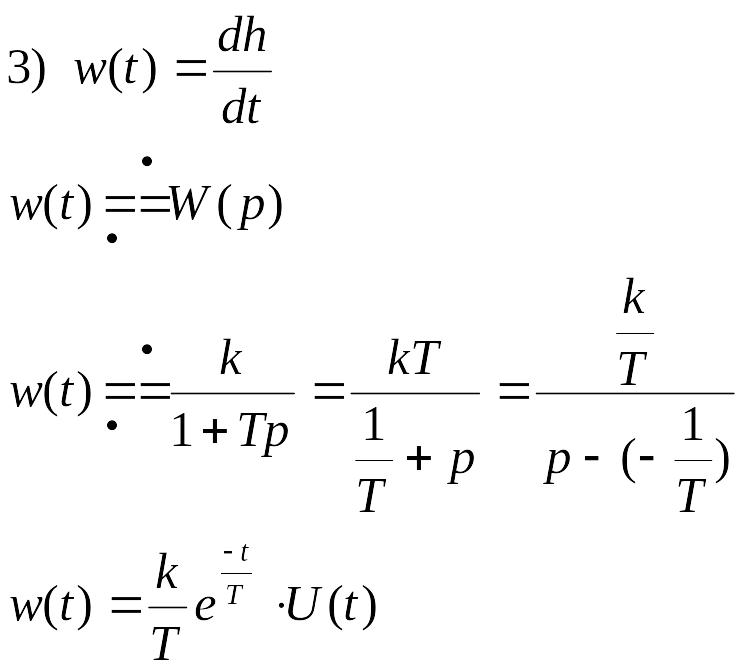
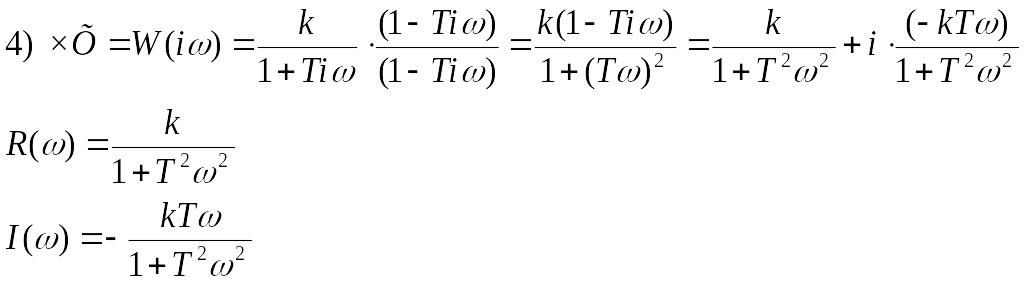
9) Годограф

ω	Re(ω)	Im(ω)
0	k	0
-	0	-
-	-	0
1/T	k/2	-k/2
∞	0	0

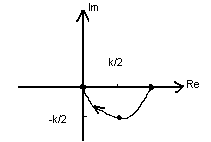
16 вопрос. Продолжение.

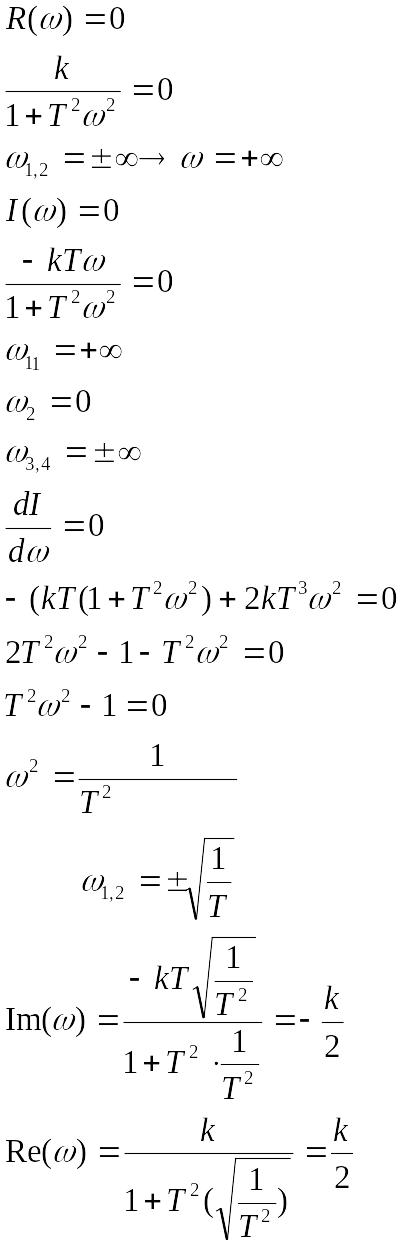
Все типовые звенья делятся на три группы по виду зависимости y(t):

I. 1. Пропорциональное (безинерционное) звено.

k – положительное вещественное число.

2. Запаздывающее звено.

τ - положительное вещественное число.

3. Дифференцирующее звено.

II.1. Инерционно-дифференцирующее звено

(Реальное дифференцирующее звено)

2. Инерционное (апериодическое, реальное, релаксационное) звено.

3. Интегрирующее (астатическое, нейтральное) звено.

4) Интегро-дифференцирующее звено (упругое, инерционно-фарсирующее звено).

k , T– положительные вещественные числа.

III. Колебательное или периодическое.

χ – (каппа) постоянная величина > 0