5. Математическое описание сау и сар. Моделирование сау и сар. Разбиение сау и сар на звенья. Статические и динамические характеристики звеньев сау и сар.

Моделирование САУ(САР)

Существует два подхода

1. Физический эксперимент

2. Математическое описание

Разбиение САУ (САР) на звенья. Структурная схема.

Элементы направленного действия – элементы, у которых выходной сигнал не влияет на входной.

Звено – часть системы управления, которая осуществляет некоторое преобразование входного сигнала в выходной, являясь элементом направленного действия.

1. Алгоритм преобразования входного сигнала в выходной.

2. Элемент направленного действия.

3. Не обязательно обособленность звена.

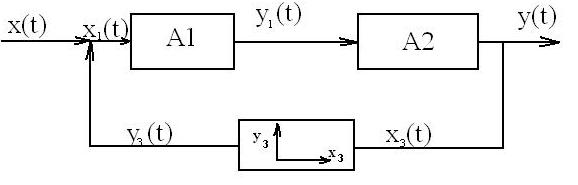
Структурной схемой САУ (САР) называется схема, показывающая из каких звеньев она состоит и как эти звенья соединены между собой.

Если разбить систему управления на звенья, то математическое описание каждого звена может быть выполнено без учета его связи с другими звеньями.

Математическое описание всей САУ (САР) – совокупность составленных независимо друг от друга уравнений звеньев системы.

Статические характеристики звеньев.

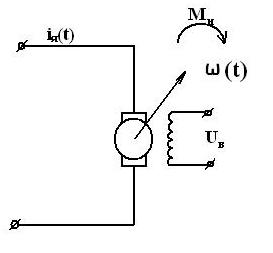
Статистические характеристики звена – зависимость между выходной величиной y этого звена от входной x в установленном режиме при разных воздействиях на это звено.

Фиксируем входной сигнал х и фиксируем внешнее воздействие f и измеряем y.

- Статические характеристики звена.

Фиксируем нагрузку, ток и угловую скорость и снимаем точку, затем меняем значения, все то же самое, и получаем вторую точку и т. д.

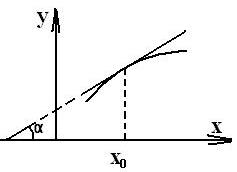
Коэффициент усиления звена:

Динамические характеристики звеньев.

Уравнение движения звена – уравнение(или система уравнений), определяющее изменение во времени выходной величины y по заданному измеренному во времени входной величине вектора x.

Существует два случая:

1. Меняется x, и меняется y.

2. Когда звено переходит из одного установившегося состояния в другое (x - фиксировано)

Линейная система.

Системы со сосредоточенными параметрами.

1) Линейные алгебраические уравнения – ЛСАУ.

2) Линейные дифференциальные уравнения – СДУ (линейных).

3) Интегральные системы – (содержат интегралы).

n>m

n>q

устоявшееся уравнение статики:

6. Математическое описание сау и сар. Моделирование сау и сар. Примеры составления дифференциальных уравнений звеньев сау и сар. Составление дифференциальных уравнений сау и сар в целом.

Моделирование САУ(САР)

Существует два подхода

1. Физический эксперимент

2. Математическое описание

Примеры составления дифференциальных уравнений звеньев САУ и САР.

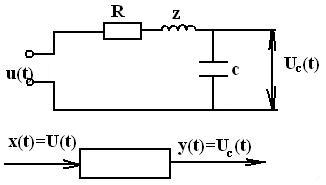
Составление дифференциальных уравнений САУ и САР в целом.

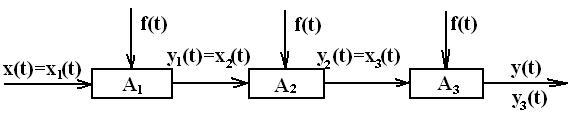
7. Линейные системы автоматического управления и регулирования (лсау и лсар). Общие сведения. Передаточная функция лсау и лсар.

САУ или САР линейные, если уравнения динамики и следовательно статики линейны. Характерной чертой линейной системой автоматического управления и регулирования является применимость к ним принципа суперпозиции.

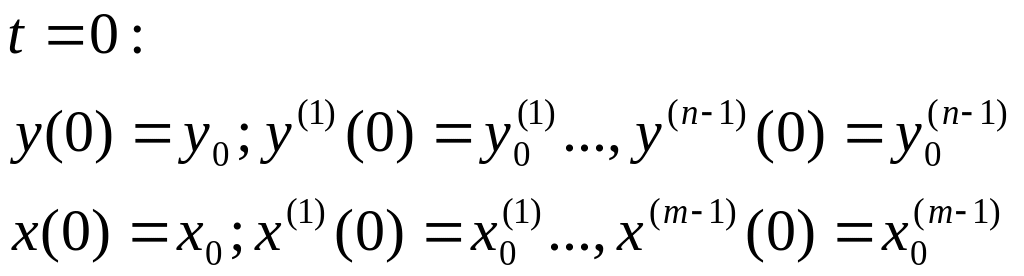
где (t) – общее решение однородного уравнения

y(t) – частное решение неоднородного уравнения

Передаточная функция ЛСАУ.

x(t), y(t)-оригиналы.

Функция W(p)=Y(p)/X(p) – представляющая собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала в пространстве изображения при нулевых начальных данных - называется передаточной функцией ЛСАУ.

Нулевые начальные данные:

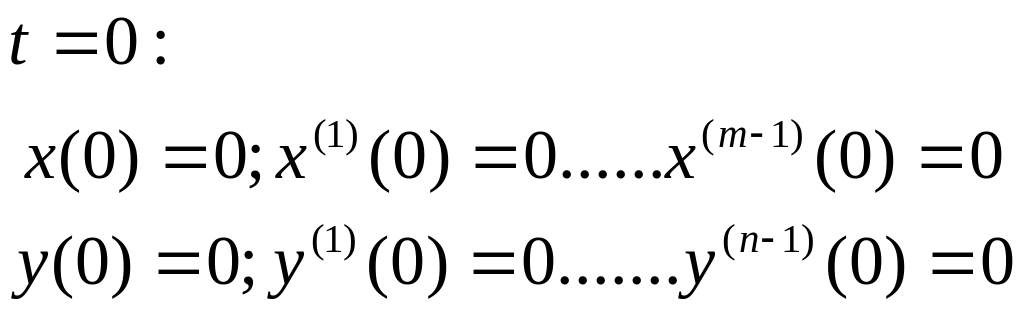
Предположим, что

Тогда:

Передаточная функция: