Момент импульса материальной точки. Момент импульса тела. Закон сохранения момента импульса.

Положим, как и ранее, что твердое тело вращается вокруг некоторой оси неподвижной в пространстве относительно тела (рис. 16). Расчленим тело на малые элементы массами m_i , положение которых в пространстве определяется радиусами-векторами .

Двигаясь по окружности, в некоторый момент времени точка обладает импульсом , а затем под действием силы , которая составляет некоторый угол с касательной. Тогда по 2-му закону Ньютона

_, (89)

Пусть сила остается постоянной. Тогда можно заменить ускорение:

, (90)

Подставим в (28) и получим

, (91)

Умножаем обе части уравнения на радиус-вектор и т.к. масса и радиус-вектор для данной точки не меняются, то их можно внести под знак изменения:

, (92)

Величину называют моментом импульса материальной точки, вращающейся по окружности. В общем случае движения материальной точки по любой траектории под ее моментом импульса подразумевается величина равная произведению ее импульса на длину перпендикуляра, опущенного из точки, лежащей на оси в плоскости вращения на направление вектора скорости (рис. 16).

О

Рис. 16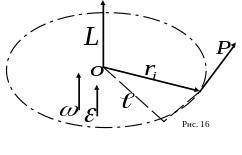

тметим, что момент импульса материальной точки есть векторная величина, имеющая направление вектора угловой скорости перпендикулярного плоскости содержащей вектор импульса точки и радиус-вектор

В левой части уравнения (31) стоит произведение момента силы на время ее действия . Это произведение называют импульсом момента силы, действующим на материальную точку.

Обобщим теперь рассмотренное на случай всего твердого тела. Заменим в уравнении (31) линейную скорость, выразив ее через угловую

, (93)

и умножим обе части уравнения на r_i

, (94)

Просуммируем все материальные точки:

, (95)

В результате получаем

, (96)

где вектор момента сил, действующих на твердое тело,

момент инерции твердого тела.

В виду того что размеры тела не меняются, то его момент инерции остается постоянным, посему его можно внести под знак изменения и окончательно имеем

, (97)

где импульс момента сил, действующих на тело;

момент импульса тела относительно оси вращения.

Т.о. из последней формулы видно, что

Изменение момента импульса твердого тела относительно оси вращения равен импульсу момента приложенных сил относительно той же оси.

Из того же соотношения вытекает, что если момент внешних сил равен нулю (система консервативная), о момент импульса остается постоянным:

, , , (98)

что и составляет суть закона сохранения момента импульса.

В качестве примера проявления или применения закона сохранения импульса можно привести примеры вращений в фигурном катании, акробатике, балете. В технике этот закон необходимо учитывать в кинематической схеме вертолетов: в одних схемах используются два соосных винта, вращающихся в противоположных направлениях или при одном основном пропеллере ставится винт на балке вертолета, создающий момент, компенсирующий момент импульса основного винта. Такой закон проявляется и в космологии. Так сила тяготения, действующая со стороны Солнца не может изменить скорость обращения Земли вокруг сои, ибо в этом случае имеют место только внутренние силы, а по третьему закону динамики сумма этих сил равна нулю. Поэтому сумма моментов импульсов связанная с вращение Луны вокруг Земли и земли вокруг оси подчиняется закону сохранения момента импульса. Т.к. Земля замедляет свою скорость вращения из-за трения приливов и отливов в морях и океанах, которые возникают из-за действия поля Луны, то Луна удаляется от Земли( примерно 1,5 км за столетие). Т.е. возможен вариант, когда периоды обращения Луны вокруг Земли и земли вокруг оси станут равны.