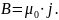§3.4. Энергия электростатического поля.
В параграфе § 2.5. было показано, что энергия электромагнитного поля может быть вычислена по формуле:
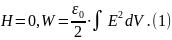
Преобразуем формулу (1) к виду более удобному в некоторых случаях.
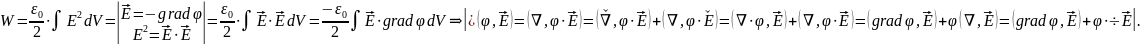
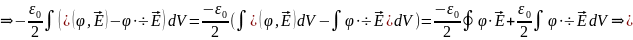
Будем рассматривать замкнутую систему.
–
энергия электростатического поля.
Рассмотрим частный случай системы точечных зарядов.
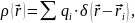
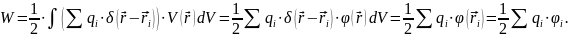
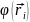– потенциал в точке, в которой находятся
все заряды.
Согласно этой формуле собственная энергия точечного заряда есть:
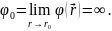
Таким образом, в классической электродинамике собственная энергия точечного заряда оказывается бесконечным.
Этот парадокс является следствием представлений об элементарных зарядах, как точечных объектов, не имеющих размеров. Этот факт указывает об ограниченности классической электродинамики (этим занимается квантовая электродинамика).
Рассмотрим важный частный случай системы заряженных проводников.
Проводник – это вещество, которое проводит при малейшем изменении электрического поля ток.
Напряженность внутри проводника равна нулю.
Получим формулу для расчета энергии такой системы:
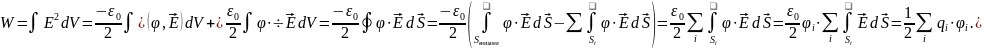
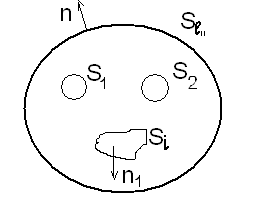
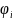– потенциал проводника.
Заряд и потенциал проводника является зависимым величинами, и определяют друг друга.
.
– коэффициенты электростатической
индукции или коэффициенты емкости.
зависят от формы, размеров, материалов
проводников.
.
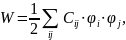
§3.5.Уравнение стационарного магнитного поля. Граничные условия.
Стационарне магнитное поле в вакууме полностью описывается следующими уравнениями:
С математической точки зрения эта система четырех дифференциальных уравнений частных производных первого порядка.
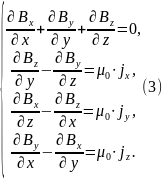
Для решения
основной задачи магнитостатики (то есть
для нахождения
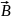по заданному вектору плотности тока
)
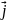необходимо решить систему (3) вместе с
граничными условиями. Однако, на практике
в большинстве случаев удобней пользоваться
методом потенциалов.
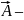векторный потенциал.
С математической точки зрения система (5) оказывается удобней системы (3).
Граничные условия, определяющие скачки компонентов магнитного поля, при переходе через границу раздела двух сред получаются из интегральной формы уравнения (1) и (2) (см. § 3.1.) и имеют вид:
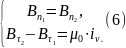
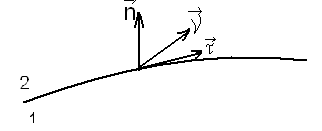
– поверхностная плотность тока в
направлении вектора
на границы раздела.
§3.6. Методы решения задач магнитного поля.
В общем случае решение основной задачи магнитостатики требует решение граничной задачи системы (5). Однако, в некоторых простых случаях удается обойтись более простыми методами. Данные методы аналогична методам решения электростатических задач, рассматриваемых в § 3.4. Рассмотрим их применение на конкретных условиях.
1.) Метод непосредственного интегрирования.
Пример №1.
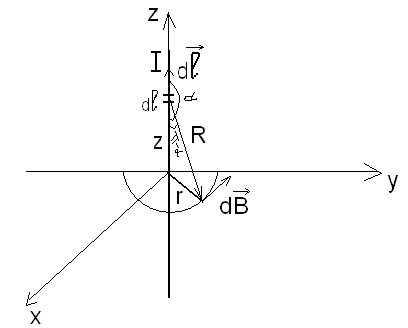
Н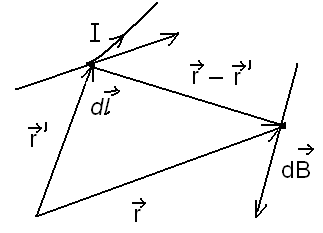
айти
индукцию магнитного поля бесконечного
прямого проводника, по которому течет
сила тока I.
Закон Био-Свара-Лапласа:
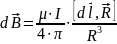
2.) Использование закона полного тока.
Пример №2.
Данный
метод аналогичен методу, основанному
на использовании теоремы Гаусса в
электростатике. В данном методе
используется интегральная форма
уравнения
,
которая носит название полного тока:
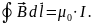
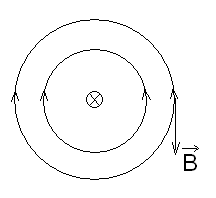
Решим данным методом предыдущую задачу. В качестве вспомогательного контура выбираем окружность с центром.
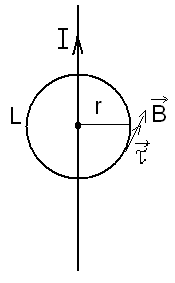
Решение задачи к зачету по электродинамике.
9. В
сферических координатах объемная
плотность заряда внутри шара радиуса
R симметрична относительно
центра шара и имеет вид
.
Используя теорему Гаусса найти
напряженность электрического поля во
всем пространстве.
Решение.
Найдем частный случай для теоремы Гаусса:
1. R<r.
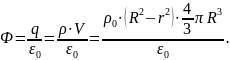
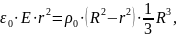
2. r=R
Допустим, что в сфере лежит q:
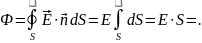
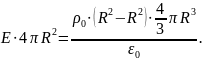
3. R>r.
q=0, так как в выбранной нами воображаемой поверхности нет заряда (q находиться на поверхности шара), значит E=0.
График E(r):
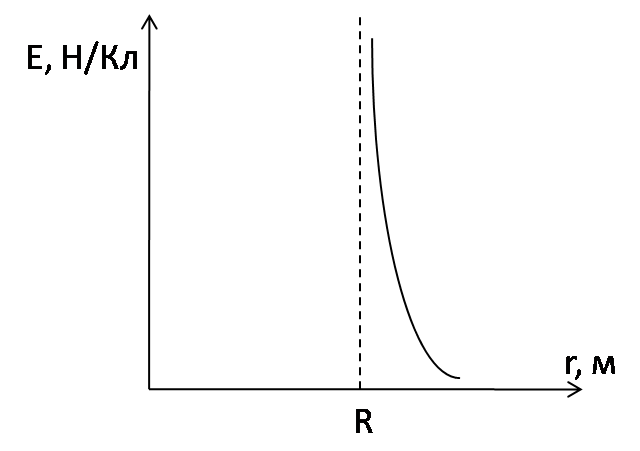
12. В бесконечном проводнике, имеющем форму цилиндра радиуса R, течет постоянный ток с плотностью j. Найти индукцию магнитного поля внутри и снаружи проводника.
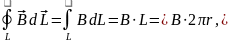
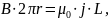
При r>R,
При r<R,
