Глава № 3.
Стационарные поля.
§ 3.1. Уравнение стационарного поля электрического поля.
Граничные условия (уравнения электростатики).
В случае стационарных полей уравнения Максвелла распадаются на две независимых систем уравнений, которые описывают электрические и магнитные поля. В частности уравнение стационарного электрического поля (уравнения электростатики) имеет вид:
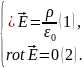
Уравнение
(1) и (2) полностью описывают свойства
электрического поля в вакууме. Однако,
они являются неудобными в математическом
отношении, поэтому при решении основной
задачи электростатики, как правило,
пользуются методом потенциалов. Основной
(прямой) задачей электростатики называется
задачи в определении напряженности
электрического поля по заданной плотности
распространения заряда в пространстве:
В параграфе §2.6 нами были получены уравнения, позволяющие определить потенциалы электрического поля. В стационарном случае:
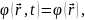
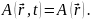
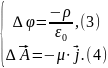
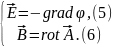
Из уравнений
3–6 видно, что стационарное электрическое
поле определяется только скалярным
потенциалом
и для его нахождения достаточно только
уравнения (3):
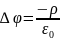– уравнение Пуассона.
С математической точки зрения уравнение Пуассона представляет собой дифференциальное уравнение второго порядка. Как известно (смотри §1.3) для получения однозначного решения таких уравнений, необходимо задать систему начальных и граничных условий (краевая задача).
В стационарном случае начальные условия отсутствуют, задаются только граничные.
Необходимо
в граничных условиях обусловлена тем,
что такие величины, как плотность заряда
,
а также величины описывающие свойства
среды (
– диэлектрическая проницаемость)
меняются скачком при переходе, через
границы раздела двух сред. В этом случае
данные граничные условия определяют
условия сшивки решений, полученных для
каждой из однородных областей.
Получим граничные условия электростатики исходя из интегральной формулы уравнения (1) и (2).
(7)
.
(8)
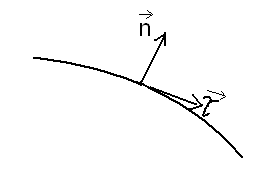
Рассмотрим
циркуляцию напряженности
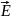по малому прямоугольному контуру l,
который охватывает выбранную точку
раздела поверхности.
.
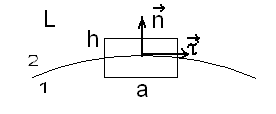
– Сумма интеграла по вертикальным
сторонам.
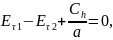При
,
зн.
В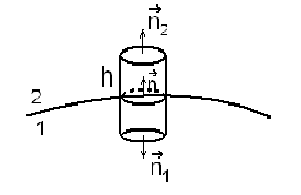
ычислим
поток вектора
,
через поверхность малого цилиндра,
охватывающего заданную точку поверхности
раздела.
При этом будем считать, что в бесконечно тонком поверхностном слое, лежащим на границе раздела, сосредоточены дополнительные заряды, распределенные с поверхностной плотностью ξ.
.
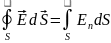Здесь
– проекция вектора напряженности.
Разобьем цилиндр на три части:
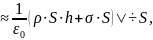
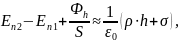
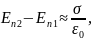
Граничные
условия (9) могут быть записаны в виде
условий накладываемых на потенциал
.
Для этого воспользуемся соотношением:
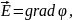
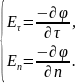
(10) – граничные условия для потенциала.
Уравнение Пуассона вместе с граничными условиями (10) представляют математическую формулировку основной задачи электростатике.
§ 3.2. Электростатика полупроводников и диэлектриков.
План:
1. Электрическое поле в проводнике.
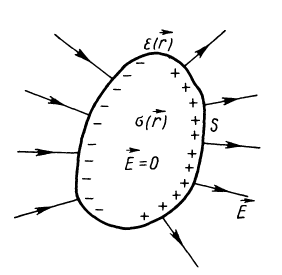
Все тела делятся по электрическим свойствам на диэлектрики и проводники. Изменение электрического поля в проводниках создает ток (движение зарядов). Проводник может иметь заряд q. Напряженность внутри заряженного проводника равна нулю:
.
Заряды в проводниках располагаются только на их поверхностях, поскольку объемная плотность заряда исчезает:
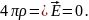
2. Основная задача электростатики для проводников.
Возможны две постановки задачи:
1.) Заданны
потенциалы проводников
,
найти их заряды
и потенциал
2.) Заданны
заряды проводников
,
найти их потенциалы
и потенциал
.
3. Диэлектрическое поле в диэлектриках. Поляризация. Вектор индукции. Диэлектрическая проницаемость.
Основное свойство диэлектриков заключается в невозможности протекания в них постоянного тока. Поэтому, в отличие от проводников, напряженность постоянного электрического поля в диэлектриках отнюдь не должна быть равна нулю, и мы должны получить уравнения, которыми это поле описывается.
,
,
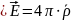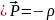Величина
Р называется вектором диэлектрической
поляризации (или просто поляризацией
тела); диэлектрик, в котором Р отлично
от нуля, называют поляризованным. Наряду
с объемной плотностью, вектор Р
определяет также и поверхностную
плотность
зарядов, распределенных по поверхности
поляризованного диэлектрика:
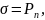где
– составляющая вектора Р по внешней
нормали к поверхности.
Для выяснения физического смысла самой величины Р рассмотрим полный дипольный момент всех внутренних зарядов в диэлектрике; в отличие от полного заряда, эта величина должна быть равна нулю. По определению дипольного момента это есть интеграл:
Таким образом, вектор поляризации представляет собой дипольный момент (или, как говорят, электрический момент) единицы объема диэлектрика.
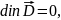
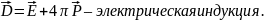
Линейная зависимость D от E приобретает довольно простой вид в важнейшем случае изотропных диэлектрика:
.
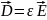– диэлектрическая проницаемость.
