3. Кинематическое исследование механизма двс

3.1 Определение избыточного давления р газов на поршень.

Избыточное давление P_i=h_i∙μ_p∙A, где

h_i – ординаты индикаторной диаграммы, измеренные от линии атмосферного давления по кривой измерения давления в цилиндре.

μ_p – масштаб индикаторной диаграммы.

А – площадь поперечного сечения цилиндра. Находим величину ординат индикаторной диаграммы h_i , соответствующие i-тому положению кривошипа ОА.

Величина избыточного давления.

Положение механизма	Левый цилиндр	Правый цилиндр
4	Р=0 Н	Р= 20001 Н
8	Р=42003 Н	Р=0 Н

м²

3.2 Определение сил инерции звеньев.

Результирующая сила инерции звеньев

Положение №4

Р_и1=0

Р_и2=m₂∙μ_W(πs₂’)=6∙107,32∙64=41210 H

Р_и3=m₃∙ μ_W(πв’)=9∙107,32∙39=37669 H

Р_и4=m₄∙ μ_W(πs₄’)=3,5∙107,32∙78=29298 H

Р_и5= m₅∙ μ_W(πf’)=9∙107,32∙66=63748 H

Положение №8

Р_и1=0

Р_и2=m₂∙ μ_W(πs₂’)=6∙107,32∙44=28332 Н

Р_и3=m₃∙ μ_W(πв’)=9∙107,32∙13=13090 Н

Р_и4=m₄∙ μ_W(πs₄’)=3,5∙107,32∙44=16527 Н

Р_и5=m₅∙ μ_W(πf’)=9∙107,32∙21=20283 Н

Результирующие сил инерции проходит через полюсы инерции τ2 и τ4 шатунов, положение которых определяется отрезками.

3.3 Определение сил тяжести звеньев.

G₁=0

G₂=m₂∙g=58,8 H

G₃=m₃∙g=88,2 H

G₄=m₄∙g=34,3 H

G₅=m₅∙g=88,2 H

3.4 Определение давления в кинематических парах.

3.4.1 Pассмотрение равновесия двухповодковой группы звеньев 4 и 5 (положение 4).

Действующие на группу силы:

Р5=42003 Н – давление газов на поршень F/

Gi – силы тяжести.

Pи – силы инерции.

- давление направляющих на ползун F и давление шатуна 2 на шатун 4.

Условие равновесия группы 4, 5.

где G₄=34,3 Р_и5=63748

Р_и4=29298 Р₅=42003

G₅=88,2 R₀₅= 2125

R₀₅ находится из уравнения моментов всех сил действующих на группу относительно точки С.

Положение №4 .

ΣМ_F=0

3.4.2 Равновесие двухповодковой группы 2,3 (положение №4)

3.4.3 Равновесие кривошипа (положение №4)

3.4.5 Равновесие двухповодковой группы 2,3 (положение №8)

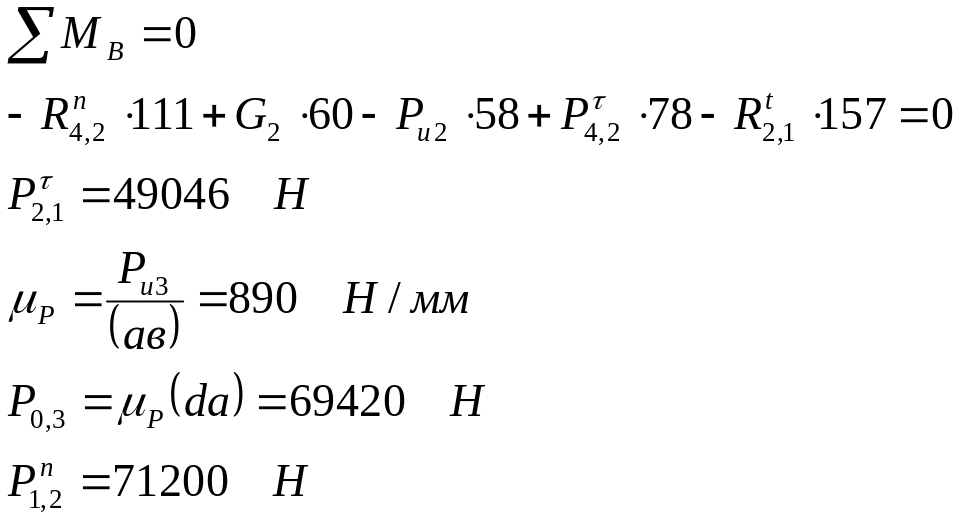
3.4.6 Равновесие кривошипа (положение №8)

3.4.7 Проверка (положение №8)

4. Синтез зубчатого привода.

а) Синтез рядовой зубчатой передачи: z₁=12; z₂=24; m_I=2,5 мм; – исходные данные.

ξ₁=0,706; ξ₂=0,333; ψ=0,17 ([1], стр 64-67)

Сумма коэффициента смещения:

ξ_с=ξ₁+ξ₂=0,706+0,333=1,039

Сумма зубьев: z_c=z₁+z₂=12+24=36

Коэффициентные отношения мелиценперенных расстояний:

a=ξ_с- ψ=1,039-0,17=0,869

Угол зацепления: 1000 ξ_c/z_c=26,64; α_W=26º25´ ([1], стр 29, рис.26)

Радиусы делительных окружностей

Радиусы основных окружностей.

r_в1=r₁∙Cos α₀=15∙Cos 20º=14,1 мм.

r_в2=r₂∙Cos α₀=30∙Cos 20º=28,2 мм.

Радиусы начальных окружностей.

r_W1=r_в1(1+2а/z_c)=15(1+2∙0,87/36)=15,7 мм.

r_W2=r_в2(1+2а/z_c)=30(1+2∙0,87/36)=31,5 мм.

Межцентровое расстояние.

А=m(z_c/2+a)=2,5(36/2+0,87)=47,2 мм.

Радиусы окружностей впадин.

Глубина захода зубьев

Высота зуба.

Радиусы окружностей выступов

r_a1=r_f1+h=13,64+5,21=18,85 мм.

r_a2=r_f2+h=27,71+5,2=32,92 мм.

Шаг зацепления

P=π∙m_I=3,14∙2,5=7,85 мм.

Толщина зуба

S₁= P/2+2ξ₁∙m_I∙tg α₀=7,85/2+2∙0.706∙2,5∙ tg 20°=5,21 мм.

S₂= P/2+2ξ₂∙m_I∙tg α₀=7,85/2+2∙0.333∙2,5∙ tg 20°=4,54 мм.

Сделаем проверку:

r₁+r₂=A 15,7+31,5=47,2

A-r_a1-r_f2=0,25m=0,75 47,2-18,85-27,70=0,65

A-r_a2-r_f1=0,25m=0,75 47,2-32,92-13,64=0.65

Вычислим коэффициент k

k=50/h=50/5,21=9,59=10 масштаб увеличиваем в 10 раз, тогда.

r₁=150 мм. r₂=300 мм.

r_в1=178 мм. r_в2=282 мм.

r_W1=157 мм r_W2=315 мм.

r_f1=136 мм. r_f2=277 мм.

r_a1=189 мм. r_a2=329 мм.

S₁=52 мм. S₂= 45 мм.

А=472 мм; h_зак=46 мм; h=52 мм.

P=79 мм.

Вычислим коэффициенты относительного скольжения.

U₂₁=z₁/z₂=0.5

U₁₂=z₂/ z₁=2

λ₁=1+U₂₁-U₂₁∙g/g-x=1+0,5-0,5*9,81/9,81-x=1,5-4,905/9,81-x

λ₂=1+U₁₂-U₁₂∙g/x=3-19,62/x

xi	0	20	40	60	80	100	120	140	160	180	203
λ1	1	0,95	0,88	0,79	0,67	0,51	0,28	0	-0,86	-2,91	-∞
λ2	-∞	-17,3	-7,15	-3,77	-2,08	-1,06	-0,38	0	0,46	0,74	1

С учетом коэффициента k.

xi	0	20	40	60	80	100	120	140	160	180	203
λ1	20	19	18	16	13	10	6	0	-17	-58	-∞
λ2	-∞	-346	-143	-75	-42	-21	-8	0	9	15	20

Б) Синтез соосного цилиндрического планетарного редуктора.

Z1:z2:z3:c= 1:0,12:1,23:0,74;

проверила условия собираемости:

z₁+z₃=KC

C=(z₁+z₃)K=(140+174)/3=104,67 - условие собираемости выполняется

d₁=m∙z₁=560 мм. d_ω1=d₁=560 мм.

d₂=m∙z₂=68 мм. d_ω2=d₂=68 мм.

d₃=m∙z₂=696 мм. d_ω3=d₃=696 мм.

r₁=280 мм. (140 мм)

r₂=34 мм. (17 мм)

r₃=348 мм. (174 мм)

Масштаб.

μ_v=υ_A3,4/100=86,45/100=0,86 м/с/мм

μ_n=n₁/(KH)=2950/7=421 об/м∙мм.