МІНІСТЕРСТВО ОСВІТИ, НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ АВІАЦІЙНИЙ УНІВЕРСИТЕТ

КАФЕДРА БІОКІБЕРНЕТИКИ ТА АЕРОКОСМІЧНОЇ МЕДИЦИНИ

Домашня робота

З дисципліни: «Техніка експериментальних досліджень»

На тему: «Аналіз даних ЕЕГ – сигналів для інтерфейсів мозок – комп’ютер за допомогою спектрів вищих порядків»

Виконала:

студентка групи ІАСУ 513М

Сковрига О. І.

Перевірив:

асистент Булигіна О. В.

Київ – 2012

Зміст

1.Спектри вищих порядків для аналізу ЕЕГ сигналів інтерфейсів мозок- комп’ютер.

1.1.Спектри вищих порядків.

1.2. Зсув і дисперсія алгоритму оцінювання.

1.3. Переваги, які дає HOSA - аналіз для дослідження ЕЕГ сигналів мозок – комп’ютер.

2. Збір даних. Опис методики та виконання експерименту.

2.1. 1 – й тип: блок даних по двом змінним.

2.2 2 – й тип: блок даних дійсних і уявних рухів (4 змінних).

3.Побудова біспектру для даних ЕЕГ лівої і правої руки.

3.1.Оцінювання семіінваріантів.

3.2. Оцінювачі на основі критеріїв

3.3. Квадратичний фазовий зв’язок

4. Дослідження та аналіз сигналів уявних рухів.

5. Побудова біспектру із застосуванням функції для оцінки зведених статистик та побудови біспектру.

5.1. Застосування функції пошуку статистик до даних ЕЕГ лівої і правої руки.

5.2. Застосування функції пошуку статистик до ЕЕГ сигналу уявного руху правої руки назад.

5.3. Застосування функції пошуку статистик до ЕЕГ сигналу уявного руху лівої руки назад.

6. Висновки.

7. Література.

1.Спектри вищих порядків для аналізу еег сигналів інтерфейсів мозок- комп’ютер

1.1.Спектри вищих порядків

Очевидно, що на практиці безпосередньому виміру піддаються середні відвипадкові величини або середні від їх функцій, тобто деякі моментні функції. Кумулянти ж, як показують співвідношення , які, з точки зору обчислення їх на практиці, можуть бути прийняті в якості визначення кумулянтів, для свого виміру вимагають відповідно додаткового, і в загальному випадку великого,числа моментів нижчих порядків. Що ж тоді спонукає нас при описі випадкових величин чи процесів дозволити підхід, заснований на аналізі їх кумулянтів перед методом,характеризує випадкові величини послідовністю їх моментів. Щоб відповісти на це питання необхідно зрозуміти статистичний зміст кумулянтів,що, природно, неможливо без опису їх найбільш загальних властивостей.

Для того щоб охарактеризувати негаусові складові, що містяться в ЕЕГ сигналах, був запропонований новий метод знаходження статистичних характеристик заснований на HOSA - аналізі, і застосовується для класифікації сигналів ЕЕГ для покращення систем інтерфейсів мозок-комп'ютер, що працюють на основі ЕЕГ.

При статистичному описі фізичних процесів або систем, для яких звичайна характерна кінцева пам'ять про минулі значеннях або станах, корисним, у порівнянні з моментами, є наступна властивість кумулянтів. Якщо випадковий процес X (T) володіє кінцевою довжиною статистичних зв'язків, тобто його значення Х(t1) і X(t2) стають статистично незалежні при | t1 - t2 | , то всякий кумулянт

x(t1),…, x(tn)0 (|tk – tl| ),

Якщо хоча б для однієї пари часових аргументів |tk – tl| . Наприклад,

x[2](t1), x[2](t2)0, при |t1 – t2|,

Тоді як для моменту

x[2](t1) x[2](t2)x[2](t1)x[2](t2)при |t1 – t2|.

Наведені вище міркування, що розкривають статистичний сенс кумулянтів як величин, що характеризують певні статистичні зв'язки і залежності,притаманні конкретним випадковим величинам або процесам, дають нам можливість розглядати кумулянти як ті незалежні елементи, з яких можна побудувати повний статистичний опис даного випадкового явища. Дійсно, з усіх найбільш відомих способів статистичного опису саме при кумулянтному описі окремі його елементи найменш залежні від інших, тому ступінь перекривання інформації, що міститься в різних кумулянтах, найменша.

Автокореляційна функція або послідовність стаціонарного процесу х (n), визначається як: (1-1) де E {.} позначає оператор очікування. Спектр потужності формально визначається як перетворення Фур'є (FT) автокорреляційної послідовності (теорема Вінера-Хінчина) 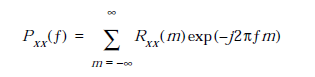(1-2) де f означає частоту. Еквівалентнt визначення: (1-3) де є перетворенням Фур'є х(n) 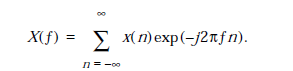(1-4) Достатня, але не обов'язкова, умова існування спектра потужності: автокореляція –така, що може обов’язково бути просумована. Спектр потужності приймає дійсні та невід’ємні значення, тобто якщо х(n) має дійсні значення, то спектр потужності також симетричний, тобто

Як ми побачимо далі, вищі моменти є природним узагальненням автокореляції і кумулянти - конкретні нелінійні комбінації цих моментів. Першого порядку кумулянти стаціонарного процесу є середнім, C1x := E{x(t)}. Вищих порядків кумулянти - інваріантні до зсуву середнього, отже, зручно визначити їх в припущенні нульового середнього, якщо процес має ненульове середнє, значить, ми віднімаємо середнє, а потім застосовуємо такі визначення до результуючого процесу. Другого, третього і четвертого порядків семі інваріанти з нульовим середнім стаціонарним процесом визначаються в [4]. C2xk= Ex*nxn + k

C3xkl= Ex*nxn + kxn + l

C4xklm= Ex*nxn + kxn + lx*n + m

– C2xkC2xl – m– C2xlC2xk – m

– mM2xk – l

де M2x(m) = E{x(n) x(n + m)} і дорівнює C2x(m), для процесу, що має дійсні значення. Першого порядку кумулянти є середнім арифметичним процесу та другого порядку кумулянти є автоковаріаційними послідовностями. Зазначимо, що для складних процесів, є кілька способів визначення кумулянтів залежно від того, що поєднане. Кумулянти з нульовою затримкою мають спеціальні назви: C2x(0) - дисперсіїя і звичайно позначається C3x(0,0) і C4x(0,0,0) як правило, позначаються і Ми будемо називати нормовані величини: - асиметрією, - ексцесом. Ці нормованої величини - одночасно інваріанти і зсуву і масштабу. Якщо x(n) симетрично розподіленй, його ассиметрія обов'язково рівна нулю (але не навпаки), якщо x(n) - має гаусовий розподіл, його ексцес обов'язково рівний нулю (але не навпаки). Часто терміни асиметрії та ексцесу використовується для позначення ненормованих величин і . Якщо х (n) є i.i.d. процеси його кумулянтов відмінні від нуля лише в початку координат. Якщо х (n) статистично не залежить від y(n), і z(n) = x(n) + y(n), то

C4zklm= C4xklm+ C4yklm з подібними зв’язками для кумулянтів всіх порядків. Це властивість адитивності спрощує аналіз, що базується на кумулянтах.

Кумулянти стаціонарних, дійсних значень процесів є симетричними в своїх аргументах, тобто

C2xk= C2x–k

C3xkl= C3xlk= C3x–kl – k

C4xklm= C4xlkm= C4xkml= C4x–kl – km – k

Таким чином, фундаментальна область значень -це не вся k-D площина. Наприклад, для к = 2, C2x(k), k 0, визначає C2x(k) у всьому світі. Легко показати,що ненадлишковиа область C3x(k,l) є клином

А для це конус

Поліспектр к-го порядку визначається як перетворення Фур’є відповідної кумулянтної послідовності:

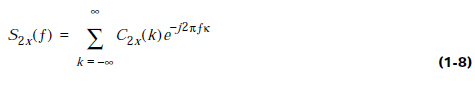
Які, відповідно спектром потужності, біспектром та триспектром. Зверніть увагу, що біспектр є функцією двох частот, в той час як триспектр є функцією трьох частот. На відміну від спектру потужності, який є спектром дійсних значень , да додатнім, біспектр та триспектр є спектрами комплексних значень.

Для процесу,що приймає дійсні значення, симетричні властивості кумулянтів переходять у симетр. властивості поліспектру. Спектр потужності – симетричний: Симетричні властивості біспектру подані в [56]:

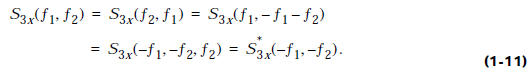
Отже, не надлишкова область значень буспектру це трикутник з векторів (0,0), (1/3,1/3) and (1/2,0); нагадаємо, що ми прийняли нормалізовану частоту дискретизації 1 Гц.

Властивості симетрії триспектру включають в себе:

Література є дещо незрозумілою як в доведенні, так і в Ооисі ненадлишкових областей. Ненадлишкові області, для процесів, які постійні за часом, з обмеженою смугою пропускання, з частотою Найквіста 0,5 Гц, є трикутниками з вершинами (0,0), (1/4, 1/4), (1/2, 0). Посібник з відмінностей між випадками безперервними за часом і дискретними за часом дається в [47], пов'язані обговорення можна знайти в [63]. Ненадлишкові області триспектру обговорюється в [6, 9, 47].

Подібно до крос-кореляції, ми можемо також визначити поперечні кумулянти, наприклад,

Поперечний біспектр визначається

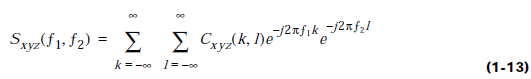
Зверніть увагу, що біспектр є окремим випадком поперечного біспектру отриманого за умови х = у = Z.

Поперечна бікогерентність - інша прикладна статистика, яка визначається як

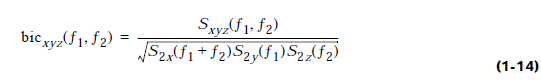
 квадратичний нормалізований біспектр

Наприклад, біспектр , ф перетворення та комплексна згортка, недостатньо спроможна оцінка

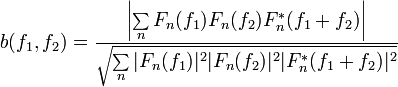(Sigl & Chamoun 1994)

В фізиці плазми використовують

Найбільш прийнятна формула (Hagihira 2001 and Hayashi 2007):

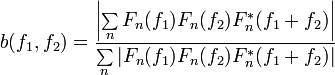
Автобікогерентність отримується, коли х = у = Z. М-файл bicoherx може бути використаний для оцінки поперечної бікогерентності та когерентності.

Поперечна бікогерентність з трьох процесів визначається

і є коректним, тільки якщо відмінней від нуля в усьому діапазоні.

Навіщо потрібні статистики вищого порядку?

Причиною використання кумулянтів і поліспектру порядку к> 2 дається наступним виразом (mk = (m1 . . . , mk-1)):

• Якщо z(n) = x(n) + y(n), і x(n) and y(n) є незалежними один від одного

процесами, то

• Якщо x(n) є гауссовським, то

• Таким чином, якщо z(n) = x(n) + w(n), де w(n) є гауссовським і не залежним від x(n) то для к> 2, . Таким чином, ми можемо відновити більш високого порядку кумулянти негауссовського сигналу навіть за наявності кольорового гаусівсбкого шуму.

• Нехай x(n) є лінійним процесом, тобто де u(n) – це i.i.d. процес. Тоді, випливає, що:

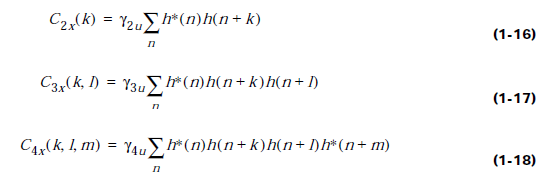
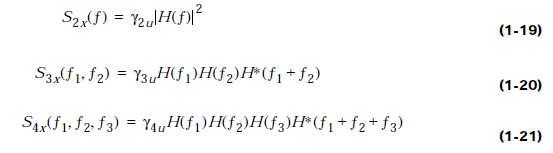
Де Зауважимо, що спектр потужності не несе жодної інформації про фазу H(). Напротивагу, якщо u(n) – не гаусів, то ця інформація про фазу може бути відновлена зі поліспектру вищих порядків. Таким чином, стандартне мінімально-фазове припущення, яке необхідне, коли процес гаусів або статистики тільки другого порядку, які використовуються, можуть бути видалені.

• Будь-який процес завжди можна розглядати як лінійний процес щодо його статистик другого порядку, тобто, враховуючи , ми завжди зможемо знайти і некорельований процес u(n), такий що, де

Іншими словами, автокореляційна послідовність не може дати жодних доказів нелінійності. І навпаки, кумулянти більш високого порядку можуть говорити про нелінійність.

• Процеси вигляду , де фаза - многочлен часу t, називаються поліноміальними процеси фази; перетворення Фур’є таких процесів, як правило, прямі лінії, в той час як визначені відповідно частини спектру вищого порядку дають структуру, що дозволяє оцінити р і Підводячи підсумок, кумулянти є зручними:

1. якщо адитивний шум є гаусовим, а сигнал - ні,

2. лінійна система не є мінімально фазовою (тобто, змішаної фази), або

3. процес носить нелінійний характер.