5. Графики изменения основных элементов траектории

Рис.4.1. График зависимости скорости от времени.

Рис.4.2 График зависимости угла наклона от времени.

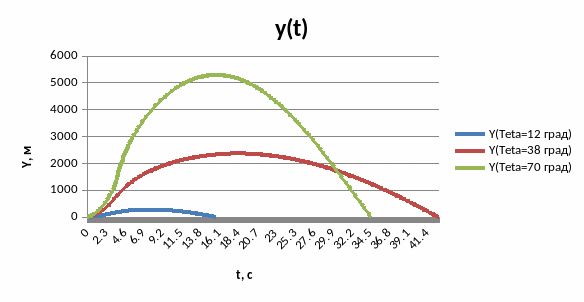
Рис.4.3. График зависимости координаты Y от времени

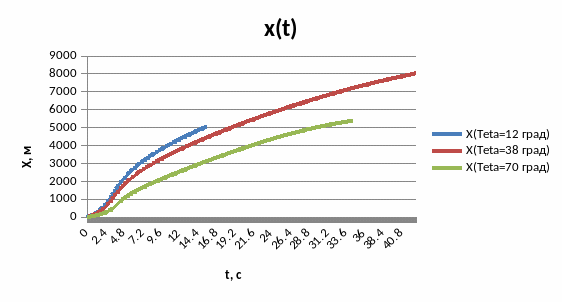
Рис.4.4 График зависимости координаты Х от времени.

Рис.4.5 График зависимости скорости от координаты Х.

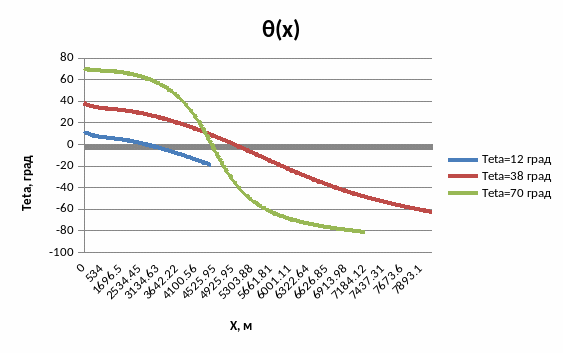
Рис.4.6. График зависимости угла наклона траектории от координаты Х

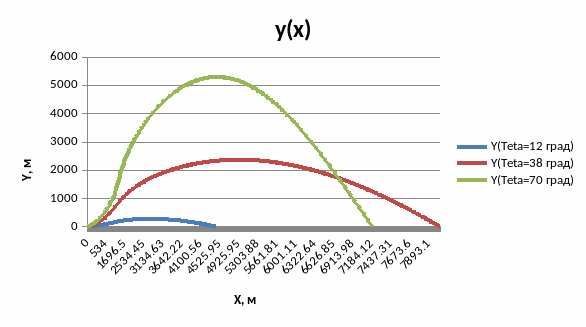
Рис.4.7. Траектория

6. Методы определения угла максимальной дальности и угла бросания, обеспечивающего заданную дальность.

Определение угла максимальной дальности может осуществляться различными методами. В работе мы использовали метод половинных отрезков - разделение отрезка пополам и вычисление значений функций от середин двух полученных отрезков, затем аналогичное разбиение с тем значением, которое оказалось больше.

Описание метода половинного деления

Метод половинного деления – один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до того времени, пока не будет достигнута заданная точность Е. Метод используется при решении квадртных уравнений и уравнений высших степеней.

Пусть задан отрезок [а,b], содержащий один корень уравнения. Этот отрезок может быть предварительно найден с помощью шагового метода.

Алгоритм метода половинного деления

• Определить новое приближение корня х в середине отрезка [а,b]: х=(а+b)/2.

• Найти значения функции в точках а и х: F(a) и F(x).

• Проверить условие F(a)*F(x) < 0. Если условие выполнено, то корень расположен на отрезке [а,х]. В этом случае необходимо точку b переместить в точку х (b=х). Если условие не выполнено, то корень расположен на отрезке [х,b]. В этом случае необходимо точку а переместить в точку х (а=х).

• Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм продолжить до того времени, пока не будет выполнено условие /F(x)/ < e.

Рис. 6.1. Иллюстрация метода половинного деления

Достоинство метода половинного деления: более быстрая сходимость к заданной точности, чем у шагового. Недостаток: если на отрезке [а,b] содержится более одного корня, то метод не работает.

Таблица 5.1. Определение угла максимальной дальности

Teta, град	X,м
45	4710.558
43.5938	4729.695
42.89065	4736.163
42.5391	4738.642
42.1875	4740.594
41.4844	4742.308
41.1328	4743.383
41.1	4743.394
41.05	4743.406
41	4743.412
40.957	4743.399
40.78125	4743.308
40.4297	4742.693
40.0781	4741.568
39.375	4737.795
33.75	4633.467
22.5	4016.932

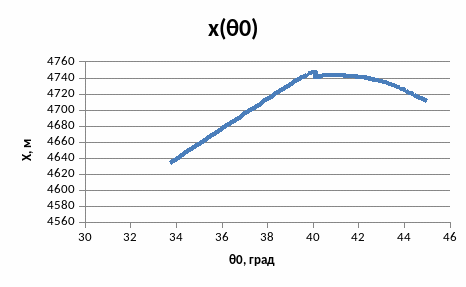
Рис.5.1. График зависимости x(₀)

Таблица 5.2. Определение угла бросания, обеспечивающего дальность х_к = 3000 м

Teta1, град	X,м		Teta2, град	X,м
45	4710.558		70	2998.12
22.5	4016.932		69.98	3000.51
16.875	3484.350		69.985	2999.91
14.0625	3151.871		69.98425	3000.00
13.3594	3060.911		69.984	3000.03
13.00785	3014.171
12.919975	3002.428
12.91	3001.002
12.905	3000.328
12.904	3000.195
12.903	3000.060
12.9026	3000.006
12.90257	3000.000
12.898	2999.387
12.876	2996.428
12.8321	2990.486
12.6563	2966.564
11.25	2767.017

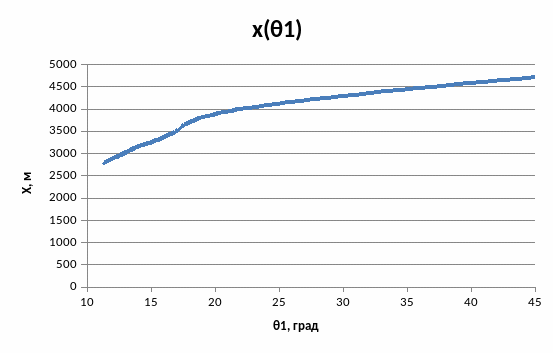
Рис.5.2. График зависимости x(₁)

Рис.5.3. График зависимости x(₂)