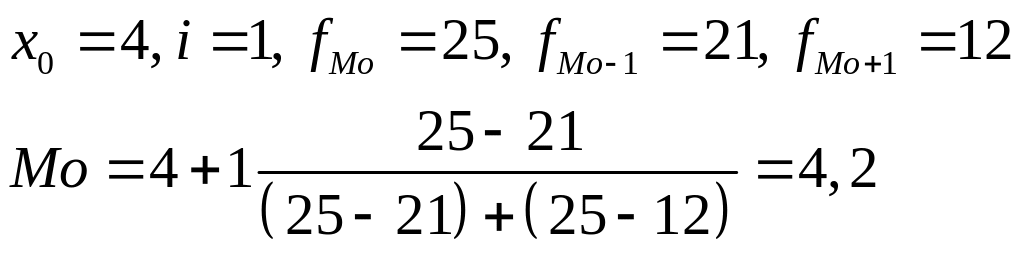Показатели вариации

Величины признаков статистической совокупности колеблются или варьируют под действием причин или признаков, которые называют – факторами.

Например, вариация оценок студентов на экзамене вызывается:

- различными способностями студентов

- временем на подготовку существенный фактор

- посещаемостью

- временные недомогания – случайный фактор.

Вариация, порождаемая существенными факторами, называется – систематической. Вариация, обусловленная случайными факторами, называется – случайной вариацией.

Мы будем иметь дело со случайной вариацией.

Совокупность значений изучаемого признака с указанием числа различных значений из распределения признака.

В процессе анализа распределения признака необходимо рассчитать различные числовые характеристики – показатели.

Все показатели вариации можно разделить на 3 группы:

1. Показатели центра распределения – средняя арифметическая, мода, медиана;

2. Показатели степени вариации – вариационный размах, среднее линейное отклонение, среднее квадратичное отклонение и коэффициент вариации;

3. Показатели формы распределения – структурные характеристики, показатели асимметрии и эксцесса, кривые распределения.

Показатели центра распределения

Средняя арифметическая нами уже была рассмотрена.

Мода это такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто.

Например, рабочие одной бригады из 11 человек имеют следующие разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5 – это не сгруппированные данные. Здесь чаще всего встречается 5-ый разряд, .

Теперь рассмотрим упорядоченное дискретное распределение:

Группы рабочих по тарифному разряду, x	Численность рабочих, f	Накопление частот
2 3 4 5 6	20 50 60 70 15	20 70 130 20 215
	215

Здесь ищем вариант с наибольшей частотой

Если имеем интервальный ряд, то модальный интервал определяется по наибольшей частоте.

Распределение банков по сроку функционирования

Группы банков по сроку функционирования лет, x	Число банков % к итогу, f	Накопленние частот
1 – 2 2 – 3 3 – 4	10 15 21	10 25 46
4 – 5	25	71
5 – 6	12	83
6 – 7	7	90
7 – 8	5	95
свыше 8	5	100
	100

Мода определяется по формуле:

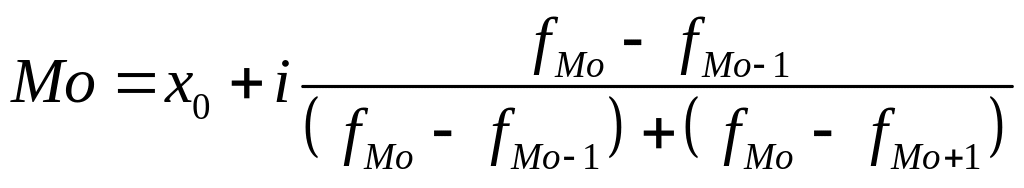
нижняя граница модального интервала;

величина модального интервала;

частота модального интервала;

частота интервала, предшествующего модальному;

частота интервала, следующего за модальным.

(4 – 5) – модальный интервал

25