Построение статистических группировок

Для построения статистической группировки необходимо:

- выбрать группировочный признак;

- затем число групп и зафиксировать границы интервалов групп;

- для каждой группировки найти затем, которые должны характеризовать группы.

Группировочный признак называют еще основанием группировки. Основание группировки может быть как количественным, так и качественным.

При группировке по количественному признаку количество групп зависит от того, насколько сильно колеблется признак. Чем сильнее, тем больше число групп нужно образовывать.

Для определения оптимального количества групп применяется формула Стерджесса:

N – число единиц совокупности;

n – число групп.

Эта формула хороша для большой совокупности и распределение близко к нормальному.

N = 1000

Также для определения числа групп применяется способ, основанный на среднем квадратичном отклонении СО.

После определения числа групп необходимо определить интервал группировки с верхней и нижней границами и шириной.

Интервал может быть равным и неравным.

Ширина равного интервала определяется по формуле:

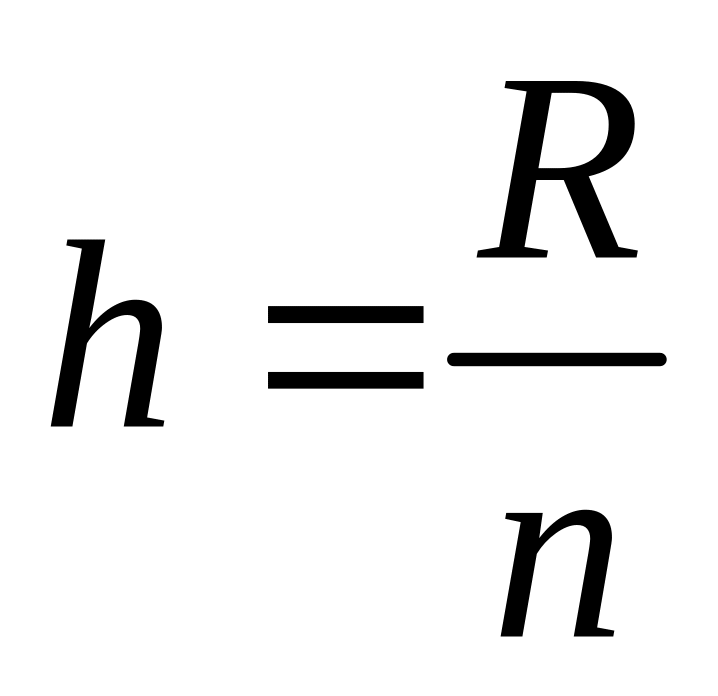
– размер вариации ;

– максимальное и минимальное значение признака;

n – число групп.

Пример: имеют данные о стоимости основных фондов предприятия.

Максимальное значение – 2040 млн. руб., минимальное – 290 млн. руб.

Совокупность включает в себя 80 ед.

Формула Стерджесса:

R = 2040 – 290 = 1750 млн. руб.

млн. руб.

Итог:

I – 290 – 540 млн. руб.

II – 540 – 790

….

1790 – 2040

Ряды распределения группировки

После определения группировочного признака и границ групп, строится ряд распределений.

Ряд распределения в статистике – это ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку.

Ряд распределения состоит из двух элементов:

- варианты – групп;

- частоты – численность групп.

Частоты, выраженные в виде относительных величин (%) – называются частностями.

Сумма всех частот называется – объемом распределения.

В общем виде ряд распределения строится так.

Имеется совокупность из N единиц, некоторая переменная величина X (признак) принимает различные значения . Каждое из значений имеет частоту .

Ряд распределения можно представить в следующем виде:

Вариант x	Частота f
x1 x2 … xn	f1 f2 … fn

Распределение семей по числу детей в..

Группы семей по числу детей, x	Число семей		Накопленная частота, S
	тыс. f	% к тыс., W
0	6	5,9	6
1	28	27,5	34
2	22	21,6	56
3	20	19,6	76
4	13	12,7	89
5	8	7,8	96
6	5	4,9	102
	102	100

x – значения признака – варианты, графа тыс. – f – частоты, % - частности,

- накопления частоты.

Это пример дискретного ряда распределения.

Рассмотрим интервальный ряд распределения. Здесь группировочный признак принимает любые значения в определенном интервале.

Распределение семей по размеру жилплощади,

приходящейся на одного человека

Группы семей по размеру жилплощади на 1 человека, x м2	Число семей с данными размерами жилплощади, f	Число семей S
3 – 5	10	10
5 – 7	20	30
7 – 9	30	60
9 – 11	46	100
11 – 13	15	118
	115

Здесь интервалы имеют одинаковую длину.

Если интервалы не равные, то частоты в разных интервалах несопоставимы. Для этого, чтобы частоты можно было сравнивать, вычисляют плотность распределения.

Распределение действующих банков по величине УК

на 01.07.2001 г.

Группы банков по величине УК, млн. руб. x0	млн. руб. ni	Число банков f0	Плотность распределения
1 – 3	2	150	75
3 – 10	7	254	36,3
10 – 30	20	316	15,8
30 – 60	30	256	8,5
60 – 150	90	144	1,6
150 – 300	150	90	0,8
300 – 600	300	112	0,32
		1322

- абсолютная плотность распределения

Относительная плотность

- ряд

Графическое изображение рядов распределения

Графическое изображение облегчает анализ ряда распределения.

Для этого применяются: полигон, гистограмма, кумулята кривая Лоренца.

Полигон используется для изображения дискретных рядов распределения.

Распределение детей:

Гистограмма используется для изображения интервального ряда. Это столбики с основанием, равной ширине интервала, а высота соответствует частоте:

Жилплощадь

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ

Статистические графики позволяют наглядно представить статистические показатели, которые становятся более понятными, выразительными, запоминающимися.

По форме графики делятся на:

- линейные – (статистические кривые)

- плоскостные (столбиковые, полосовые, квадратные, круговые, секторные)

- объемные

По способу построения графики делятся на:

- диаграммы

- статистические карты.

Диаграммы сравнения

Один из видов диаграммы сравнения – это столбиковые диаграммы. Они представляют собой графическое изображение статистических показателей в виде столбиков- прямоугольников. Эти диаграммы используются для наглядного сравнения объектов во времени и пространстве, и для изображения структуры явлений.

Для построения столбиковых диаграмм необходимо начертить систему прямоугольных координат, в которой расположатся столбики. На горизонтальной оси располагаются основания столбиков. Размер основания может быть произвольным, но одинаковым для всех столбиков.

Пример. Динамика численности научных работников региона.

Год	1997	1998	1999	2000	2001	2002	2003
Тыс. чел.	1943,4	1677,8	1532,6	1315,0	1106,3	990,7	860,8

Возьмем систему прямоугольных координат. На оси абсцисс на одинаковом расстоянии нанесем 7 отрезков равной длины. Это будут основания для столбиков. Высота столбиков определяется в соответствии со значениями показателей.

Если взять единичный отрезок на оси ординат, соответствующий 500 тыс. человек, то получим высоту для первого столбика – 3,89, 2-го – 3,36 и т.д.

Здесь наглядность диаграммы достигается сравнением высоты столбиков.

Столбиковые диаграммы также удобно применять для сравнения нескольких показателей.

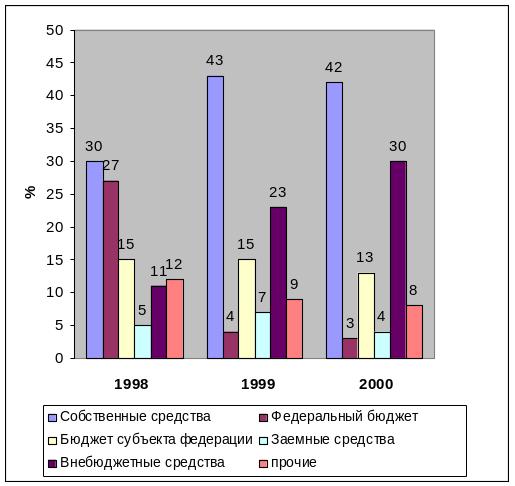
Например, динамика удельного веса финансирования инвестиций в основной капитал за 1999 – 2000 года:

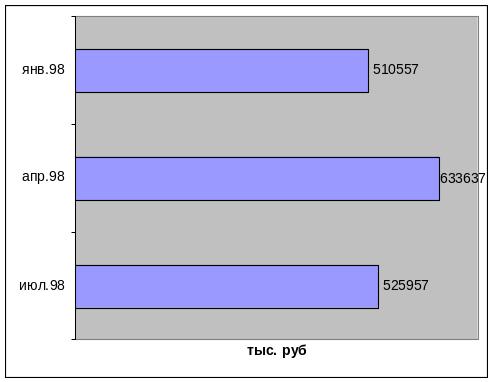
Если столбики повернуть на 90 градусов, те числовые характеристики показателей откладывать по оси абсцисс, то получим ленточные или полосовые диаграммы.

Динамика выдачи кредитов банком России

Столбиковые и полосовые диаграммы используются для характеристики состава совокупности.

Структурные диаграммы

Структурные диаграммы используются для наглядной иллюстрации структуры какого-либо явления, характеристики удельных весов отдельных частей целого.

В качестве графического образа используются прямоугольники и круги. При этом круг используется для сравнения площади отдельных секторов. Это секторная диаграмма. Удельный вес каждой части характеризуется величиной центрального угла, где 360 градусов – это 100 % и 1 % - 3,6 градуса.

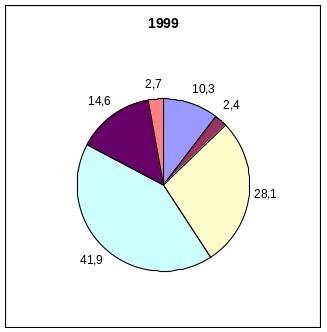
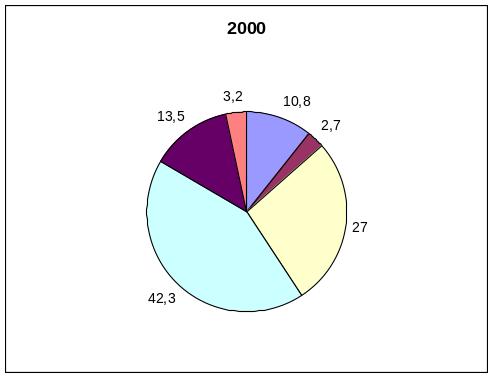
Динамика структуры безработных РФ

по уровню образования за 1999 – 2000 года

Образование	1999	2000
Высшее	10,3	10,8
Незаконченное высшее	2,4	2,7
Среднее профессиональное	28,1	27,0
Среднее полное	41,9	42,3
Основное общее	14,6	13,5
Не имеет основного общего	2,7	3,2
Всего	100	100

СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ

Основные виды статистических показателей

Определение. Статистический показатель – это количественная характеристика социально-экономических процессов и явлений в условиях качественной определенности.

Обычно, изучаемые процессы и явления настолько сложны, что их невозможно отразить при помощи одного показателя и используется система статистических показателей.

Так, например, выпуск продукции каким-либо предприятием характеризуется взаимодействием средств производства и трудовых ресурсов. Поэтому для полного описания функционирования предприятию нужно использовать систему из таких показателей, как прибыль, численность персонала, производительность труда, фондовооруженность.

Статистический показатель получается расчетным путем в отличие от статистического признака.

Рассмотрим понятие конкретный статистический показатель. Он характеризует размер, величину изучаемого явления или процесса в данном месте и в данное время. Так, например, стоимость основных фондов ОАО «Ленинградский механический завод» на 01.01.2006 составила 10,3 млрд. рублей.

Другое понятие – показатель-категория, он отражает общие отличительные свойства конкретных показателей без указания места, времени и числового значения. Например, розничный товарооборот предприятий торговли и общественного питания.

Индивидуальные показатели характеризуют отдельный объект или единицу совокупности, например, оборот ОАО «Большой гостиный двор».

Сводные показатели – характеризуют группу единиц совокупности.