Вопрос 3. Оптимальная численность выборки

Размер ошибки выборки прежде всего зависит от численности выборочной совокупности n. При доведении N до n ошибка выборки  =0. Однако это требует увеличения объемов исследований, дополнительных затрат труда и материальных средств.

Определение оптимальной численности выборки основывается на формуле предельной ошибки выборки. Необходимая численность выборки n_х (для среднего значения) и n_ (для доли альтернативного признака) определяется как:

отсюда (12)

отсюда (13)

В случае бесповторного отбора величины (12) и (13) примут следующий вид:

(14)

(15)

Вопрос 4. Малая выборка

Под малой выборкой (МВ) понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности.

К минимальному объему выборки прибегают, когда большая выборка невозможна, или экономически невыгодна (если проведение исследования связано с порчей или уничтожением обследуемых образцов).

Объем малой выборки обычно не превышает 30 единиц, но м.б. до 4-5 единиц.

Первые работы в области теории малой выборки были выполнены английским статистиком В. Госсетом в 1908г. (псевдоним Стьюдент) и продолжены в исследованиях Р. Фишера.

Величина ошибки МВ определяется по формулам, отличным от формул выборочного наблюдения со сравнительно большим объемом выборки (n > 100). Средняя ошибка малой выборки исчисляется по формуле:

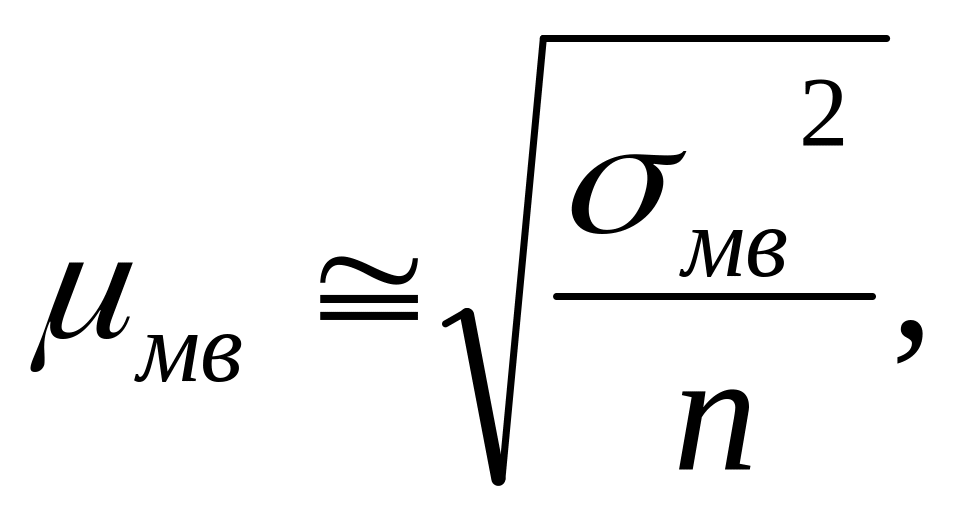где - дисперсия малой выборки. (16)

При МВ величина имеет существенной значение, поэтому вычисление дисперсии малой выборки проводится с учетом числа степеней свободы.

Число степеней свободы – это количество вариантов, которые могут принимать произвольные значения, не меняя величины средней.

При определении дисперсии число степеней свободы = n – 1,

Тогда дисперсия МВ находится по формуле: (17)

Предельная ошибка малой выборки: _мв = t  _мв.

При этом для МВ t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n.

Для отдельных значений t и n доверительная вероятность МВ определяется по таблицам Стьюдента, в которых даны распределения стандартизованных отклонений:

(18)

При увеличении n распределение Стьюдента приближается к нормальному и при

n = 20 оно уже мало отличается от нормального распределения.

Вопрос 5. Распространение характеристик выборки на генеральную совокупность

В зависимости от цели исследования применяются следующих два метода:

1) способ прямого пересчета показателей выборки для генеральной совокупности

2) посредством расчета поправочных коэффициентов.

1. При использовании способа прямого пересчета показатели выборочной доли или средней распространяются на генеральную совокупность с учетом ошибки выборки.

Практическое использование.

Определение в поступившей партии товара нестандартных изделий. Для этого (с учетом принятой степени вероятности) показатели доли нестандартных изделий в выборке умножаются на численность изделий во всей партии товара.

Проводится выборочное обследование поступившей партии хлебобулочных изделий в 2000ед. Количество нестандартных изделий в выборке 100 единиц равно 10.

Вычислена доля нестандартных изделий в выборке w = 10/100=0,1.

Для установленной вероятности = 0,954 подсчитана предельная ошибка выборки

. Тогда доля нестандартных изделий во всей партии составит

или от 0,04 до 0,16.

На основе этих данных численность нестандартных изделий во всей партии:

Минимальная = 2000*0,04=80шт.

Максимальная = 2000*0,16=320шт.

2. способ поправочных коэффициентов применяется, если целью выборочного метода является уточнение результатов сплошного учета:

Практическое использование.

Например, в отечественной практике этот метод используется при уточнении ежегодных переписей скота, находящегося у населения. Для этого после получения данных сплошного учета, практикуется 10%-ное выборочное обследование с определение т.н. «процента недоучета».

Если в хозяйствах поселка по данным 10% - й выборки зарегистрировано 52 головы скота, а по данным сплошного учета в этом массиве значится 50 голов, то коэффициент недоучета составляет 4% (2/50*100=4%)

С учетом полученного коэффициента вносится поправка в общую численность скота, находящегося у населения данного поселка.

Распространение выборочных данных на генеральную совокупность производится с учетом доверительных интервалов. Для этого соответствующие обобщающие показатели выборочной совокупности  и корректируются величиной предельной ошибки выборки ∆_w и :

Для доли альтернативного признака:

Для средней величины количественного признака: