
- •Тема 5-2011-2012. Показатели вариации
- •Вопрос 1. Понятие вариации. Абсолютные и средние показатели вариации
- •Вопрос 2. Показатели относительного рассеивания
- •Вопрос 3. Виды дисперсии
- •Вопрос 4. Анализ данных. Базовые показатели. Блочные диаграммы.
- •Вопрос 5. Дисперсия альтернативного (качественного признака)
Вопрос 4. Анализ данных. Базовые показатели. Блочные диаграммы.
Вычисление показателей с помощью Пакета Анализа
Пятилетняя доходность фондов с высоким уровнем риска |
|
|
|
Среднее |
6,08 |
Стандартная ошибка |
1,709084968 |
Медиана |
6,5 |
Мода |
#Н/Д |
Стандартное отклонение |
6,619257619 |
Дисперсия выборки |
43,81457143 |
Эксцесс |
-0,224739779 |
Асимметричность |
-0,148297869 |
Интервал |
24,6 |
Минимум |
-6,1 |
Максимум |
18,5 |
Сумма |
91,2 |
Счет |
15 |
Наибольший(1) |
18,5 |
Наименьший(1) |
-6,1 |
Стандартная ошибка – стандартное отклонение деленное на квадратный корень объема выборки.
Ассиметричность характеризует отклонение от симметричности распределения и является функцией, зависящей от куба разностей между элементами выборки и средним значением.
Эксцесс – это мера относительной концентрации данных вокруг среднего значения по сравнению с хвостами распределения; зависит от разностей между элементами выборки и средним значением, возведенными в четвертую степень.
Основные характеристики позволяют описать свойства данных и перейти к более глубоким исследованиям. Довольно часто для анализа данных применяется подход, основанный на пятерке базовых показателей и построении блочной диаграммы.
Блочная диаграмма представляет собой удобное средство для изображения пяти базовых показателей:
![]()
Применение понятий
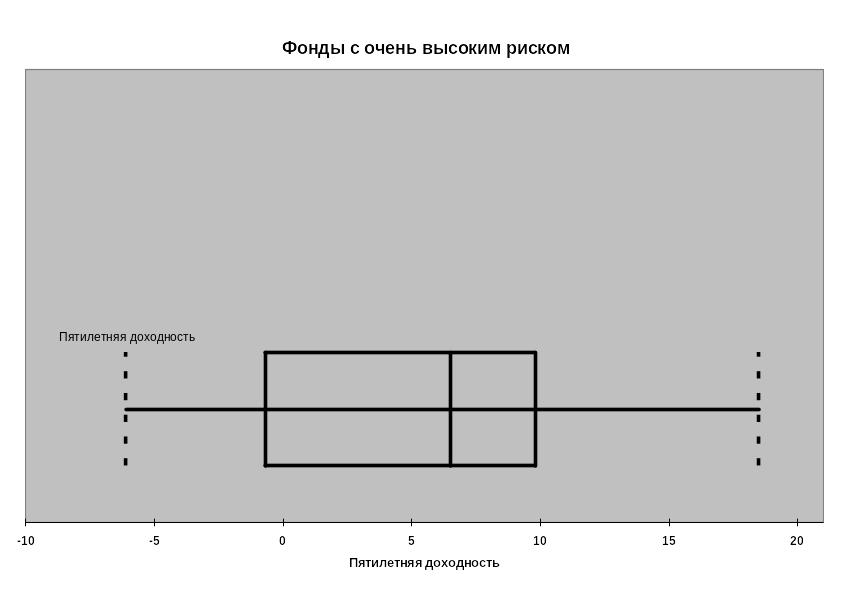
Здесь изображена блочная диаграмма, иллюстрирующая показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска
Вертикальная линия, проведенная внутри
прямоугольника, отмечает медиану. Левая
сторона прямоугольника соответствует
первому квартилю
![]() ,
а правая – третьему квартилю
,
а правая – третьему квартилю
![]() .
Таким образом, прямоугольник содержит
средние 50% элементов выборки. Младшие
25%данных изображаются в виде линии (так
называемый ус), соединяющей левую
сторону прямоугольника с наименьшим
выборочным значением
.
Таким образом, прямоугольник содержит
средние 50% элементов выборки. Младшие
25%данных изображаются в виде линии (так
называемый ус), соединяющей левую
сторону прямоугольника с наименьшим
выборочным значением
![]() .
Следовательно, старшим 25% данных
соответствует линия, соединяющая правую
сторону прямоугольника с наибольшим
выборочным значением
.
Следовательно, старшим 25% данных
соответствует линия, соединяющая правую
сторону прямоугольника с наибольшим
выборочным значением
![]() .
.
Изображение нескольких диаграмм на одном рисунке намного облегчает анализ и сравнение данных
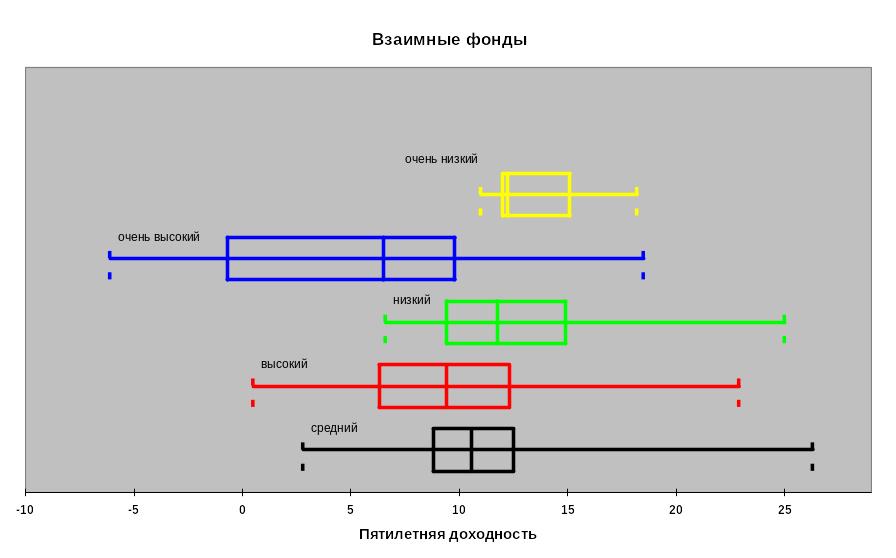
Вывод: чем меньше риск, тем выше эффективность фондов
Вопрос 5. Дисперсия альтернативного (качественного признака)
Альтернативные – это признаки, которыми обладают одни единицы совокупности и не обладают другие.
Наличие изучаемого признака обозначается 1, а его отсутствие 0.
Доля показателей, обладающих изучаемым признаком, обозначается – р, а доля значений, не обладающих признаком, обозначается q.
P + q = 1
Найдем их средние значения и дисперсию.
![]()
![]() =
=
![]()
Применение понятий
10 000 населения. Из них 4000 мужчин 6000 женщин
Р = 4000/10000 = 0,4 q = 6000/10000 = 0,6
![]() р*q
= 0.4*0.6 = 0.24
р*q
= 0.4*0.6 = 0.24
P + q не может быть больше 1, а р*q не может быть больше 0,25
Тогда
=
![]() =
0,49.
=
0,49.
