Исследовательская часть

Исследуем, как будут меняться функции v, y, x, в зависимости от подстановки в уравнения движения неуправляемого летательного аппарата в проекциях на касательную и нормаль к траектории значений коэффициента свободного падения с разной точностью задания (см. табл. 6, 7).

Таблица 6: Расчёт активного участка

	Скорость vа,	Угол θа	Высота yа, м	Дальность xа, м	Время tа, с	Коэф. своб. падения g
Метод Рунге-Кутта	432.42	0.574	552.47	789.37	4	9.81
	432.10	0.569	549.17	790.83	4	10
Метод Эйлера	448	0.575	565.39	807.67	4	9.81
	447.09	0.570	561.19	808.16	4	10

Таблица 7: Расчёт пассивного участка

	Скорость vп,	Угол θп	Высота yп, м	Дальность xп, м	Время tп, с	Коэф. своб. падения g
Метод Рунге-Кутта	237.377	-0.906	0	10426.327	46,488	9.81
	238.600	-0.900	0	10288.818	45.558	10
Метод Эйлера	240.461	-0.914	0	10884.580	47.618	9.81
	241.703	-0.908	0	10744.871	46.668	10

Из таблиц 6 и 7 видно, что изменение величины коэффициента свободного падения g в пределах (9.81 - 10)м/с существенным образом не оказывает влияние на функции v, y, . Изменение коэффициента свободного падения g более существенно влияет только на дальность x.

Исследуем точность метода Рунге-Кутта и метода Эйлера на примере дальности неуправляемого ЛА x_п. Точность в этих методах определяется заданием шага интегрирования . Будем последовательно делить на 2, если точность велика, и последовательно умножать на 2, в случае, если точность удовлетворяет (см.табл.8).

Таблица 8

		Дальность xп, м
Метод Рунге-Кутта	=0.02	10452.093
	=0.01	10426.327
		10426.866
Метод Эйлера	=0.02	10573.747
	=0.01	10884.580
		10885.449

8 видно, что шаг =0.01 выбран верно, т.к. при изменение значения дальности полёта неуправляемого ЛА незначительно, а при =0.10 изменение дальности полёта уже существенно.

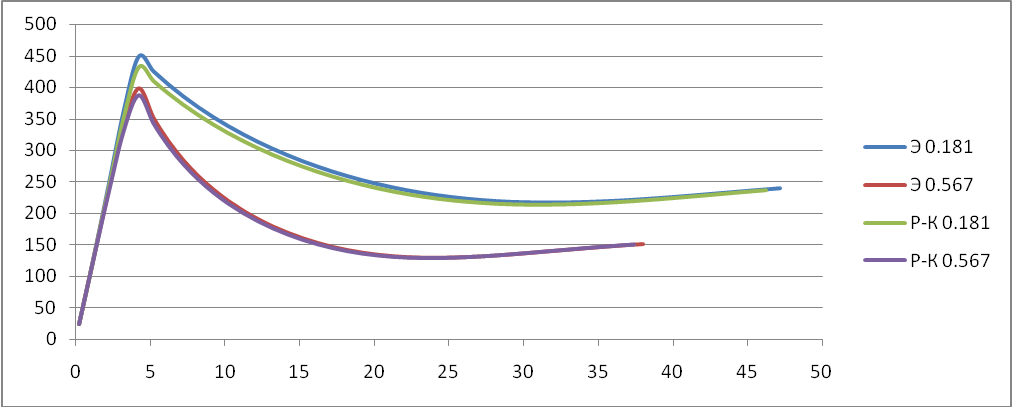
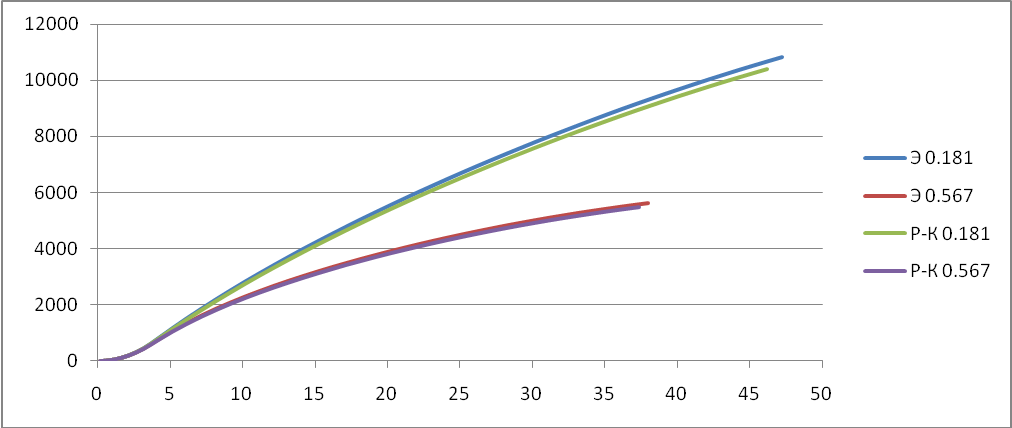
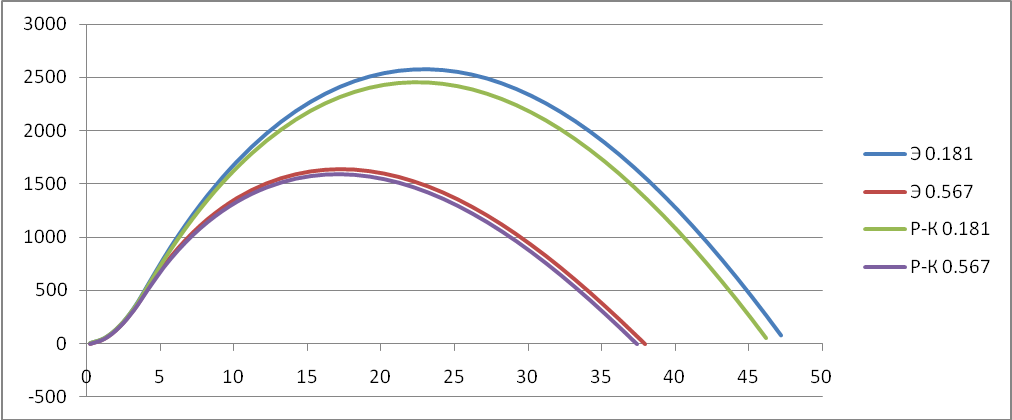
Исследуем поведение функции v, y, x, в зависимости от времени t при постоянном коэффициенте лобового сопротивления Cx. В качестве значений Cx возьмём: 0.157; 0.181; 0.567.

V(t):

C_x=0.157

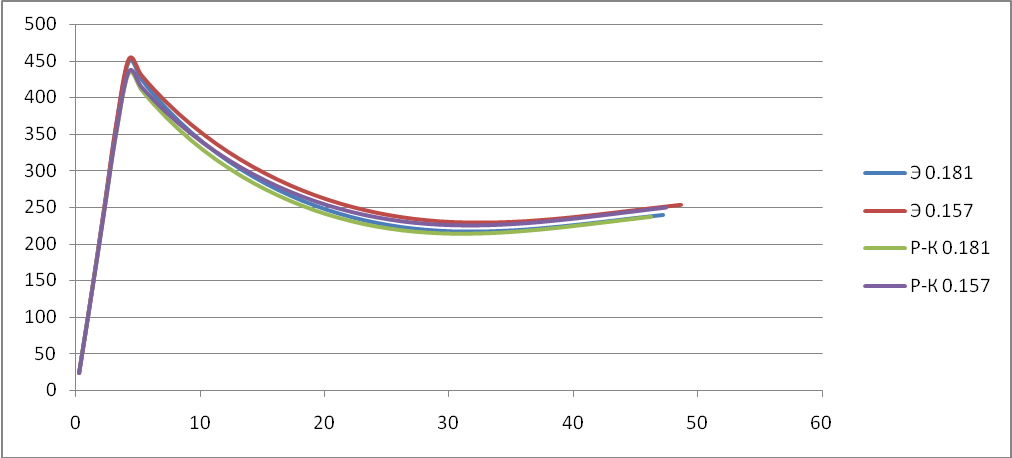
Сх=0.567

Q(t)

C_x=0.157

Сх=0.567

X(t):

C_x=0.157

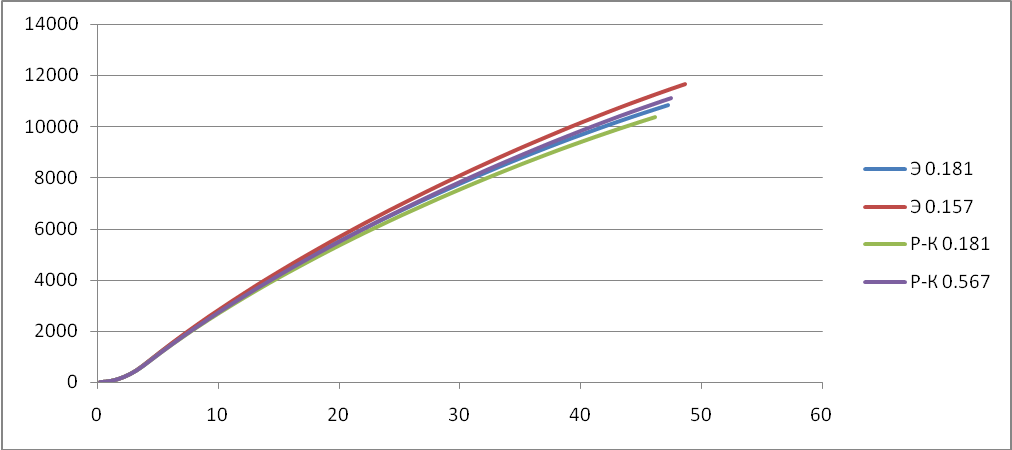
Сх=0.567

Y(t):

C_x=0.157

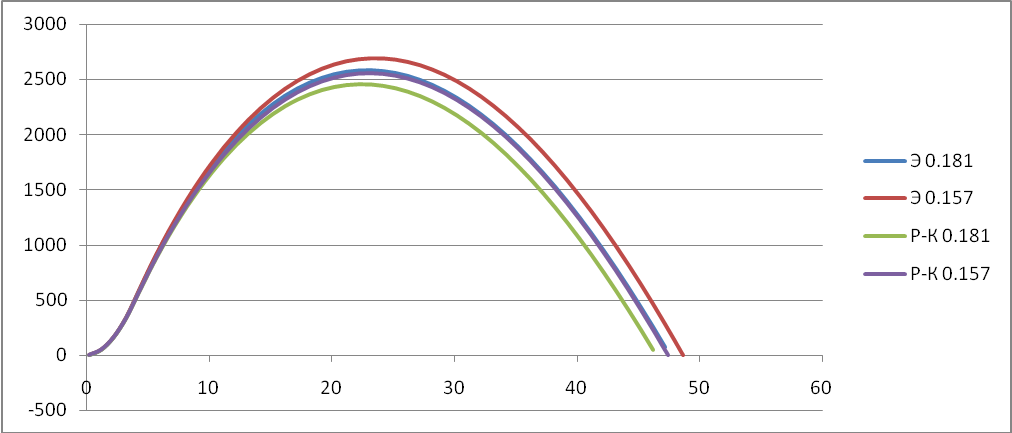
Сх=0.567

Приложение

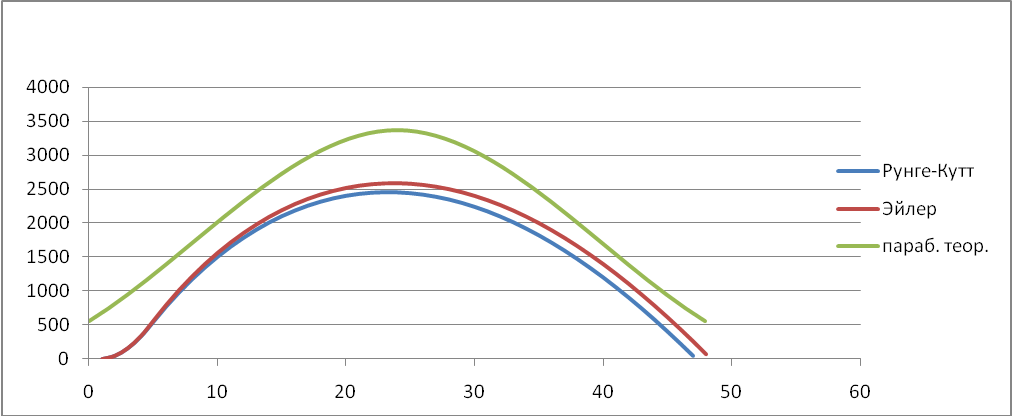
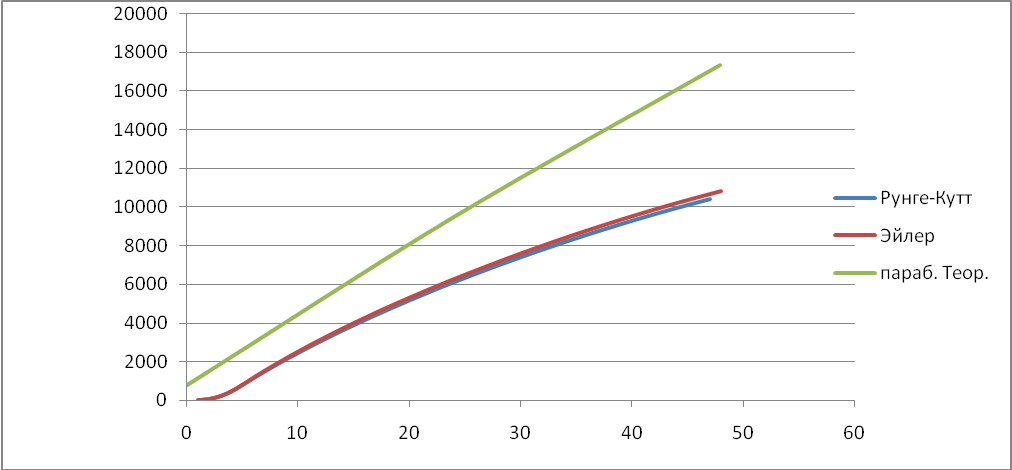
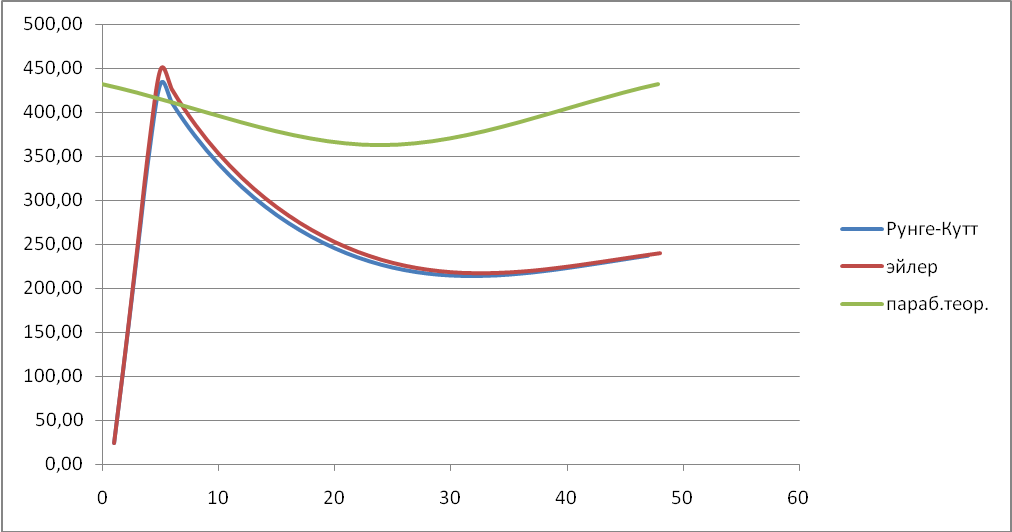
Траектория неуправляемого летательного аппарата

Зависимость y(t)

Зависимость x(t)

Зависимость v(t)

Зависимость угла

Зависимость y(x)

Программа расчета методом Рунге Кутта:

#include<stdio.h>

#include<math.h>

#include<conio.h>

#include<iostream.h>

#include<stdlib.h>

#include<dos.h>

main()

{

FILE *fin;

float t0,v0,y0,x0,dt,cx,i,ay1,ay2,ay3,ay4,r,ay11,ay22,ay33,ay44,

by1,by2,by3,by4,by11,by22,by33,by44,cy1,cy2,cy3,cy4,cy11,cy22,cy33,cy44,

dy1,dy2,dy3,dy4,dy11,dy22,dy33,dy44,q,q0,m,y111,y222,y333,s,y1,y2,y3,y4,w,w1,w2;

int k=1;

clrscr();

printf("PROGRAMMA RASCHOTA RUNGI-KUTT\n");

printf("Vvedite dt=");

scanf("%f",&dt);

printf("Vvedite t0=");

scanf("%f",&t0);

printf("Vvedite v0=");

scanf("%f",&v0);

printf("Vvedite y0=");

scanf("%f",&y0);

printf("Vvedite x0=");

scanf("%f",&x0);

printf("Vvedite cx=");

scanf("%f",&cx);

printf("Vvedite i=");

scanf("%f",&i);

printf("Vvedite q0=");

scanf("%f",&q0);

printf("Vvedite q=");

scanf("%f",&q);

printf("vvedite r=");

scanf("%f",&r);

printf("Vvedite s=");

scanf("%f",&s);

printf("Vvedite m=");

scanf("%f",&m);

printf("CHTOBU NACHAT RASCHOT NAGMITE 'ENTER'\n");

getch();

fin=fopen("RUNGIKUTT.txt","w+");

q0=((M_PI)*q0)/180;

w=m-q*t0; w1=m-q*(t0+dt);w2=m-q*(t0+(dt/2));

do{

if(t0>=2) w=w1=w2=m-q*2;

ay1=(r/w)-(0.5*i*cx*1.24*exp((-y0)/7800)*s*pow(v0,2))/w-9.81*sin(q0);

ay2=(-9.81*cos(q0))/v0;

ay3=v0*sin(q0);

w=m-q*(t0+dt);

by11=v0+ay1*(dt/2);

by22=q0+ay2*(dt/2);

by33=y0+ay3*(dt/2);

by1=(r/w2)-(0.5*i*cx*1.24*exp((-by33)/7800)*s*pow(by11,2)/w2)-9.81*sin(by22);

by2=(-9.81*cos(by22))/by11;

by3=by11*sin(by22);

cy11=v0+by1*(dt/2);

cy22=q0+by2*(dt/2);

cy33=y0+by3*(dt/2);

cy1=(r/w2)-((0.5*i*cx*1.24*exp((-cy33)/7800)*s*pow(cy11,2))/w2)-9.81*sin(cy22);

cy2=(-9.81*cos(cy22))/cy11;

cy3=cy11*sin(cy22);

w2=w2-q*(dt/2);

dy11=v0+cy1*(dt/2);

dy22=q0+cy2*(dt/2);

dy33=y0+cy3*(dt/2);

dy1=(r/w1)-(0.5*i*cx*1.24*exp((-dy33)/7800)*s*pow(dy11,2))/w1-9.81*sin(dy22);

dy2=(-9.81*cos(dy22))/dy11;

dy3=dy11*sin(dy22);

w1=w1-q*dt;

y111=(dt/6)*(ay1+2*(by1+cy1)+dy1);

y222=(dt/6)*(ay2+2*(by2+cy2)+dy2);

y333=(dt/6)*(ay3+2*(by3+cy3)+dy3);

y1=v0+y111;

y2=q0+y222;

y3=y0+y333;

y4=x0+(y333/tan(y2));

printf("v=%f\t",y1); printf("q=%f\t",y2); printf("x=%f\t",y4); printf("y=%f\t",y3);

if(k==1 || k%100==0)

{

fprintf(fin,"%f\t ",y1); fprintf(fin,"%f\t ",y2); fprintf(fin,"%f\t ",y4); fprintf(fin,"%f\t ",y3);

printf(fin,"%f\n ",t0);

}

t0=t0+dt;

if(t0>4)r=0;

v0=y1;

y0=y3;

x0=y4;

q0=y2;

if(t0<=4){ w=m-q*(t0+(dt/2)); w1=m-q*(t0+dt); }

if(t0>4)w1=w=m-q*4;

k++;

if(k==10000) break;

}

while(y3>0);

printf("\n");

printf("RASCHT ZAKONCHEN NAGMITE 'ENTER', FILE RUNGIKUTT.txt");

fclose(fin); getch(); return 0;

}