Решение задачи построения модели для одного шага интегрирования методами Эйлера и Рунге-Кутта Начальные условия

Для решения задачи построения модели расчета траектории неуправляемого летательного аппарата на одном шаг интегрирования системы, определяющей движение ЛА в начале активного участка траектории, методами Эйлера и Рунге - Кутта начальными условиями будут:

• шаг интегрирования h равняется 0.01 с. (h=0.01 с.);

• начальный момент времени

• скорость ЛА в момент схода с направляющих;

• угол наклона направляющих

• начальная абсцисса

• начальная ордината

Расчет системы уравнений методом Эйлера

Рассмотрим уравнения движения в проекциях на касательную и нормаль к траектории:

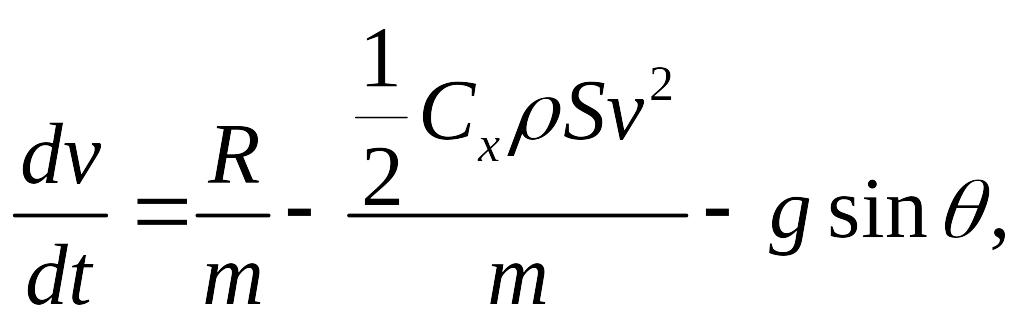(1)

(2)

(3)

(4)

при начальных условиях:

;

Примем за шаг интегрирования с.

По известным начальным условиям определим значения производных _{, , ,} в начальной точке где :

где где

где H=7800 м,

где

где

где

Определим новое значение функций :

Расчет системы уравнений методом Рунге-Кутта

Рассмотрим уравнения движения в проекциях на касательную и нормаль к траектории:

(1)

(2)

(3)

(4)

при начальных условиях:

Примем за шаг интегрирования с.

Пусть где

При :

:

:

:

Будем рассматривать систему трёх дифференциальных уравнений для определения v, θ и y, а x определять после определения v, θ и y.

По известным начальным условиям определим значения производных _{, ,} в начальной точке А, где :

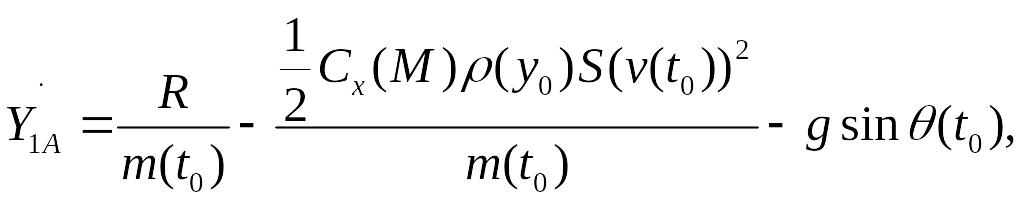
где где

где H=7800 м,

где

где

Из начальной точки A проведём прямую и отметим значение её ординаты в середине шага интегрирования (точка B с координатами ):

где

где

где

Найдём значения производных _{, ,} в точке B:

где где

где H=7800 м,

где

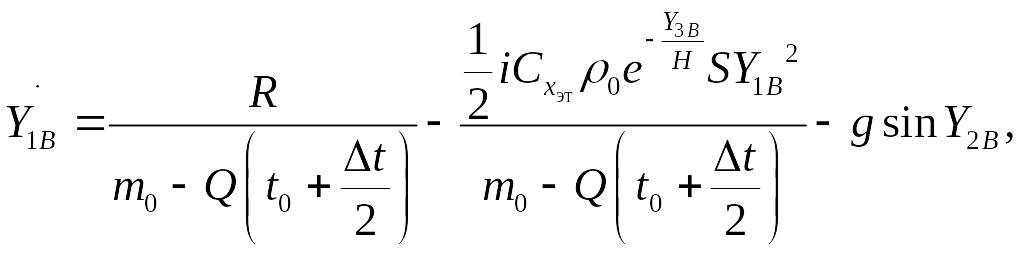
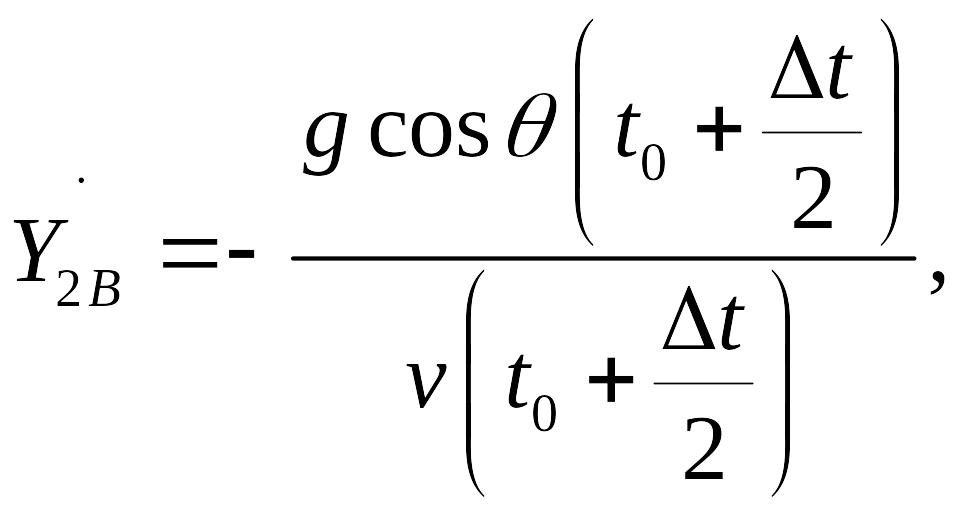
где

Проведём из точки А прямую и отметим значение её ординаты в середине шага интегрирования (точка С с координатами ):

где

где

где

Найдём значения производных _{, ,} в точке С:

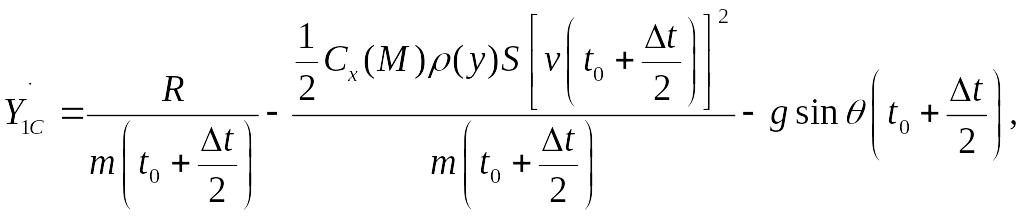
где где

где H=7800 м,

где

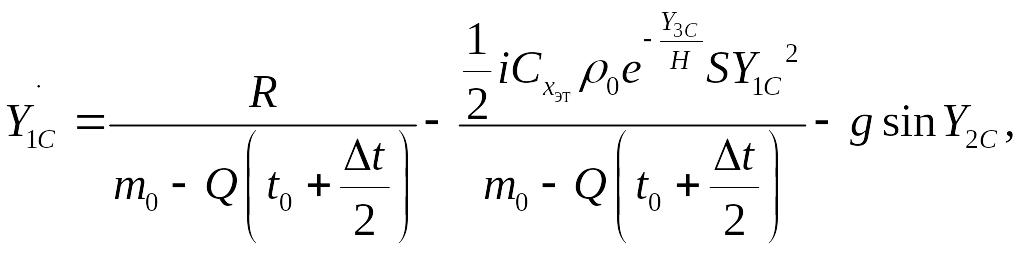
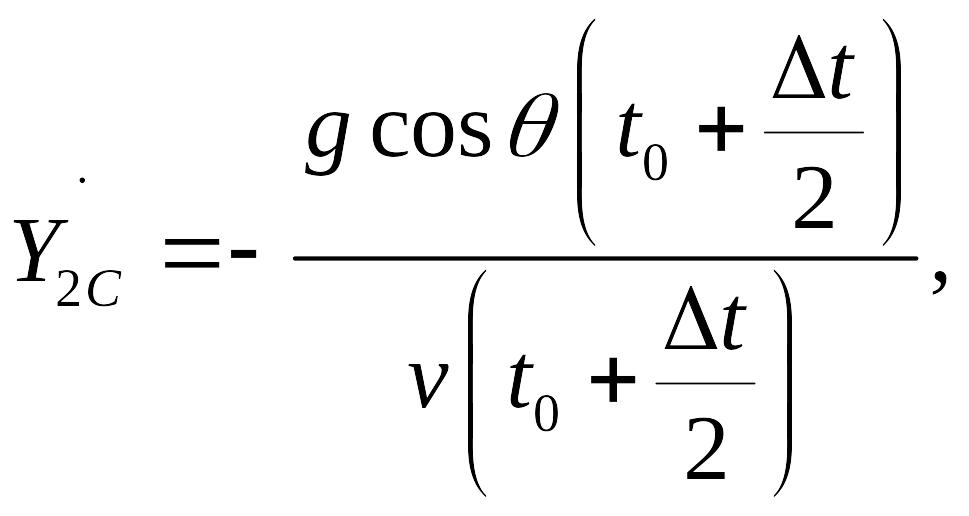
где

Проведём из точки А прямую и отметим значение её ординаты в конце шага интегрирования (точка D с координатами ):

где

где

где

Найдём значения производных _{, ,} в точке D:

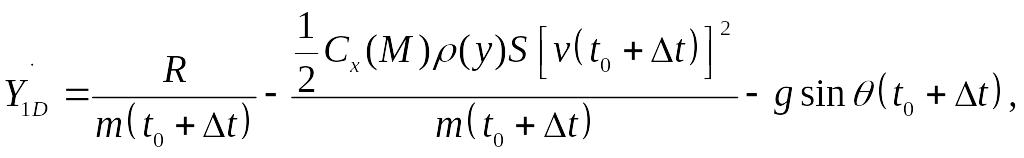
где где

где H=7800 м,

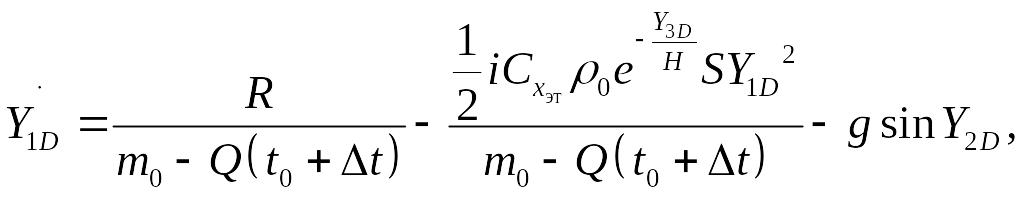
где

где

5. Согласно расчётным формулам метода Рунге-Кутта :

Определим новое значение функций :

где

где

где

Определим новое значение функции

Сравнение решений тестового примера на 1 шаг, полученных без пк

Сравнение результатов производится в соответствии с данными, представленными в таблице 6:

Таблица 6

Обозначения
Ручной счет методом Эйлера	23.749	0.782	1.928	1.928
Ручной счет методом Рунге-Кутта	23.761	0.782	1.931	1.932

Результаты расчета траекторных параметров неуправляемого ЛА

Движение по направляющим

Результатами расчета траекторных параметров данного участка траектории являются значения дульной скорости v_д и дульного времени t_д (см. Таблица 3).

Активный участок траектории ЛА

Расчет траекторных параметров на конце активного участка полета ЛА произведен с помощью программы, написанной на языке программирования С++. Шаг интегрирования 0.01. Входными данными являются параметры движения по направляющим.(см. Таблица 4). Тексты программ и промежуточные значения см. В Приложении.

Пассивный участок траектории ЛА

Расчет траекторных параметров на конце пассивного участка полета ЛА произведен с помощью программы, написанной на языке программирования С++. Шаг интегрирования 0.01. Входными данными являются параметры движения по направляющим.(см. Таблица 5). Тексты программ и промежуточные значения см. В Приложении.

Расчет траектории пассивного участка полета ЛА с использованием параболической теории

Параболическая теория изучает движение тяжелой материальной точки в пустоте в стационарном однородном параллельном поле земного тяготения. Теорию применяют для ориентировочного расчета траектории ЛА, имеющих больших высотах и малую скорость полета, и для расчета траектории ЛА на больших высотах, где сила сопротивления ничтожна мала. Возможность получения аналитического выражения траектории позволяет найти выражения для коэффициентов чувствительности, которые являются частными производными от дальности по соответствующим параметрам.

,

,

.

где t₀=0.2202

y₀=y_а=552.59 м,

x₀=x_а=789.37 м,

v₀=v_а=432 м/с,

0.574,

м/с.

(параметры конца активного участка рассчитанные по данным расчёта методом Рунге - Кутта).

Для вершины траектории время вычисляется по формуле:

Подставляя t в вышеуказанные зависимости, получим, что

x(t)=789.37+363.082*23.941=9482 м,

y(t)=552.59+234.861*23.941-(9.81*23.941²)/2=3364 м.

Для точки конца траектории (точки падения) имеем y(t)=0. Тогда

м.,