Программа рассчета методом Рунге-Кутта:

Метод Рунге-Кутта:

function F = rparts2(t,y,R)

V = y(1);

TT = y(2);

g = 9.81;

S=0.0346;

i=1.8;

Cxet=0.157;

Cx=i*Cxet;

r0=1.23*exp(-1.414/7800);

X = Cx*r0*V^2/2*S;

m0start = 110;

empty_mass = 92;

timeDU = 1.8;%время горения топлива

Q = (m0start - empty_mass)/timeDU;

if(R>0)

m = m0start - Q*t;

else

m = empty_mass;

end

F(1) = (R - X - m*g*sin(TT))/m;

F(2) = -g*cos(TT)/V;

F(3) = V*cos(TT);

F(4) = V*sin(TT);

F=F';

end

Исполнительный файл:

opt1=odeset('Reltol',0.01);

t0=0.17;

g = 9.81;

R = 20000;

Ttopl = 1.8;

y0 = [29.482 0.785 1.414 1.414];

ta=Ttopl-t0;

rparts(t0,y0,R);

[Ta1,ResA1] = ode45(@(t,y) rparts(t,y,R),[t0,ta],y0,opt1);

Za1 = ResA1(end, :)

[Tp1,ResP1] = ode45(@(t,y) rparts(t,y,0),[ta Tp(end)+0.07],Za1,opt1);

Промежуточные результаты:

27.7149 0.7854 1.4142 1.4142

28.4254 0.7845 1.4862 1.4861

29.1362 0.7836 1.5601 1.5598

29.8473 0.7828 1.6358 1.6353

30.5586 0.7819 1.7135 1.7124

138.8086 0.7280 34.9649 32.2723

148.4420 0.7256 39.9442 36.6998

158.1175 0.7234 45.2689 41.4126

167.8350 0.7213 50.9414 46.4114

177.5942 0.7193 56.9635 51.6967

187.3950 0.7175 63.3375 57.2689

349.6270 0.6961 214.7064 185.9746

360.0889 0.6951 227.3440 196.5249

413.5883 0.6905 297.2397 254.5340

419.2521 0.6901 305.1513 261.0678

424.9252 0.6897 313.1735 267.6871

1.0e+004 *

0.0425 0.0001 0.0313 0.0268

0.0424 0.0001 0.0329 0.0281

0.0423 0.0001 0.0345 0.0294

0.0422 0.0001 0.0360 0.0306

0.0265 0.0000 0.3618 0.2377

0.0255 0.0000 0.3903 0.2488

0.0246 0.0000 0.4183 0.2583

0.0238 0.0000 0.4456 0.2662

0.0230 0.0000 0.4724 0.2726

0.0236 -0.0001 0.9705 0.0648

0.0239 -0.0001 0.9835 0.0481

0.0242 -0.0001 0.9963 0.0309

0.0246 -0.0001 1.0089 0.0132

0.0249 -0.0001 1.0213 -0.0049

Выводы по проделанной работе

В ходе выполнения курсового проекта была построена математическая модель неуправляемого реактивного снаряда с учетом следующих допущений:

• Реактивная сила R равна нулю(R=0).

• Поверхность Земли представляется в виде бесконечной плоскости.

• Коэффициент сопротивления Cx считается постоянным на всей траектории полета снаряда.

• Масса ЛА при движении по направляющим и на пассивном участке постоянна( ).

• Шаг интегрирования был взят .

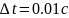По построенной математической модели была создана компьютерная модель полета снаряда, которая заключалась в написании программ реализующих методы численного интегрирования (Эйлера и Рунге-Кутта). В ходе вычислений были получены близкие результаты параметров полета снаряда.

Метод Рунге-Кутта показал большую точность, так как он аппроксимирует участки траектории кривыми второго порядка, что является более точным методом. По методу Эйлера были получены чуть меньшие данные по дальности, чем по методу Рунге-Кутта. Погрешность метода Эйлера больше, чем метода Рунге-Кутта, но этот метод значительно проще по расчетам.

Был также произведен расчет по параболической теории. В результате расчета была получена дальность, чуть большая, чем дальности полученные методами численного интегрирования, но все же близкие к ним.

В исследовательской части было произведено изучение влияния входных данных на выходные данные движения ЛА. Этими выходными данными являются: ускорение свободного падения, коэффициент сопротивления Cx и шаг интегрирования 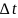. Было получено, что точность ввода ускорения свободного падения практически не влияет на дальность полета ЛА; при уменьшении Cx также не было получено существенных отличий в дальности, но при увеличение значения Cx были получены меньшие значения дальности. Уменьшение шага интегрирования в 2 раза не дало существенных изменений параметров ЛА, зато увеличение в 2 раза дало увеличение в дальности на 300-400 метров. Также можно заметить из таблицы 8, что значения дальности, полученные методом Эйлера при шаге интегрирования и методом Рунге-Кутта при шаге 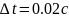практически равны.