1.13. Построение характеристик замкнутой системы уп-д с отрицательной обратной связью по скорости

Уравнение электромеханической характеристики системы:

(55)

где к - коэффициент усиления ТП (равен 100 по заданию), к_ос - коэффициент обратной связи по скорости, r_∑ = 3r_а = 3∙0,328 = 0,984 Ом.

По заданию необходимо подобрать к_ос таким, чтобы жесткость замкнутой системы была в 10 раз выше, чем на естественной характеристике.

Значение к_ос находим из выражения:

.

Для определения величины используем условие прохождения характеристики через номинальную точку .

Структурная схема замкнутой системы ТП-Д с обратной связью по скорости представлена на рис. 26. Характеристика замкнутой системы и естественная электромеханическая характеристика приведены на рис. 27.

Рис. 26. Структурная схема замкнутой системы ТП-Д с обратной связью по скорости

Рис. 27. Характеристика замкнутой системы и естественная электромеханическая характеристика

1.14. Демпфирующая способность электропривода

Двухмассовая электромеханическая система с упругими связями описывается системой дифференциальных уравнений:

, (61) (56)

где М_кз = кФ_нI_кз = кФ_нU_н/r – момент короткого замыкания; b = (кФ_н)²/r – жесткость механической характеристики. Переходные процессы в такой системе носят колебательный характер, однако, электропривод благодаря наличию упругой механической связи оказывает на колебания демпфирующее действие.

Структурная схема двухмассовой ЭМС представлены на рис. 28.

Рис. 28. Структурная схема двухмассовой ЭМС

График переходного процесса в неоптимизированной ЭМС (при естественных параметрах модели) представлен на рис. 29. По нему видно, что при неоптимизированных параметрах электропривод очень слабо демпфирует колебания.

Для улучшения демпфирующей способности электропривода сначало найдем оптимальную жесткость механической характеристики, при которой время переходного процесса будет минимально. При введении добавочного сопротивления в цепь якоря, демпфирующая способность привода до некоторого значения сопротивления r_{доб.опт.} будет возрастать, а после – опять уменьшаться. Графики переходных процессов при различных r_доб. представлены на рис. 30, рис. 31, рис. 32 и рис. 33.

Далее для оптимизации переходного процесса исследуем влияние γ на демпфирующую способность. Графики переходных процессов при различных значениях γ представлены на рис. 34, рис. 35, рис. 36 и рис. 37.

Далее для оптимизации переходного процесса исследуем влияние Ω на демпфирующую способность. Графики переходных процессов при различных значениях Ω представлены на рис. 38, рис. 39, рис. 40 и рис. 41.

Так же исследуем влияние индуктивности якоря на демпфирующую способность электропривода. Для этого увеличим в модели индуктивность якоря в 10 и 30 раз. Графики переходных процессов при увеличении индуктивности якорной цепи представлены на рис. 42 и рис. 43.

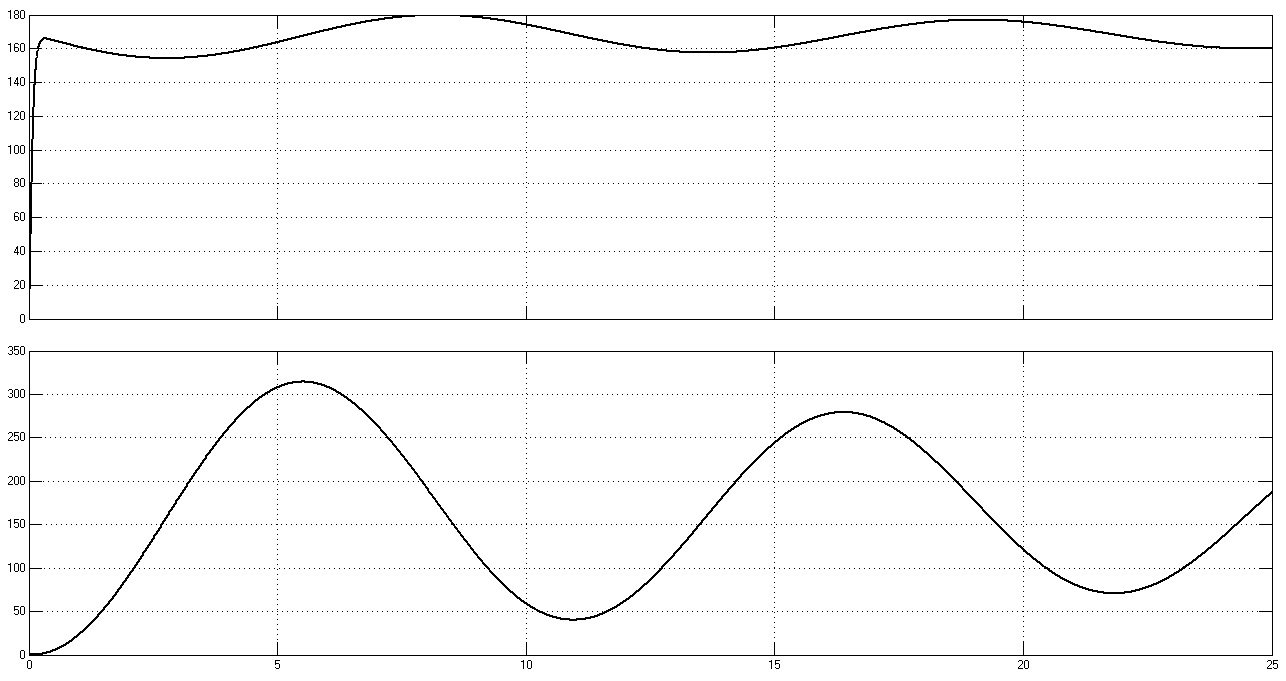
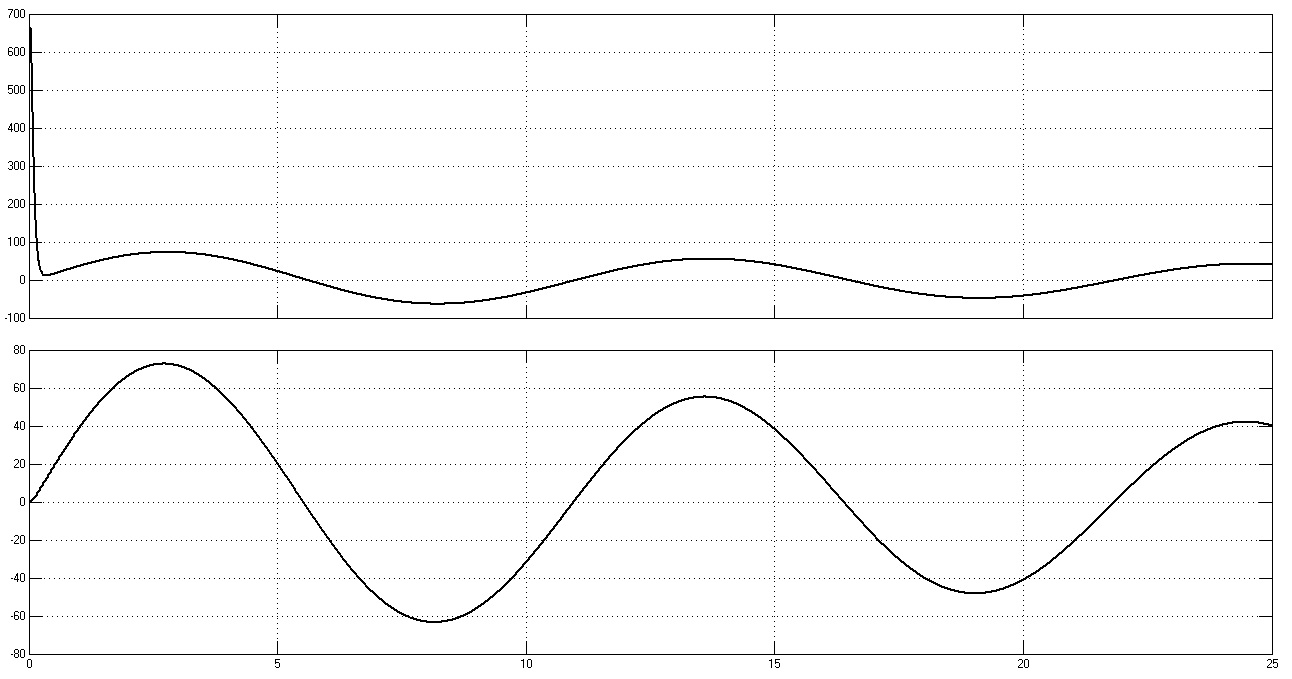
Рис. 29. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) в неоптимизированной системе

Рис. 30. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при r_доб = 5r_я

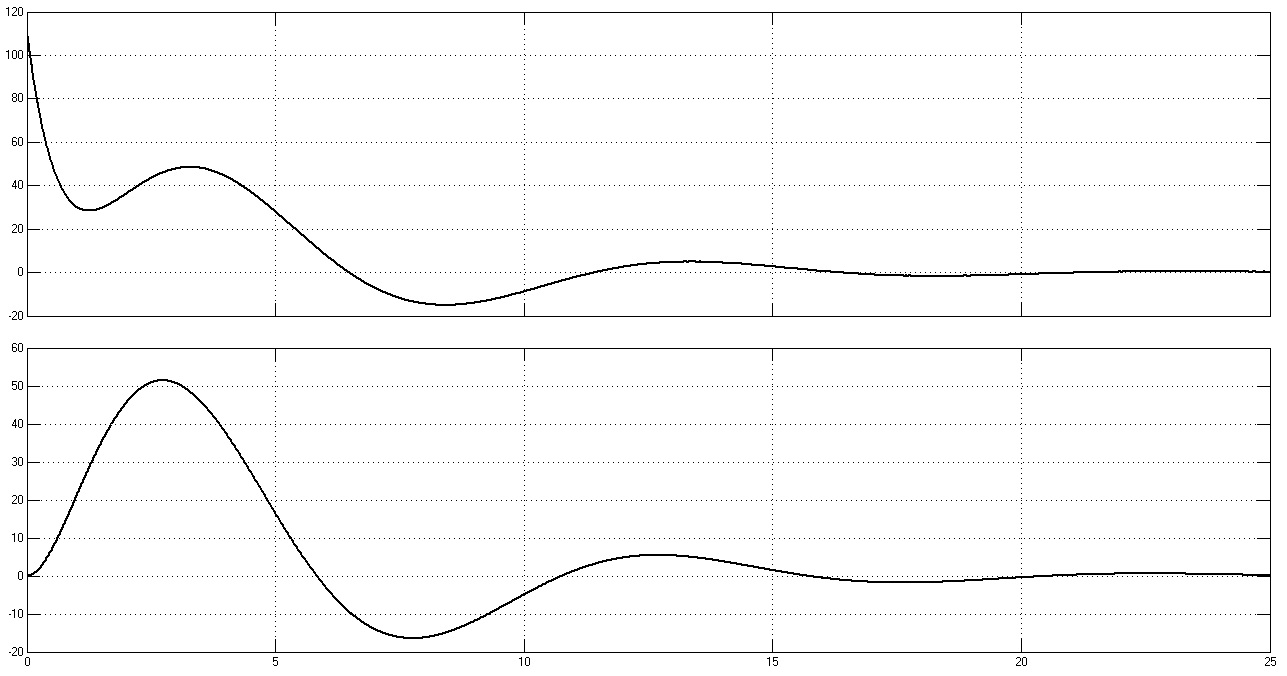
Рис. 31. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при r_доб = 7r_я

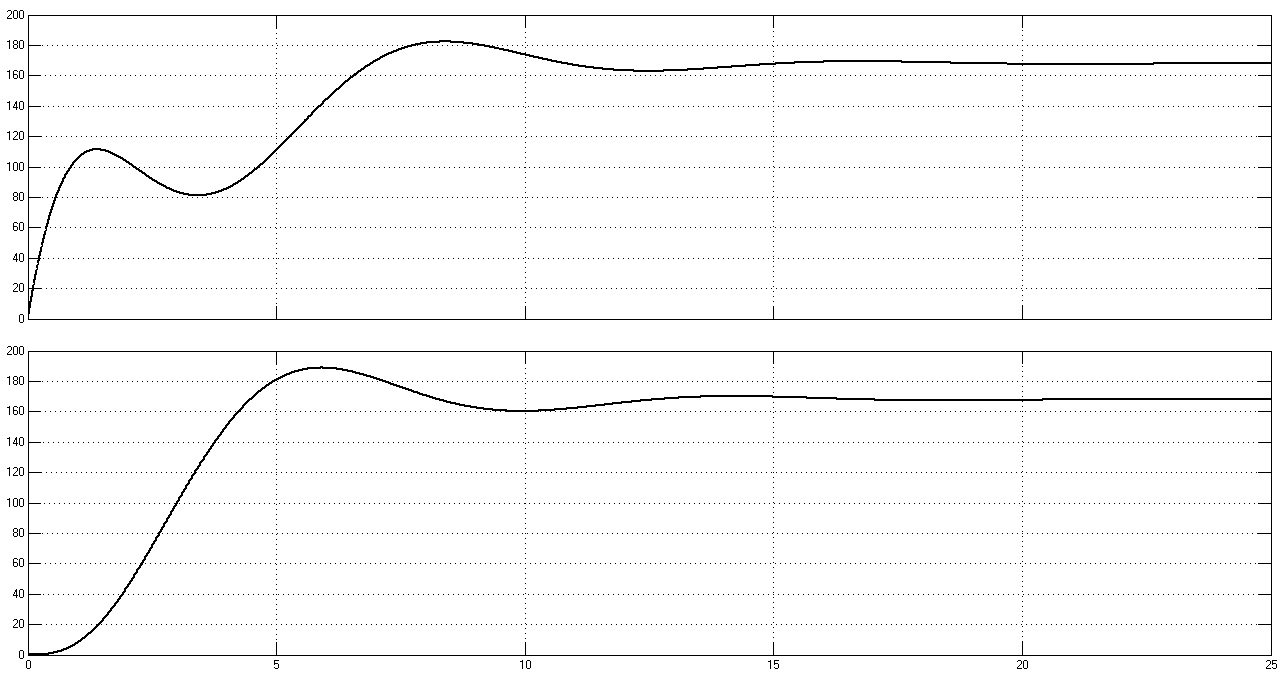
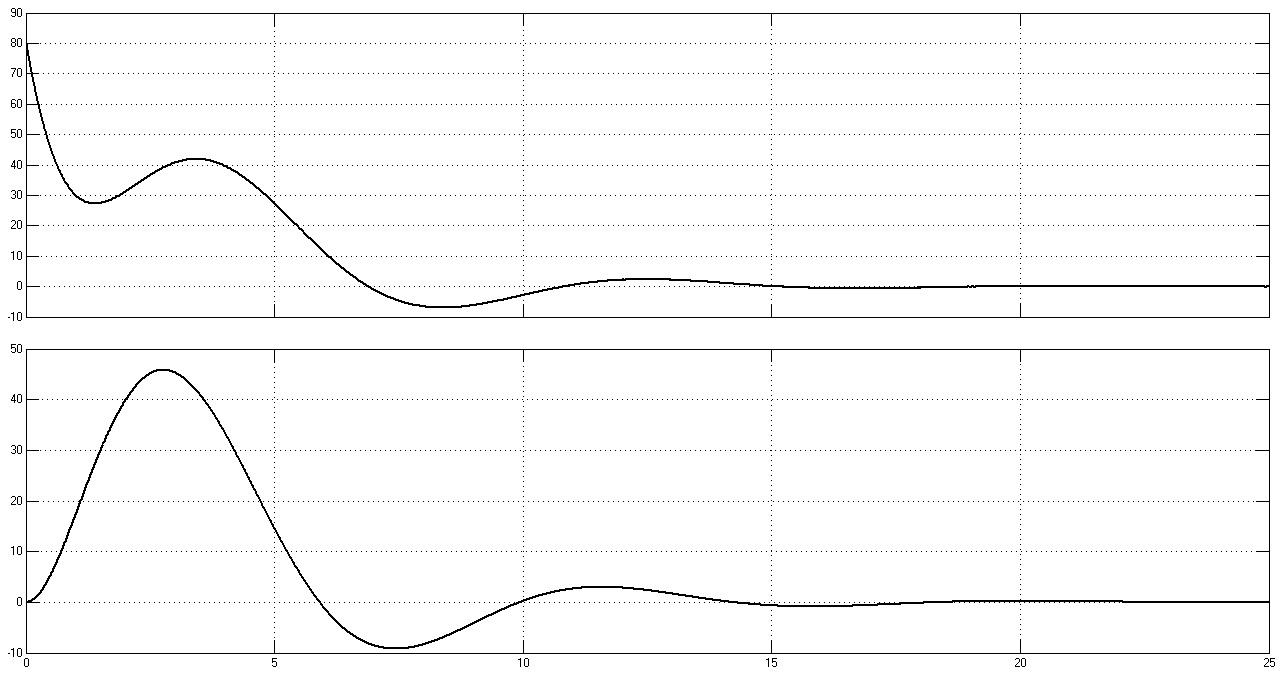
Рис. 32. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t)

при r_доб = 10r_я

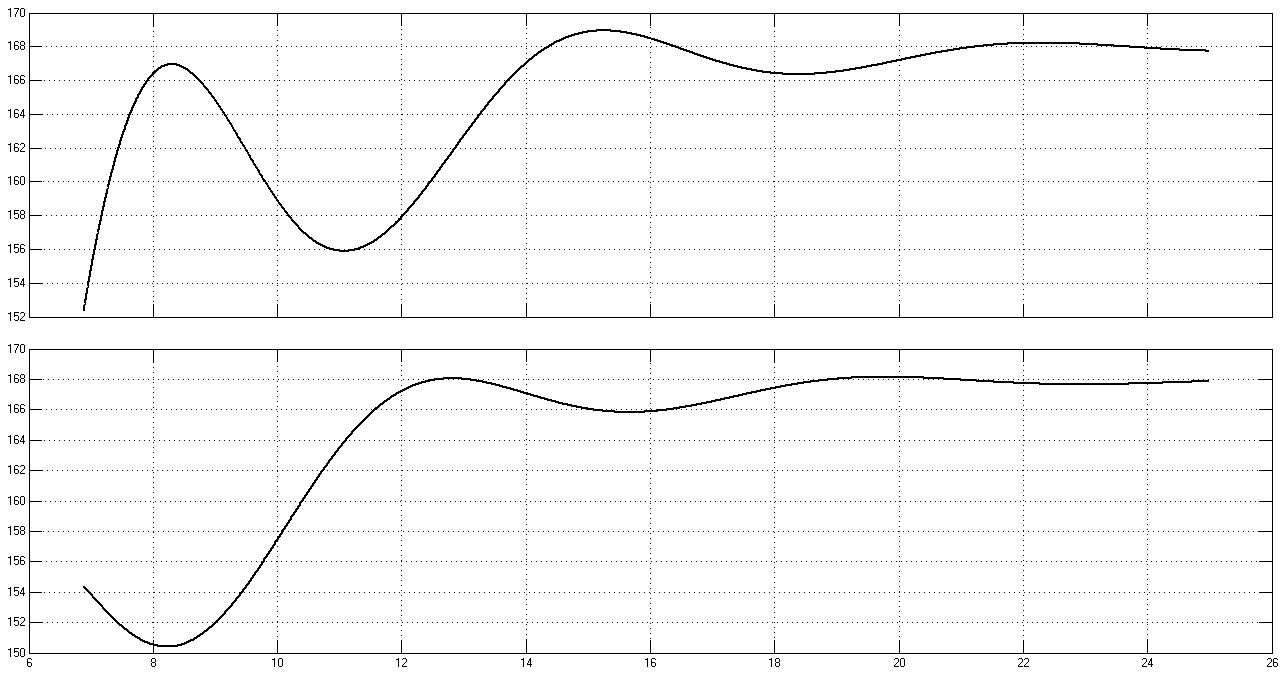
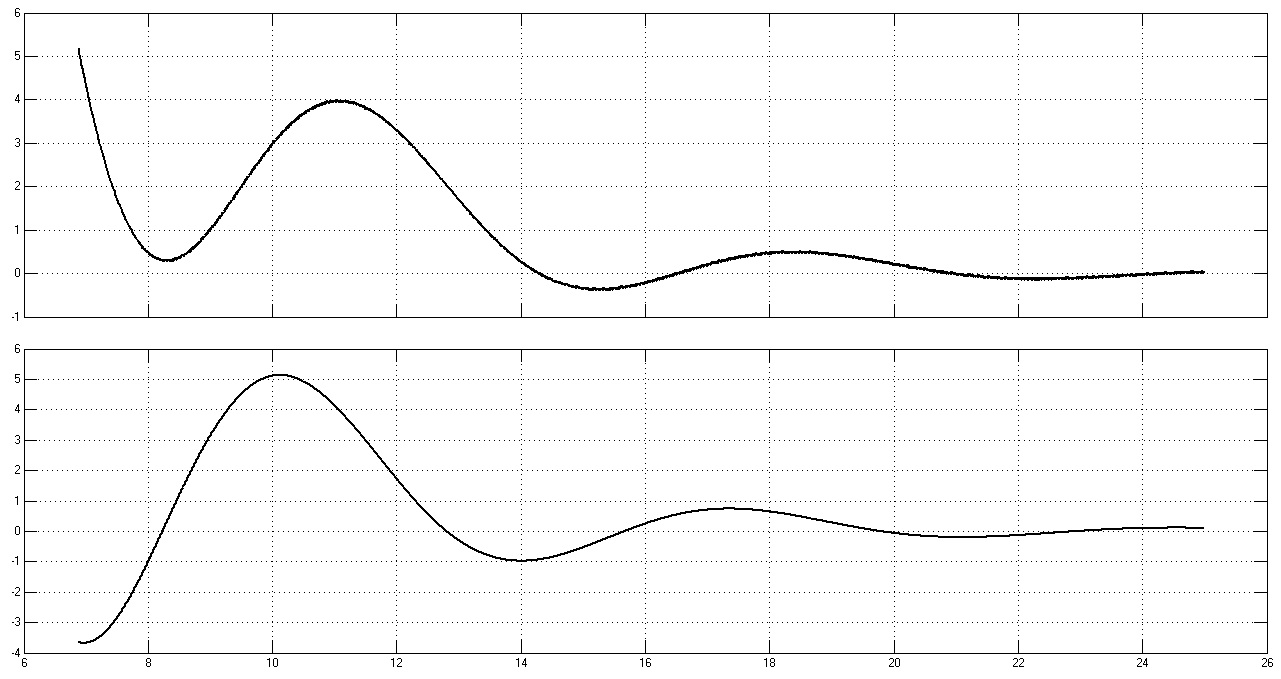
Рис. 33. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t)

при r_доб = 15r_я

Рис. 34. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при γ = 2,5

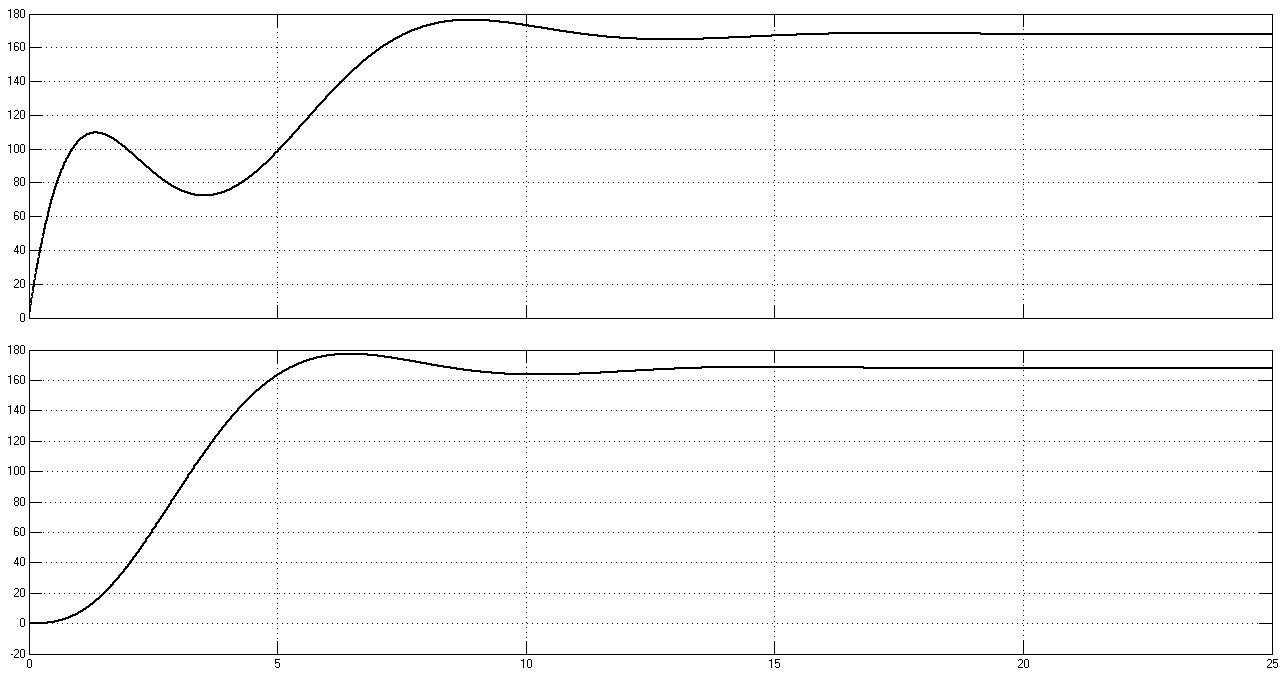
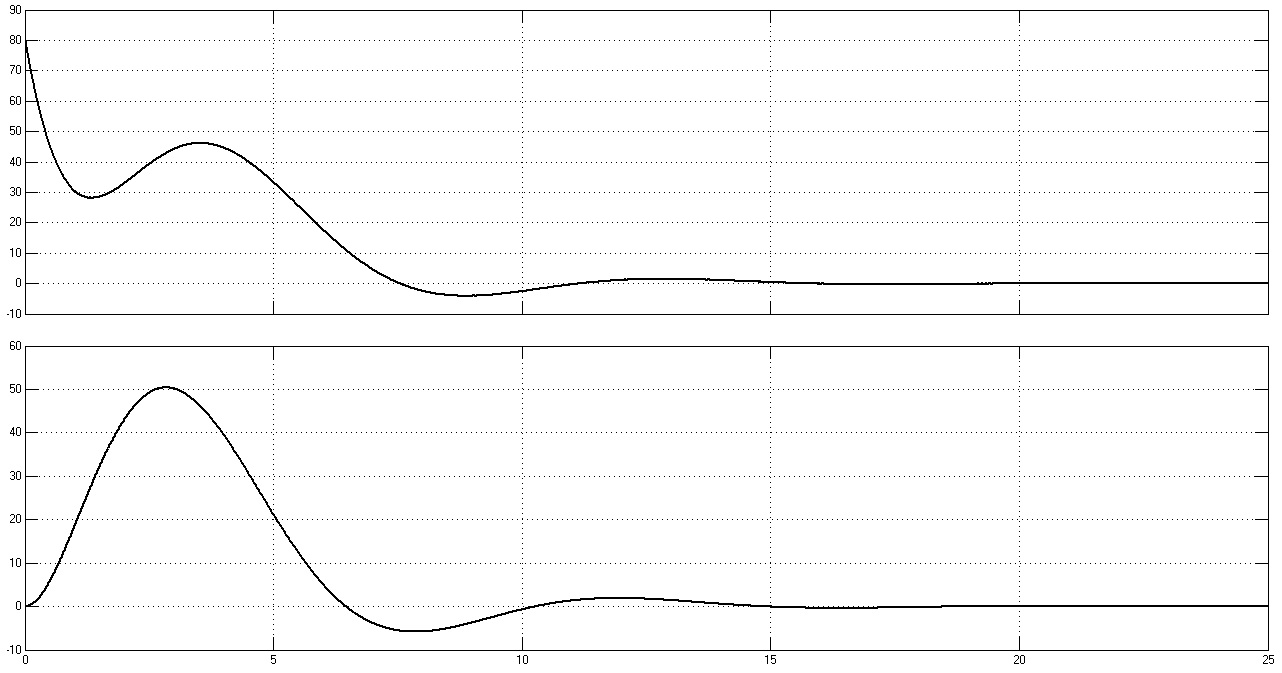
Рис. 35. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при γ = 3,5

Рис. 36. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при γ = 4

Рис. 37. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при γ = 5

Рис. 38. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при Ω = 1,3

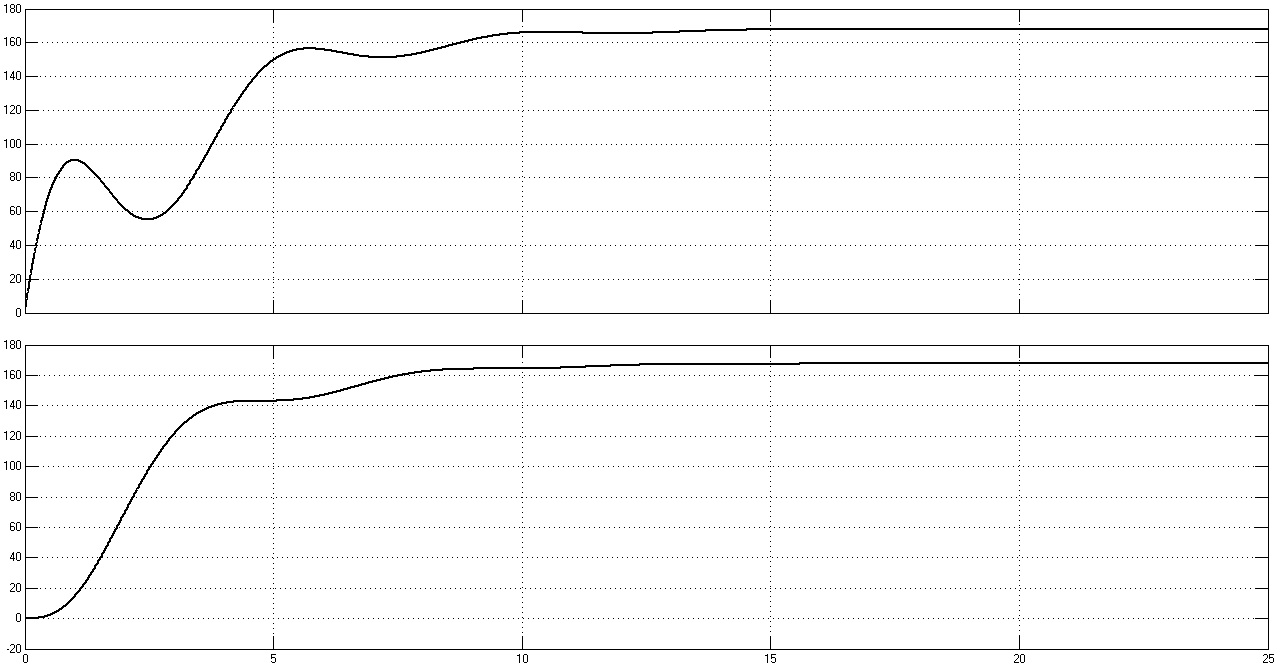
Рис. 39. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при Ω = 1,5

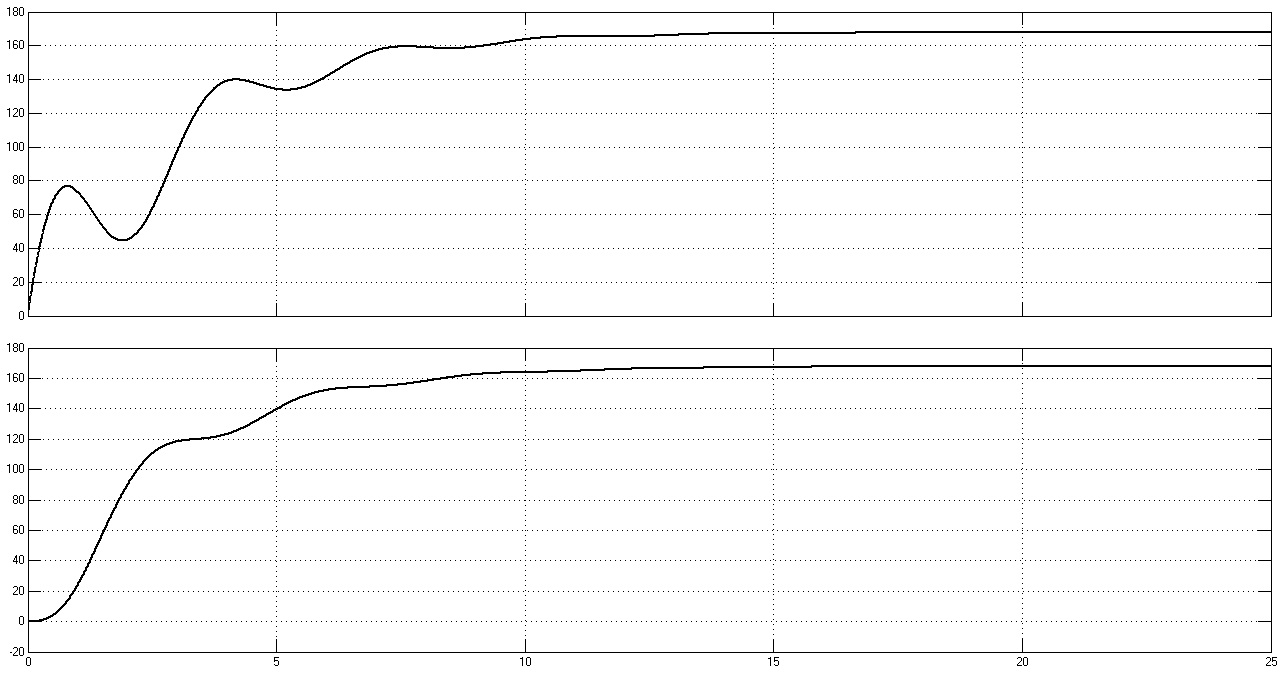
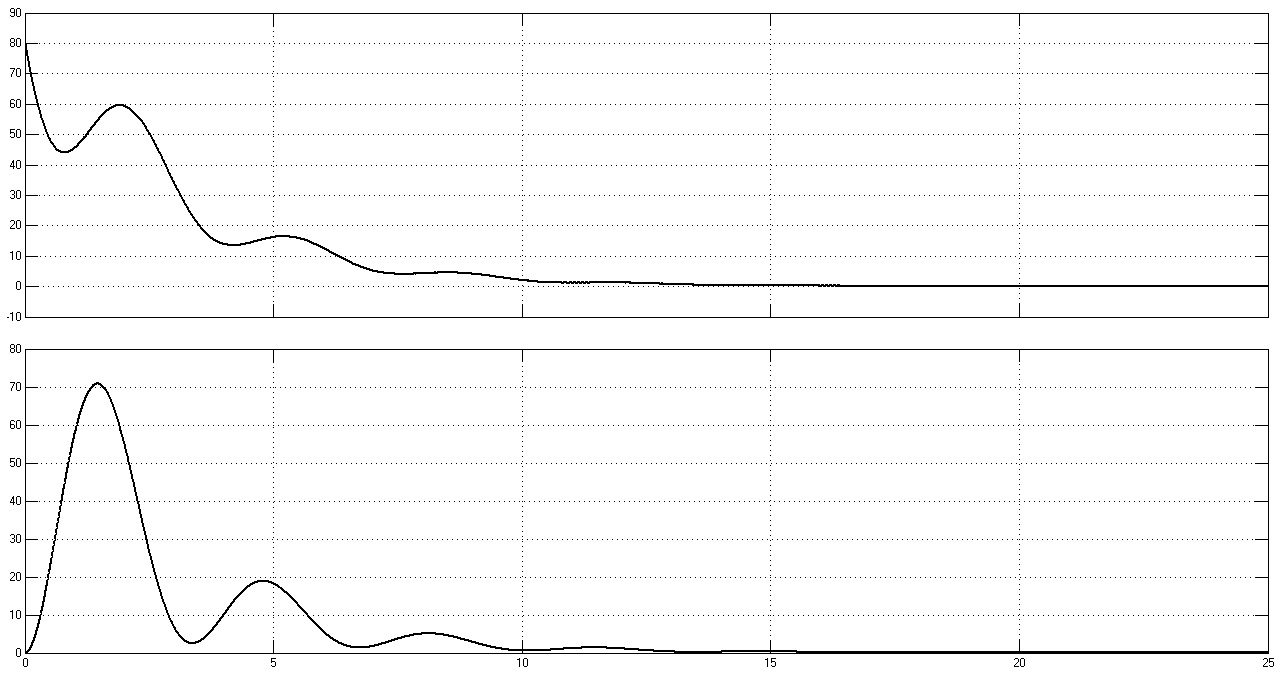
Рис. 40. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при Ω = 2

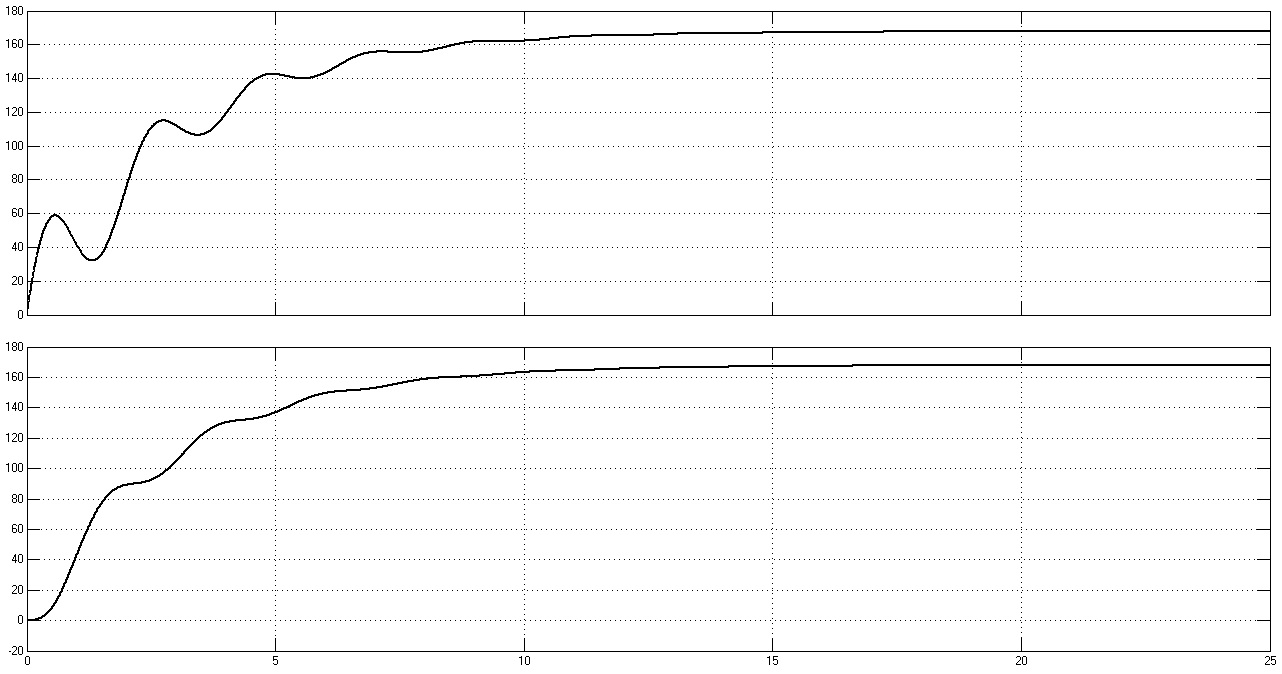
Рис. 41. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t) при Ω = 3

Рис. 42. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t)

при L = 10L_я

Рис. 43. Графики переходных процессов w₁(t), w₂(t), M(t) и M₁₂(t)

при L = 30L_я

Как видно из графиков оптимальному переходному процессу соответствуют следующие параметры: r_{доб.опт.} = 10r_я, γ_опт = 3,5, Ω_опт = 1,5 Гц. Также из графиков следует, что увеличение индуктивности цепи якоря исследуемого двигателя не сказывается на времени переходного процесса.