1.8. Сброс и наброс нагрузки

Построение переходных процессов =f(t) и I=f(t) с учетом индуктивности якоря при набросе нагрузки с M_c1 = 0 до M_c2 = М_н и при сбросе с M_c2 = М_н до M_c1 = 0 для реальных параметров выбранного двигателя.

Наброс нагрузки с M_c1 = 0 до M_c2 = М_н

4Т_Я <Т_М , следовательно процесс апериодический.

Для получения колебательного процесса увеличим индуктивность якоря в 10 раз.

4Т_Я >Т_М , следовательно процесс колебательный.

Сброс нагрузки с M_c2 = М_н до M_c1 = 0

Зависимости , M(t) и I(t) представлены на рис. 16, рис. 17 и рис. 19. Динамические механические характеристики представлены на рис. 18 и рис. 20.

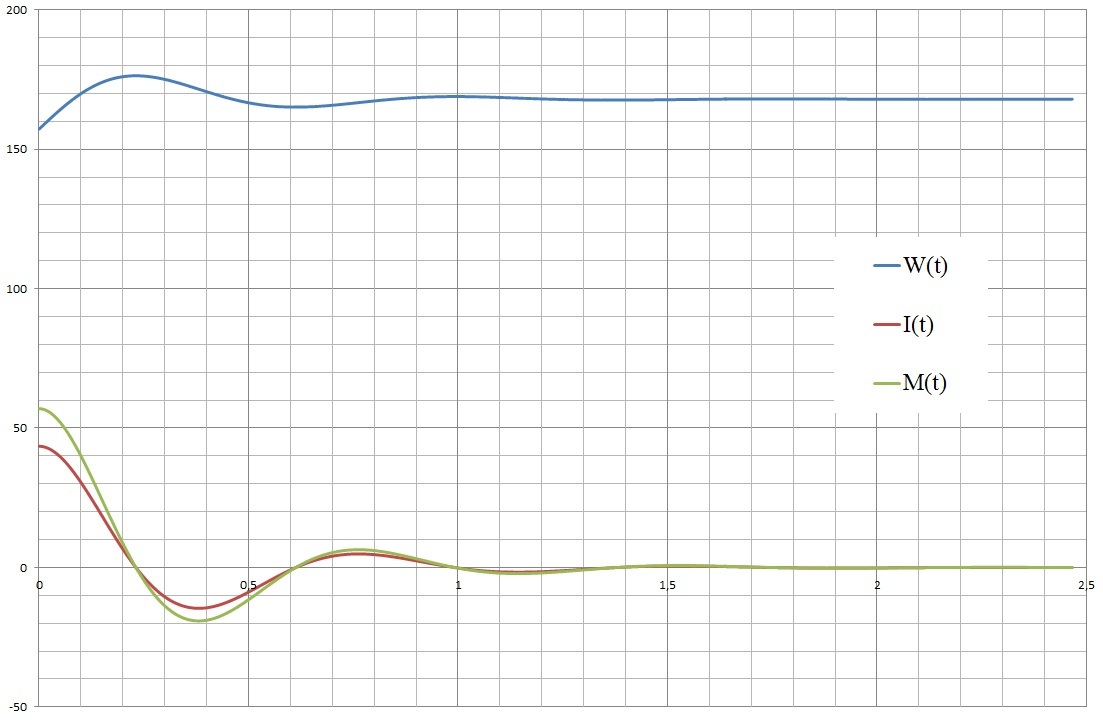
Рис. 16. Зависимости , M(t) и I(t) при сбросе нагрузки (колебательный процесс)

Рис. 17. Зависимости , M(t) и I(t) при набросе нагрузки (колебательный процесс)

Рис. 18. Динамическая механическая характеристика при набросе – сбросе нагрузки (колебательный процесс)

Рис. 19. Зависимости , M(t) и I(t) при набросе – сбросе нагрузки (апериодический процесс)

Рис. 20. Динамическая механическая характеристика при набросе – сбросе нагрузки (апериодический процесс)

1.9. СТРУКТУРНАЯ СХЕМА ДВУХМАССОВОЙ ЭМС МЕХАНИЗМА

ПЕРЕДВИЖЕНИЯ ТЕЛЕЖКИ

Рис. 21. Структурная схема двухмассовой ЭМС

Уравнение АЧХ –

(41)

На рис. 22 представлена АЧХ двухмассовой ЭМС.

Рис. 22. АЧХ двухмассовой ЭМС

1.10. РАСЧЕТ И ПОСТРОЕНИЕ МЕХАНИЧЕСКИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ ДЛЯ ПУСКА ДВУХМАССОВОЙ ЭМС

Момент упругой связи –

(42)

где

. (43)

Скорость 1-ой массы –

; (44)

Скорость 2-ой массы –

. (45)

Графики упругого момента и скоростей первой и второй масс при М_с = 0 представлены на рис.22-23.

Рис. 22. График упругого момента при пуске М_с=0

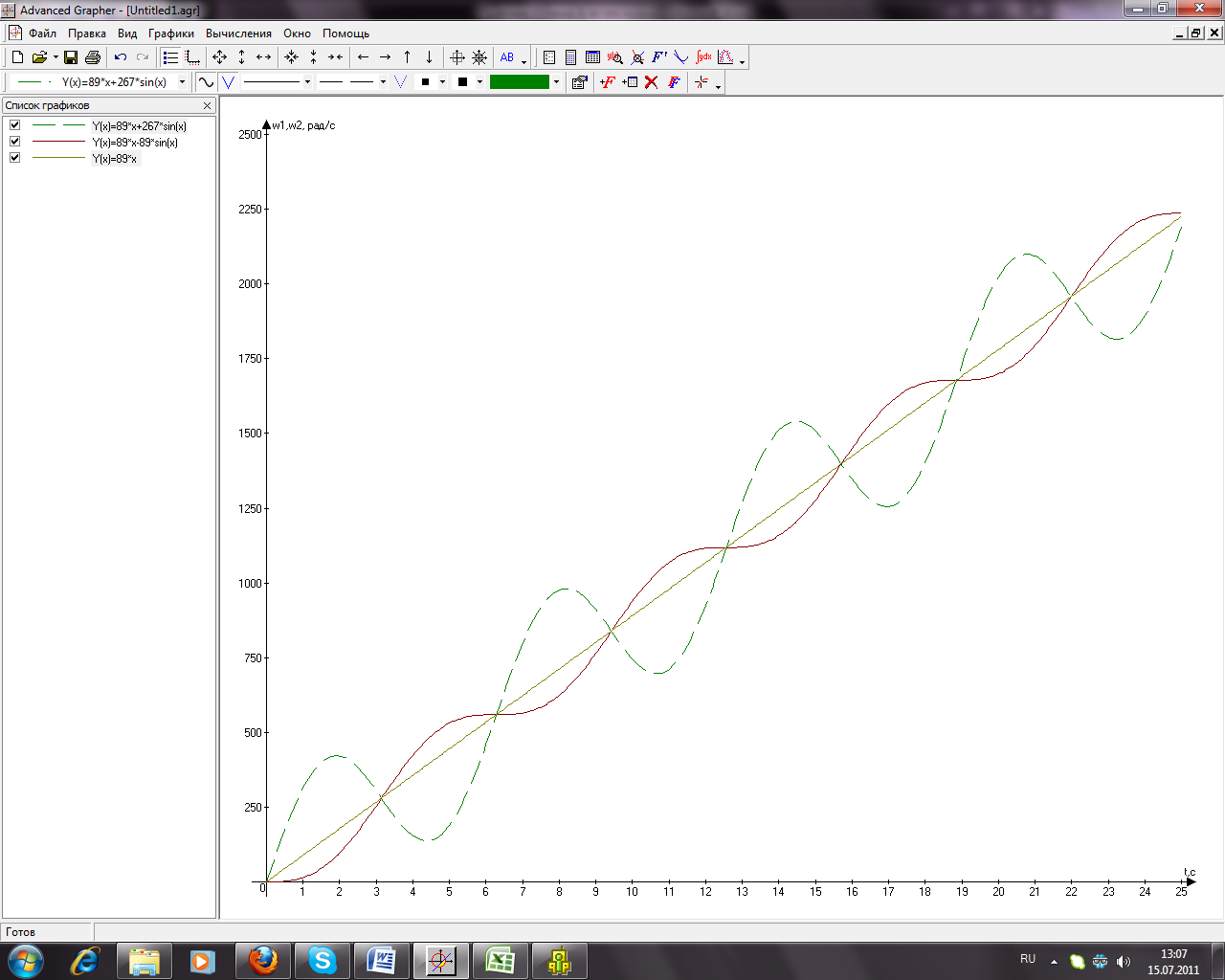
Рис. 23. Графики скоростей 1 и 2 массы при пуске М_с=0

1.11. ПОСТРОЕНИЕ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК В РАЗОМКНУТОЙ СИСТЕМЕ УП-Д

При -

; (46)

Электромеханические характеристики в системе УП-Д представлены на

рис. 24.

Рис. 24. Электромеханические характеристики в системе УП-Д

1.12. Расчет переходных процессов в системе уп-д в режимах пуска, реверса и торможения

Расчет и построение графиков переходных процессов w=f(t), M=f(t) в системе УП-Д в режимах пуска до e_пн =220 В, реверса до -e_пн и торможения при известных M_c=М_н, J_S = J_дв.

Задание на скорость изменяется по линейному закону: w₀(t) = et. Поэтому величину ^½e^½ выбираем из условия пуска: e = (М_макс - M_c)/J_S. При расчетах реверса и торможения можно принять ^½e_р^½=^½e_т^½=^½e_п^½. Момент статический по заданию принимаем реактивным и равным М_н.

1) Пуск

1 участок:

(47)

2 участок:

(48)

3 участок:

ω_С = 146,49 (1/с); ω_нач = 92,46 (1/с);

М_С = 38 (Н м); М_нач = 133,76 (Н м).

(49)

2) Реверс

1 участок:

(50)

2 участок:

(51)

3 участок:

ω_С = -146,49 (1/с); ω_нач = -79,95 (1/с);

М_С = -38 (Н м); М_нач = -155,95 (Н м).

(52)

3) Торможение

1 участок:

(53)

2 участок:

ω_С = 0 (1/с); ω_нач = -33,64 (1/с);

М_С = 0 (Н м); М_нач = 59,62 (Н м).

(54)

Зависимости w = f(t), M = f(t) и w₀ = f(t) представлены на рис. 24. Динамические механические характеристики представлены на рис. 25.

Рис. 24. Зависимости w = f(t), M = f(t) и w₀ = f(t) для системы УП-Д

Рис. 25. Динамическая механическая характеристика для системы УП-Д